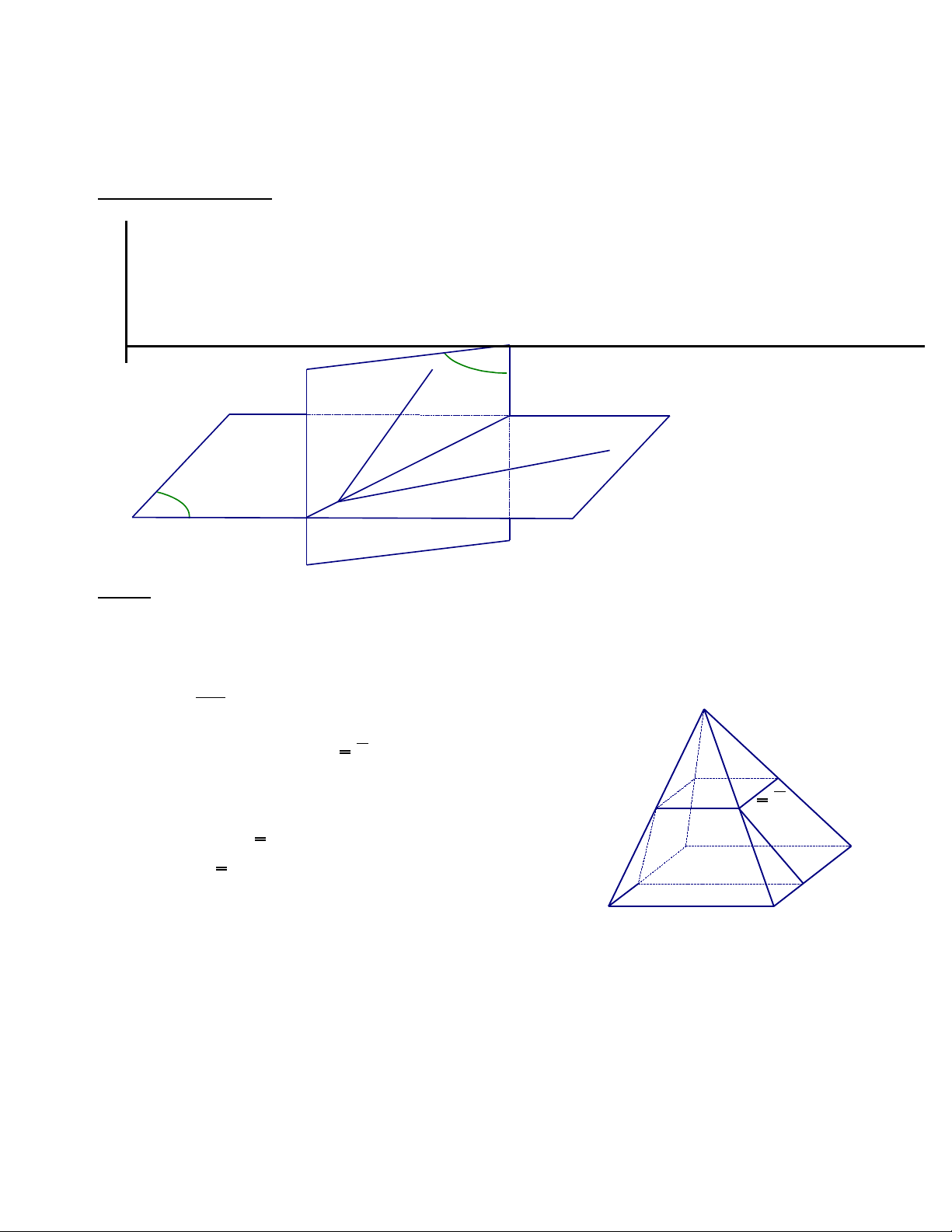
§1 .HAI ĐNG TH NG SONG SONG ƯỜ Ẳ
: Ch ng minh hai đng th ng a và b song song : ứ ườ ẳ
S d ng m t trong các cách sauử ụ ộ :
Ch ng minh a và b đng ph ng và không có đi m chung ứ ồ ẳ ể
Ch ng minh a và b phân bi t và cùng song song v i đng th ng th ba ứ ệ ớ ườ ẳ ứ
Ch ng minh a và b đng ph ng và áp d ng các tính ch t c a hình h c ph ng (c nh đi c a hình ứ ồ ẳ ụ ấ ủ ọ ẳ ạ ố ủ
bình hành , đnh lý talet … )ị
S d ng các đnh lý ử ụ ị
Ch ng minh b ng ph n ch ng ứ ằ ả ứ
a
A
b
Bài t p ậ :
1. Cho hình chóp S.ABCD v i đáy ABCD là hình bình hành .G i A’ ,B’ , C’ ,D’ l n l t là trungớ ọ ầ ượ
đi m các c nh SA , SB , SC , SD .ể ạ
a. Ch ng minh A’B’C’D’ là hình bình hành ứ
b. G i M là đi m b t kì trên BC . Tìm thi t di n c a (A’B’M) v i hình chóp S.ABCDọ ể ấ ế ệ ủ ớ
Gi iả
a. Ch ng minh A’B’C’D’ là hình bình hành ứ:
Trong tam giác SAB, ta có : A’B’
//
2
1
AB
Trong tam giác SCD, ta có : C’D’
//
2
1
CD
M t khác AB ặ
//
CD
A’B’
//
C’D’
V y : A’B’C’D’ là hình bình hànhậ
b. Tìm thi t di n c a (A’B’M) v i hình chóp S.ABCDế ệ ủ ớ :
Ta có : AB ⁄ ⁄ A’B’ và M là đi m chung c a (A’B’M) và (ABCD)ể ủ
Do đó giao tuy n c a (A’B’M) và (ABCD) là Mx ế ủ song song AB và A’B’
G i N = ọMx AD
V y : ậthi t di n là hình thang A’B’MNế ệ
2. Cho hình chóp S.ABCD v i đáy ABCD là hình thang v i c nh đáy AB và CD (AB ớ ớ ạ CD).
G i M , N l n l t là trung đi m các c nh SA , SB ọ ầ ượ ể ạ
a. Ch ng minh : MN ứ⁄ ⁄ CD
N
M
S
A
B
C
A'
B'
C'
D'
b. Tìm P = SC (ADN)
I
S
B
C
M
N
P
A
c. Kéo dài AN và DP c t nhau t i I .ắ ạ
Ch ng minh : SI ứ⁄ ⁄ AB ⁄ ⁄ CD . T giác SABI là hình gì ?ứ
Gi iả
a. Ch ng minh : MN ứ⁄ ⁄ CD :
Trong tam giác SAB, ta có : MN ⁄ ⁄ AB
Mà AB ⁄ ⁄ CD ( ABCD là hình thang )
V y : ậMN ⁄ ⁄ CD
b. Tìm P = SC
(ADN):
Ch n mp ph (SBC) ọ ụ SC
Tìm giao tuy n c a (SBC ) và (ADN)ế ủ
Ta có : N là đi m chung c a (SBC ) và (ADN)ể ủ
Trong (ABCD), g i E = AD ọ AC
( SBC) (ADN ) = NE
Trong (SBC), g i P = SC ọ NE
V y : P = SC ậ ( ADN )
c. Ch ng minh : SI //ứ AB // CD . T giác SABI là hình gì ?ứ
Ta có :
CDABSI
SCD
SAB
SCD
////
CD / / AB
)( CD
)( AB
)( (SAB) SI
( theo đnh lí 2)ị
Xét ASI , ta có : SI // MN ( vì cùng song song AB)
M là trung đi m ABể
SI
//
2MN
Mà AB
//
2.MN
Do đó : SI
//
AB
V y : tậ giác SABI là hình bình hành ứ
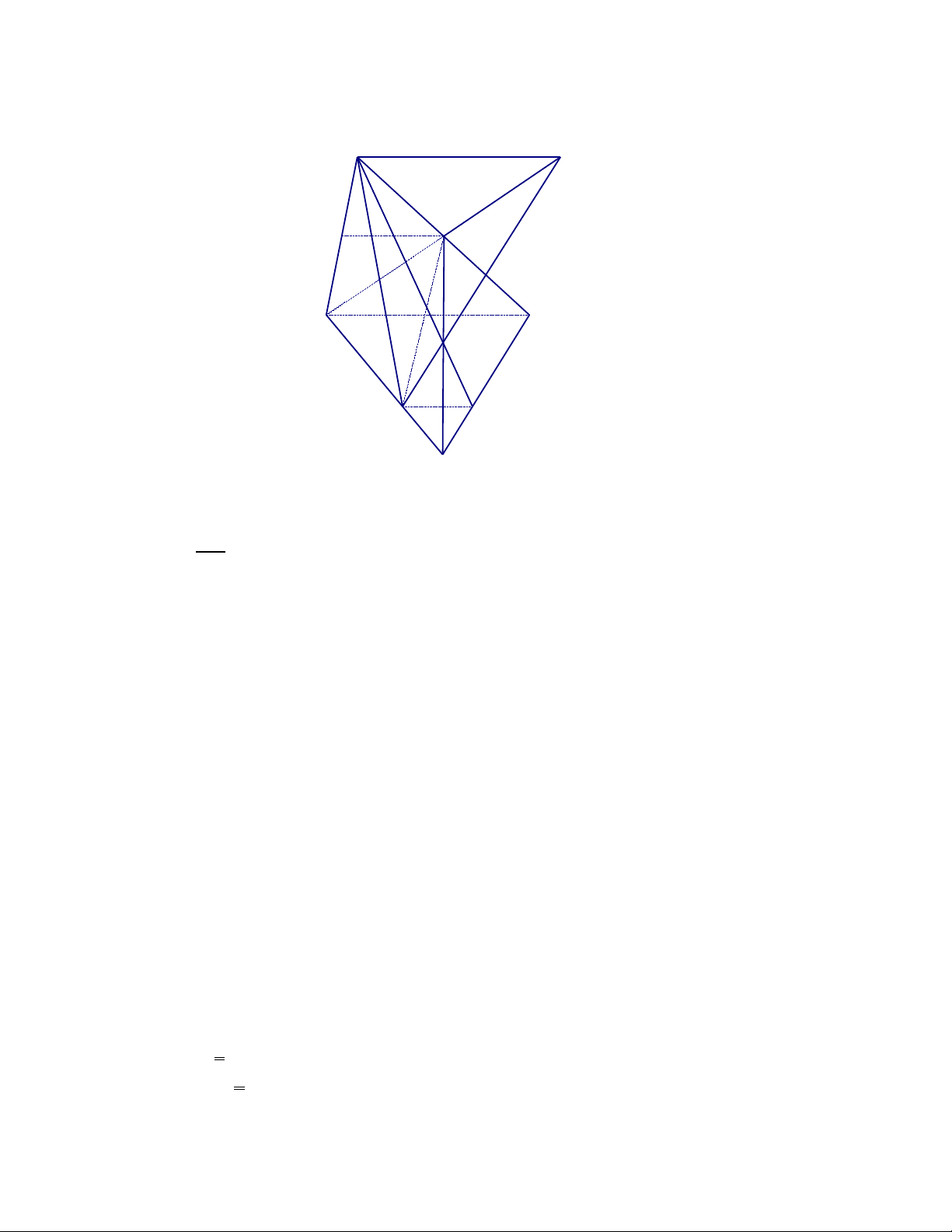
3. Cho t di n ABCD .G i I ,J l n l t là tr ng tâm các tam giác ABC và ABD.ứ ệ ọ ầ ượ ọ
Ch ng minh : IJ ứ⁄ ⁄ CD
Gi iả
G i E là trung đi m AB ọ ể
Ta có :
DEJ
CEI
IJ và CD đng ph ng ồ ẳ
Do đó :
3
1
ED
EJ
EC
EI
(tính ch t tr ng tâm)ấ ọ
V y : IJ // ậCD
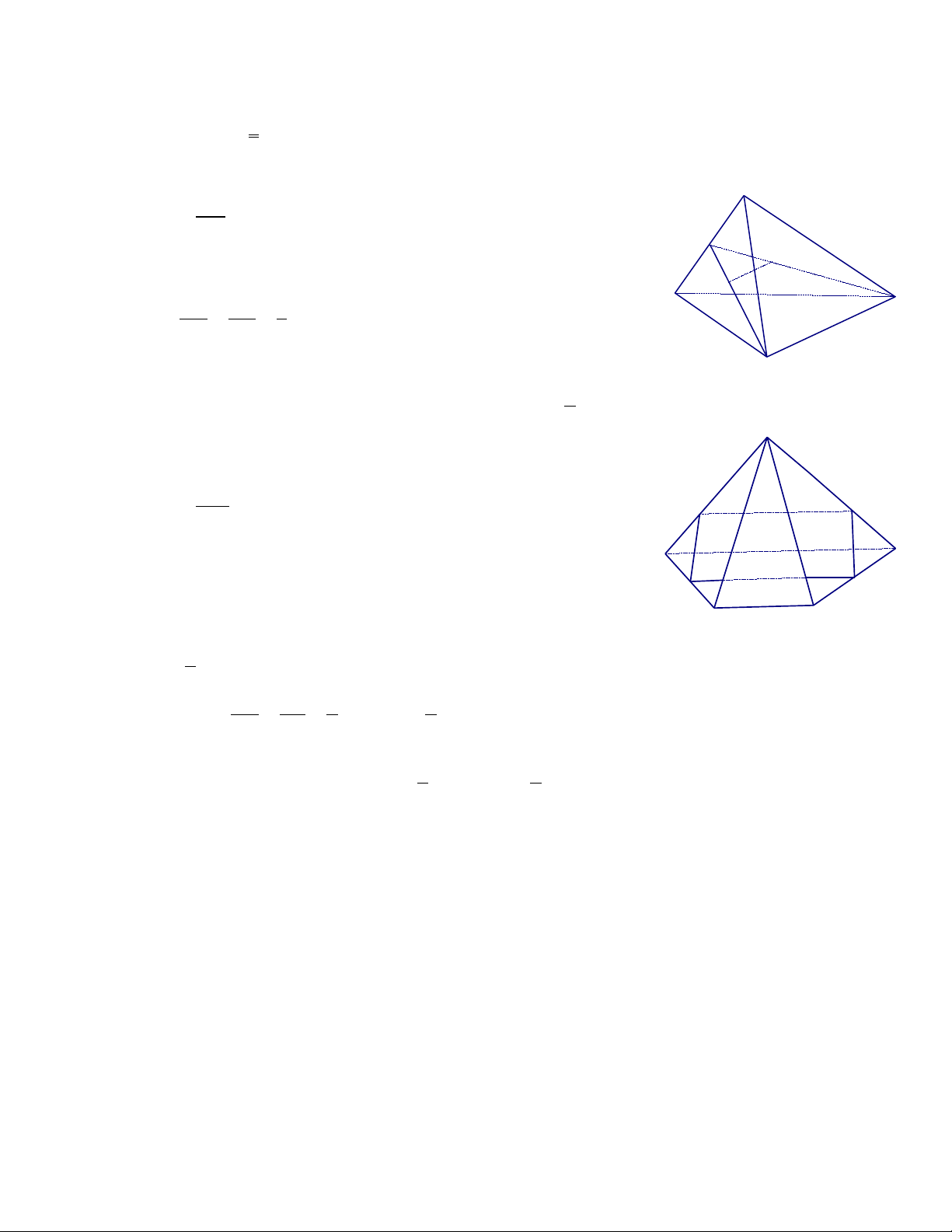
4. Cho hình chóp S.ABCD có đáy ABCD là hình thang (đáy l n AB). G i I, J l n l t là ớ ọ ầ ượ
trung đi m ểAD và BC , K là đi m trên c nh SB sao cho SN = ể ạ
3
2
SB .
a. Tìm giao tuy n c a (SAB) và (IJK)ế ủ
b. Tìm thi t di n c a (IJK) v i hình chóp S.ABCDế ệ ủ ớ
Tìm đi u ki n đ thi t di n là ề ệ ể ế ệ hình bình hành
Gi i ả
a. Tìm giao tuy n c a (SAB) và (IJK)ế ủ :
Ta có : AB ⁄ ⁄ IJ và K là đi m chung c a (SAB) và (IJK)ể ủ
V y : giao tuy n là đng th ng Kx ậ ế ườ ẳ song song AB
b. Tìm thi t di n c a (IJK) v i hình chóp S.ABCDế ệ ủ ớ :
G i L = ọKx SA
Thi t di n là hình thang IJKLế ệ
Do : IJ là đng trung bình c a hình thang ABCDườ ủ
IJ =
2
1
(AB + CD)
Xét SAB có :
3
2
SB
SK
AB
LK
LK =
AB.
3
2
IJKL là hình bình hành IJ = KL
2
1
(AB + CD) =
AB.
3
2
AB = 3.CD
V y : ậthi t di n IJKL là ế ệ hình bình hành AB = 3.CD
L
S
C
B
J
I
K
D
A
J
I
E
C
D
B
A