A
B
C
D
F
G
E
H
K
CẤU TRÚC DỮ LIỆU VÀ
GIẢI THUẬT (501040)
Chương 5: Đệ qui
ĐH Bách Khoa Tp.HCM Chương 5: Đệ qui 2
Khoa Công nghệ Thông tin
Khái niệm đệ qui
Khái niệm (định nghĩa) đệ qui có dùng lại chính
nó.
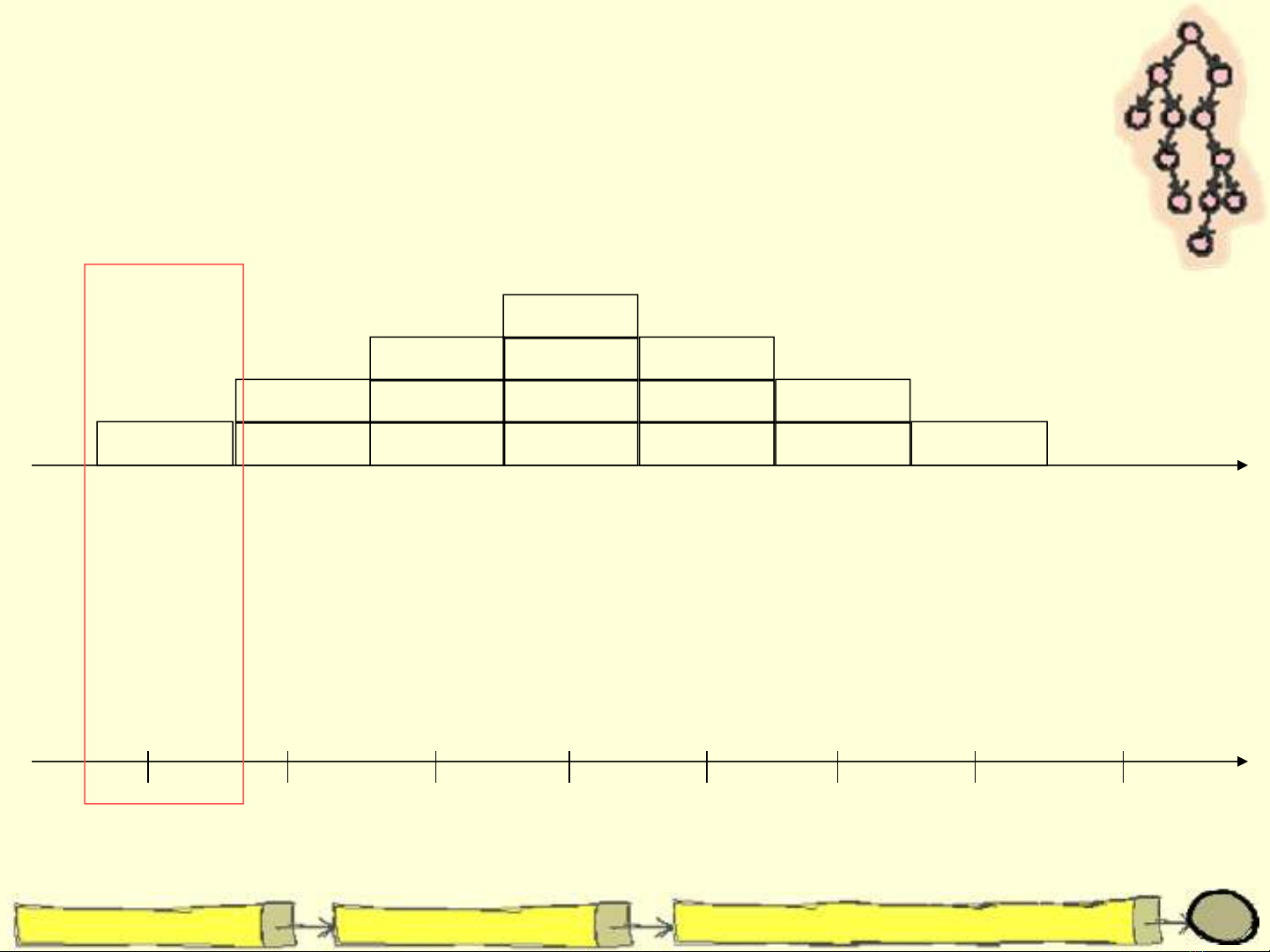
Ví dụ: giai thừa của n là 1 nếu n là 0 hoặc là n nhân
cho giai thừa của n-1 nếu n > 0
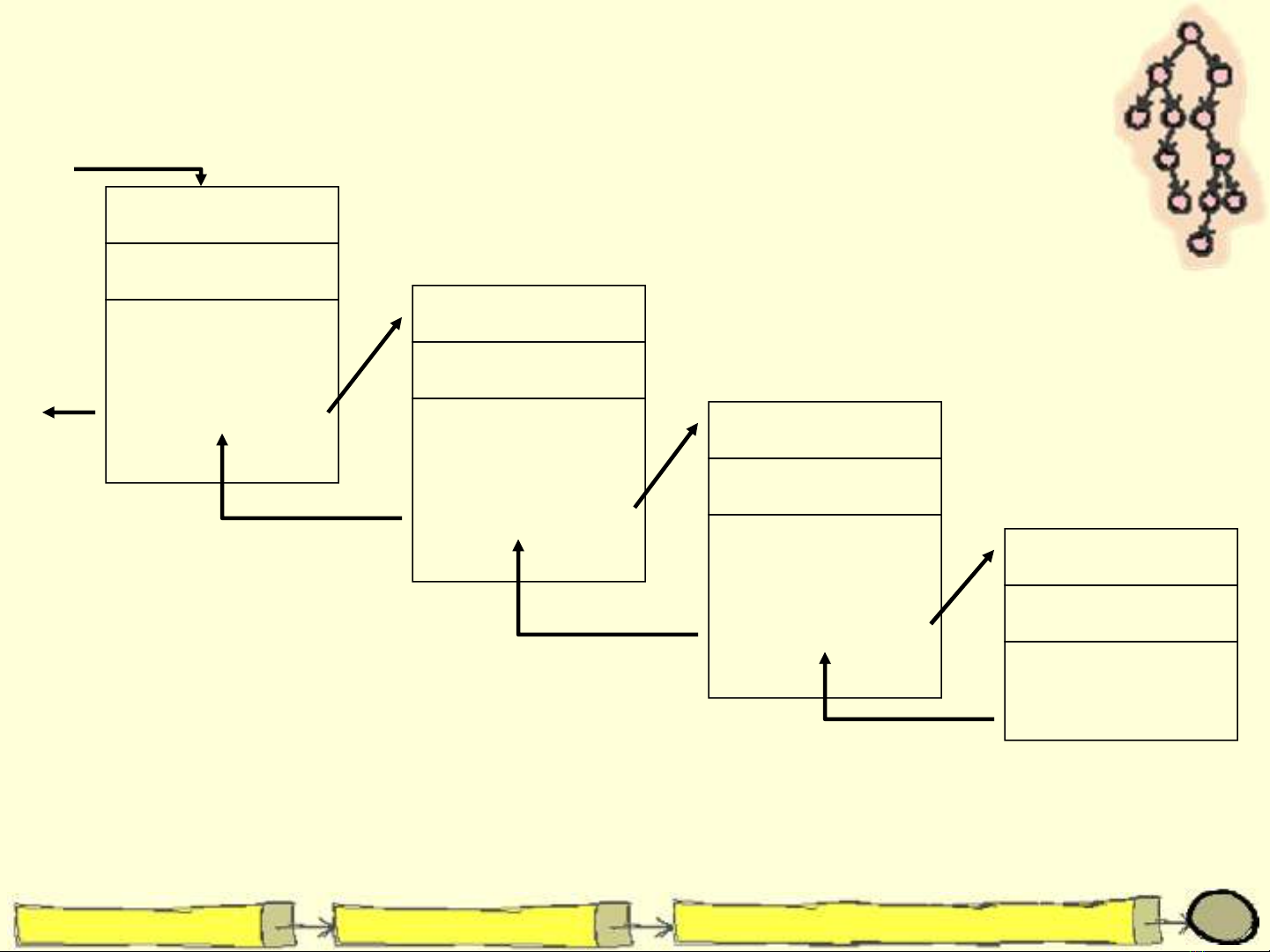
Quá trình đệ qui gồm 2 phần:
Trường hợp cơ sở (base case)
Trường hợp đệ qui: cố gắng tiến về trường hợp cơ
sở
Ví dụ trên:
Giai thừa của n là 1 nếu n là 0
Giai thừa của n là n * (giai thừa của n-1) nếu n>0
ĐH Bách Khoa Tp.HCM Chương 5: Đệ qui 3
Khoa Công nghệ Thông tin
Tính giai thừa
Định nghĩa không đệ qui:
n! = n * (n-1) * … * 1
Định nghĩa đệ qui:
n! = 1 nếu n=0
n * (n-1)! nếu n>0
Mã C++:
int factorial(int n) {
if (n==0) return 1;
else return (n * factorial(n - 1));
}
ĐH Bách Khoa Tp.HCM Chương 5: Đệ qui 4
Khoa Công nghệ Thông tin
Thi hành hàm tính giai thừa
n=2
…
2*factorial(1)
factorial (2)
n=1
…
1*factorial(0)
factorial (1)
n=0
…
return 1;
factorial (0)
1
1
6
2
n=3
…
3*factorial(2)
factorial (3)
ĐH Bách Khoa Tp.HCM Chương 5: Đệ qui 5
Khoa Công nghệ Thông tin
Trạng thái hệ thống khi thi hành hàm
tính giai thừa
factorial(3) factorial(3)
factorial(2)
factorial(3)
factorial(2)
factorial(1)
factorial(3)
factorial(2)
factorial(1)
factorial(0)
factorial(3)
factorial(2)
factorial(1)
factorial(3)
factorial(2)
factorial(3)
t
Gọi hàm
factorial(3)
Gọi hàm
factorial(2)
Gọi hàm
factorial(1)
Gọi hàm
factorial(0)
Trả về từ
hàm
factorial(0)
Trả về từ
hàm
factorial(1)
Trả về từ
hàm
factorial(2)
Trả về từ
hàm
factorial(3)
Stack hệ thống
Thời gian hệ thống
t