Bài giảng Điện tử học phần VKT xây dựng dân dụng - GV. Nguyễn Hoàng Giang

Chia sẻ: Minh Minh | Ngày: | Loại File: PDF | Số trang:126

Thêm vào BST

Báo xấu

184
lượt xem 40
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Điện tử học phần VKT xây dựng dân dụng của GV. Nguyễn Hoàng Giang gồm 2 phần, trình bày về hình họa phối cảnh, vẽ hình chiếu phối cảnh theo hai hình chiếu thẳng góc, vẽ xây dựng, bổ sung những khái niệm cơ bản trong xây dựng, bản vẽ kết cấu thép, bản vẽ kết cấu bê tông cốt thép, bản vẽ kết cấu gỗ và bản vẽ nhà.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Điện tử học phần VKT xây dựng dân dụng - GV. Nguyễn Hoàng Giang

TRƯỜNG CAO ĐẲNG KINH TẾ KỸ THUẬT KHOA: KỸ THUẬT CÔNG NGHIỆP BÀI GIẢNG ĐIỆN TỬ HỌC PHẦN VKT XÂY DỰNG DÂN DỤNG GV: NGUYỄN HOÀNG GIANG
PHẦN I: HÌNH HỌA PHỐI CẢNH CHƯƠNG I: MỞ ĐẦU 1.1. Khái niệm chung về hình chiếu phối cảnh Trong học phần Vẽ Kỹ thuật I đã trình bày phương pháp biểu diễn vật thể nhờ phép chiếu song song, phép chiếu vuông góc và phép chiếu xuyên tâm. Những hình biểu diễn vẽ theo phương pháp phép chiếu song song không cho ta ấn tượng giống như khi nhìn trực tiếp các đối tượng trong thực tế có kích thước lớn như là nội thất, những đối tượng nhà cửa, đê đập, cầu cống...
Vì vậy, trong xây dựng, kiến trúc, người ta dùng một loại hình biểu diễn xây dựng trên cơ sở của phép chiếu xuyên tâm, gọi là h/c phối cảnh (HCPC). Có nhiều loại HCPC. Có loại HCPC vẽ trên mặt trụ hay trên mặt cầu, gọi là HCPC trụ hay HCPC cầu, phối cảnh nhà hát, phối cảnh nổi (dùng trong nghệ thuật phù điêu) hay phối cảnh động ... Trong giáo trình này ta chỉ nghiên cứu loại HCPC vẽ trên mặt phẳng, gọi là hình chiếu phối cảnh phẳng.
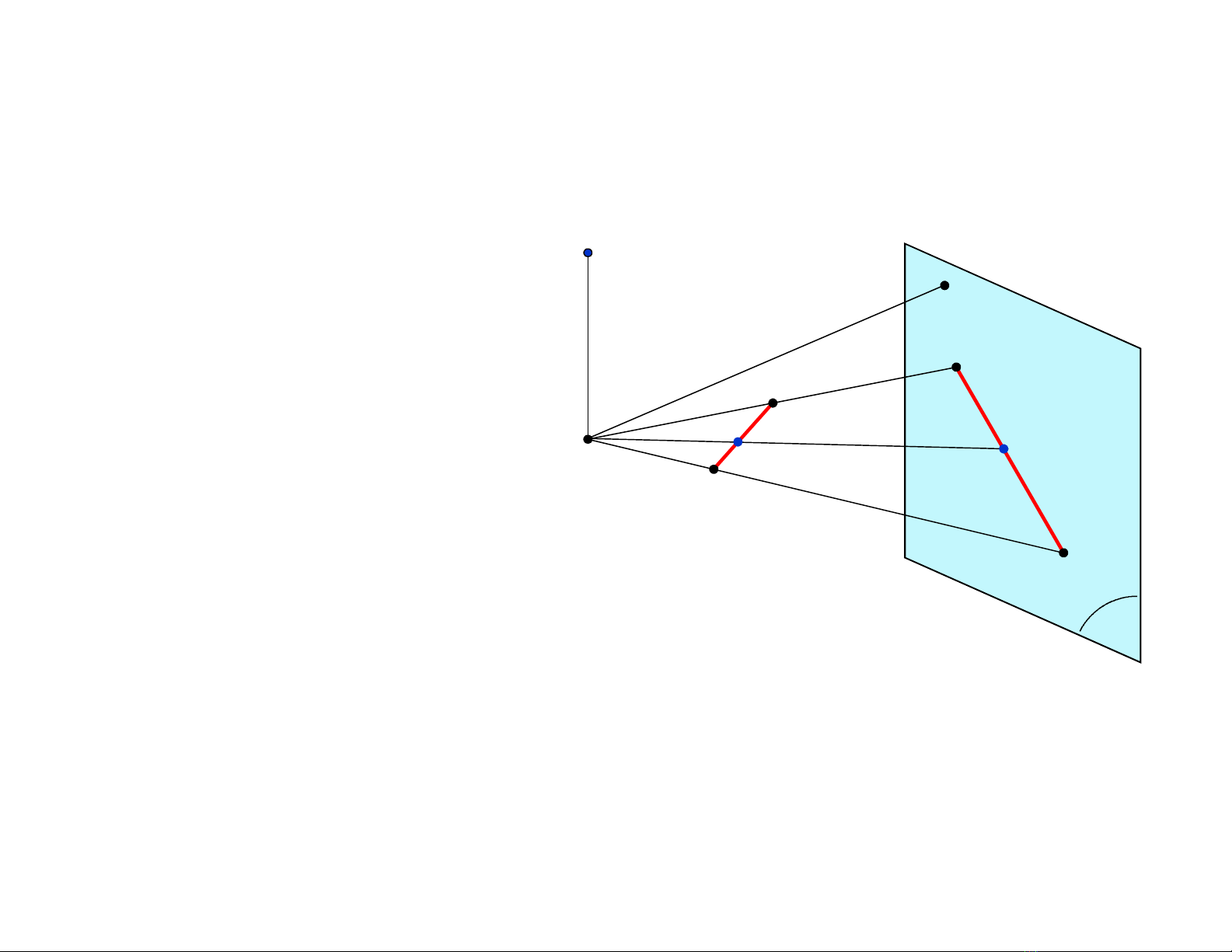
1.2. Phép chiếu xuyên tâm 1. Định nghĩa Trong không gian, lấy mp P làm mp hình chiếu và một điểm S ngoài P làm tâm chiếu. A’∞ M Hình chiếu xuyên tâm của điểm A ’ được xác định như sau: m A’ A - Nối SA, tìm giao điểm A’ của SA S C’ với mặt phẳng P B C - SA gọi là đường thẳng chiếu hoặc tia chiếu B’ - A’ là h/c xuyên tâm của điểm A 2. Tính chất P * Tính chất 1: H/c xuyên tâm của 1 đường thẳng (không đi qua tâm chiếu) là 1 đường thẳng - Hệ quả: + SA // P thì A’ ∞ + Nếu C  AB thì C’  A’B’ + Nếu đthẳng qua tâm chiếu S thì h/c xtâm suy biến thành 1 điểm
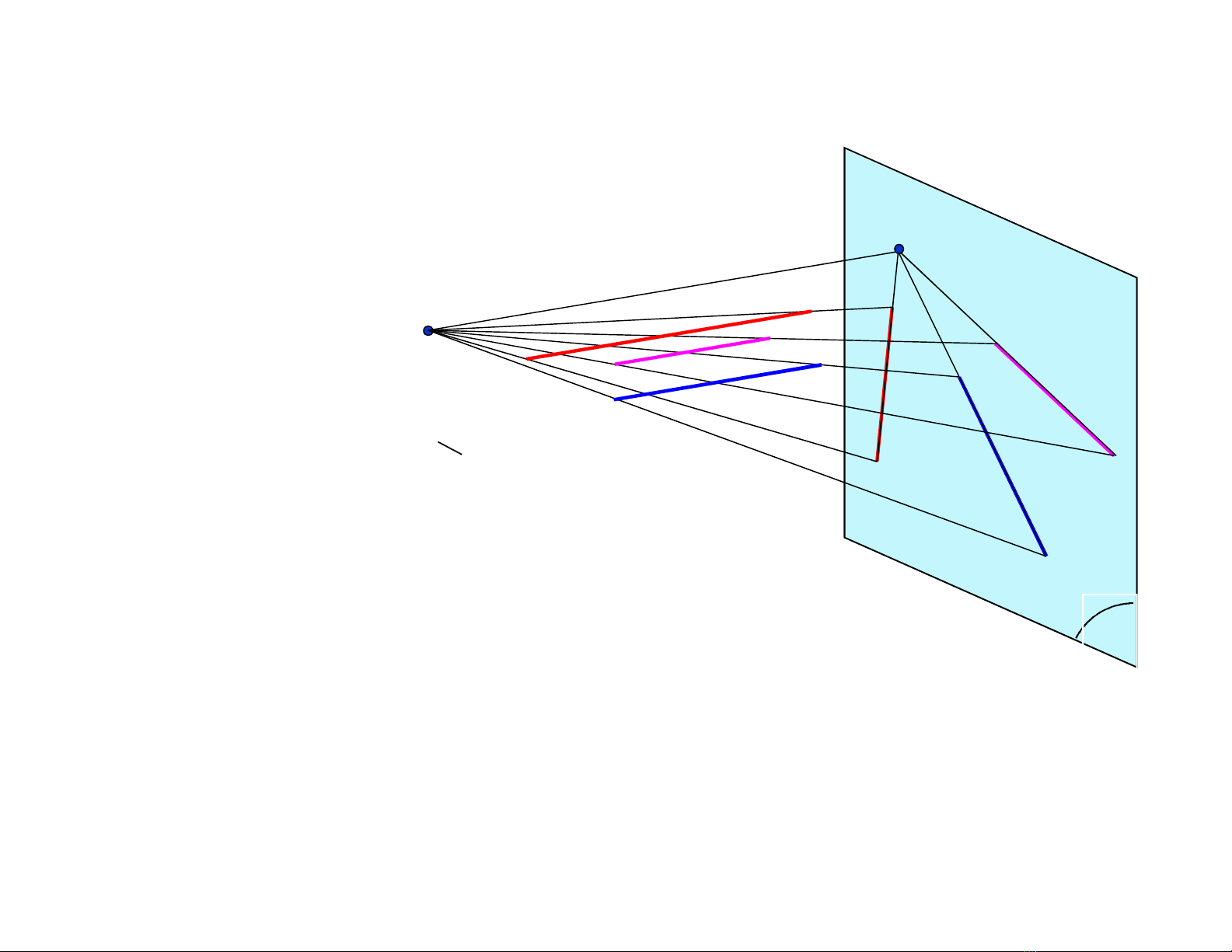
* Tính chất 2: H/c xuyên tâm của các đường thẳng song song là các đường thẳng đồng quy K’ k B’ B S D D’ A C F - Chứng minh t/c 2: F’ E Ta có: AB // CD // EF và // P A’ C’ Các h/c xuyên tâm của chúng là A’B’, C’D”, E’F’ sẽ đồng quy tại K’, vì: E’ + Các mp SAB, SCD, SEF có 1 điểm chung là S sẽ cắt nhau theo giao tuyến k đi qua S và k // AB, CD và EF P + Đường thẳng k cũng là giao tuyến của các mp SA’B’, SC’D’ và SE’F’ + Giao tuyến k cắt P tại điểm K’ + K’ là điểm chung của A’B’, C’D’ và E’F’ là các h/c xtâm của các mp SAB, SCD và SEF
CHƯƠNG II: ĐIỂM, ĐƯỜNG THẲNG, MẶT PHẲNG 2.1. Hệ thống phối cảnh * Hệ thống phối cảnh phẳng gồm các yếu tố sau: - Mặt tranh T : Mp thẳng đứng, T trên đó sẽ vẽ HCPC  t M’ - Mặt phẳng vật thể V : Mp nằm k t ngang, trên đó sẽ đặt các đối tượng M cần biểu diễn (V T) đ - Điểm nhìn M: Điểm ứng với vị V trí mắt của người quan sát (là tâm M2 đ chiếu) * Các tên gọi trong hệ thống phối cảnh: - Hình chiếu vuông góc M’ của M trên T gọi là điểm chính của tranh - Hình chiếu vuông góc M2 của M trên V gọi là điểm đứng hay điểm chân - Tia MM’ gọi là tia chính ; khoảng cách k = MM’ gọi là khoảng cách chính - Giao tuyến đđ của T với V gọi là đáy tranh - Giao tuyến tt của T với mp bằng đi qua M gọi là đường chân trời.
- Mặt phẳng  đi qua M và song song với T chia không gian thành 2 phần: + Phần không gian chứa mặt tranh gọi là không gian thấy + Phần không gian còn lại gọi là không gian khuất Mặt phẳng  gọi là mp trung gian A 2.2. Phối cảnh của điểm T 1. Cách xây dựng và các định nghĩa A’ t * Giả sử có điểm A bất kỳ trong M’ kgian. Ta xây dựng phối cảnh của A như sau: M t A2’ - Chiếu thẳng góc điểm A lên V đ M2’ A2 (từ tâm chiếu S∞ của đường thẳng V M2 đ với V ) được điểm A2 - Chiếu xuyên tâm A và A2 từ tâm M lên T, ta được A’ và A2’ Vì mp MAA2 V nên A’A2’ đđ Vậy, phối cảnh của điểm A được biểu diễn bằng cặp điểm A’, A’2 với A’A’2 đđ.
A’ * Phối cảnh của điểm A được biểu diễn như hình bên. Trong đó: t t - A’ gọi là hình chiếu chính của A (còn được gọi là phối cảnh của A) A’2 - A’2 gọi là hình chiếu thứ hai của A. đ đ - Đường thẳng A’A’2 gọi là đường dóng. 2. Phối cảnh của 1 số điểm đặc biệt - Nếu B  mặt tranh T thì B’  B và T B’2  B2  đđ B’ B B’ M t t đ B’2  B2 M’2 đ đ đ V B’2  B2
- Nếu C  mp vật thể V thì C2  C và C’2 C’ T t t M C’2C’ C’2  C’ 2 đ đ C2  C - Nếu D∞ là điểm vô tận của mp V M’2 V ( MD∞ // V ) thì D’2  D’  tt T t M D’  D’2 D’2  D’ t t D∞ đ t V đ đ D∞ M’2 đ
- Nếu E là điểm của mp trung gian  ( E  ), ( ME // T , ME2 // T ) thì E’,E’2 là những điểm vô tận của T  T E’∞ E’ E M t t đ E2 E’2 M2 đ E’2∞ đ đ V - Nếu F là điểm vô tận của không T F’ gian thì F2 là điểm vô tận của mp V t F∞ F∞ F’2 tt F’ M F’2 t t t đ V F’2 M’ F2∞ 2 đ đ đ
* Những điểm đặc biệt của không gian: Z∞ T - Gọi Z∞ là điểm vô tận của hướng t Z∞ chiếu vuông góc với mp V. M’ M - Đường thẳng M Z∞ được gọi là t đường tâm chiếu. đ V - Những điểm thuộc đường tâm chiếu M2 M’2 đ được gọi là những điểm đặc biệt của không gian. Những điểm này sẽ có h/c chính và h/c thứ hai trùng nhau tại điểm vô tận của đường dóng. - Những điểm đặc biệt ( trừ hai tâm chiếu M và Z∞ ) sẽ được biểu diễn bằng cách gắn chúng lên một đường thẳng đặc biệt.
2.3. Phối cảnh của đường thẳng Phối cảnh của đg thẳng được xác định bởi p/cảnh của 2 điểm  đg thẳng 1. Phối cảnh của đường thẳng bất kỳ B’ Đg thẳng bất kỳ thì p/cảnh của nó có vị trí bất d’ kỳ trên đồ thức t t Đg thẳng bất kỳ d (AB) có h/c chính là d’ và A’ h/c thứ hai là d’2 B’ 2. Phối cảnh của đường thẳng đặc biệt d’2 2 A’ Là đường thẳng có hai h/c trùng nhau trên đ đ 2 một đường dóng. M’ Điều kiện cần và đủ để hai t N’ t h/chiếu của một đường thẳng trùng nhau trên một đường N’2 dóng là đường thẳng đó phải cắt đường tâm chiếu (không đi đ M’ đ 2 qua M)
a- Đường thẳng chiếu phối cảnh: Là đường thẳng đi qua tâm chiếu M  C’ D’ ; C’2D’2 đđ D C’ D’ T C C’ D’ M t t D’2 D’2 đ C’2 D2 C2 C’2 M’2 đ đ đ V
b- Đường thẳng chiếu bằng: Là đường thẳng đi qua tâm chiếu Z∞  E’2 F’2 ; E’F’ đđ Z∞ T E’ E E’ M t t F’ F’ đ F E’2 F’2 đ E’2  F’2 đ M’2 đ E2  F 2 V
d’ 3- Sự liên thuộc của điểm và đường thẳng A’ a- Điểm thuộc đường thẳng bất kỳ t t Điều kiện cần và đủ để 1 điểm thuộc 1 đường thẳng bất kỳ là: d’2 - H/c chính của điểm h/c chính của đthg A’2 - H/c thứ 2 của điểm h/c thứ 2 của đthg đ đ Ad A’  d’ A’ A’2  d’2 C’ b- Điểm thuộc đường thẳng đặc biệt Nếu đường thẳng là đặc biệt thì điều kiện B’ t t trên chưa đủ. C A’2 C  AB  có thêm điều kiện: B C’2 (A’,B’,C’) = (A’2,B’2,C’2) đ B’2 đ
4- Điểm tụ và vết của đường thẳng d’ t E’ t a- Điểm tụ của đường thẳng 2 * Điểm tụ của đthg (E): Là p/cảnh của điểm vô tận của đthg  E’2 = d’2 tt d’2 E’ đ đ * Các đường thẳng song song nhau sẽ có E’ chung điểm tụ d’ Nếu d // k sẽ có chung điểm tụ E k’ t E’2 t d’2 k’2 = E’2  tt  d’ k’ = E’ d’2 k’2 đ đ
* Biểu diễn điểm tụ của một số đường thẳng N’∞ d’ b’ h’ n’ D’  M’ t t D’2 H’  H’2 N’2∞ b’2 k n’2 d’2 h’2 đ đ - Đường thẳng d // V . Điểm tụ của d là D’ tt, do đó D’  D’2 - Đường thẳng b T . Điểm tụ của b là điểm chính M’ - Đường thẳng n // T . Điểm tụ của n là điểm vô tận N’∞ của n - Đường thẳng h hợp với T một góc 450. Điểm tụ của H’ của h đứng cách điểm chính M’ một khoảng bằng khoảng cách chính k. ( M’H’ = k )
b- Vết của đường thẳng * Vết bằng của đường thẳng (V): Là giao điểm của đường thẳng với mp vật thể V  (V’2  V’) * Vết tranh của đg thẳng (T): Là giao điểm của đường thẳng với mp tranh T  T’2 = d’2 đđ T’ d’ d’ t t t t V’2  V’ d’2 d’2 đ đ đ đ T’2
5- Vị trí tương đối của hai đường thẳng a- Hai đường thẳng cắt nhau * Cả hai đường thẳng đều là bất kỳ: a’ b’ = K’ Điều kiện: các h/c chính cắt nhau, các a’2 b’2 = K’2 a b=K h/c thứ 2 cắt nhau và các giao điểm K’ K’2 đđ cùng nằm trên 1 đường dóng. a’ K’ b’ K’∞ b’ a’ t t t t K’2∞ K’2 b’2 a’2 b’2 đ đ a’2 đ đ Trường hợp a b = K  mp trung gian 
A’ * Trường hợp một đường thẳng là đặc biệt: d AB = K K’ d’ a’ b’ = K’ Các điều kiện: B’ t t a’2 b’2 = K’2 Ngoài các điều kiện nếu trên, phải có d’2 B’2 thêm điều kiện. K’2 (A’,B’,K’) = đ A’2 đ (A’2,B’2,K’2) * Trường hợp cả hai đường thẳng là đặc biệt:  AB vµ CD t¹o thµnh 1 mp, trong mp nµy, c¸c ®êng th¼ng AC vµ BD hoÆc AD vµ BC sÏ c¾t nhau hoÆc // nhau