L P TRÌNH JAVA C B NẬ Ơ Ả
L P TRÌNH JAVA C B NẬ Ơ Ả
Ch ng 4ươ
CÁC KI U S Ể Ố
VÀ BI U TH CỂ Ứ
Lê Tân
B môn: L p trình máy tínhộ ậ
2/23
N i dung ch ng 4ộ ươ
T ng quan v các ki u d li u Java ổ ề ể ữ ệ
Các ki u d li u s ể ữ ệ ố
Khai báo các ki u s ể ố
Các bi u th c s h c đ n gi n ể ứ ố ọ ơ ả
Chuy n đ i ki u (ép ki u) ể ổ ể ể
Các ph ng th c c a l p Math (toán h c) ươ ứ ủ ớ ọ
Các ph ng th c c a l p String (chu i) ươ ứ ủ ớ ỗ
3/23
4.1 T ng quan v ổ ề
4.1 T ng quan v ổ ề các ki u d li u Javaể ữ ệ
các ki u d li u Javaể ữ ệ
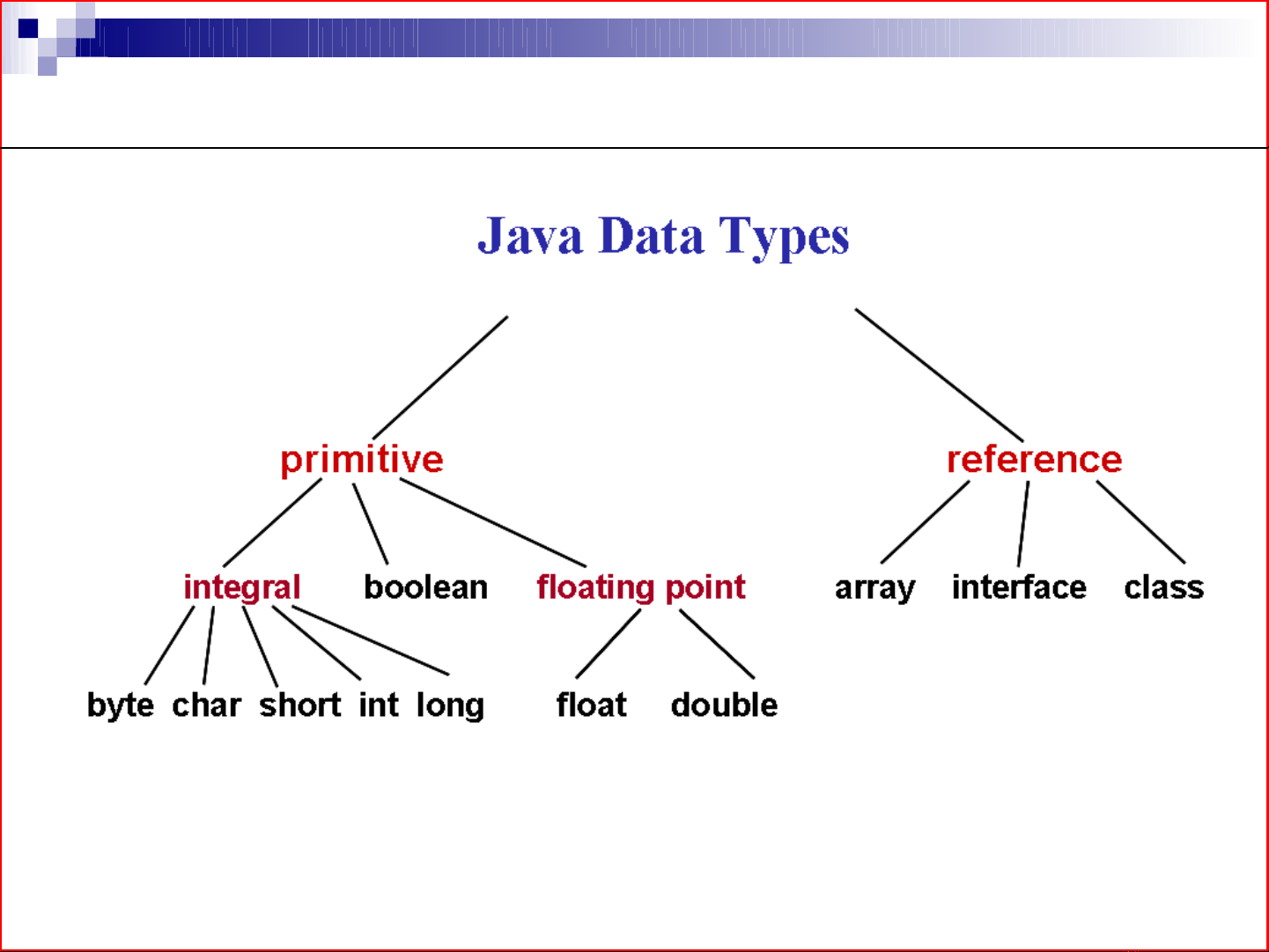
Các ki u d li u Java:ể ữ ệ Có hai d ng là d ng ạ ạ
nguyên thu và d ng tham chi u.ỷ ạ ế
•D ng nguyên thu : G m các ki u s nguyên, ạ ỷ ồ ể ố
ki u ểBoolean, và ki u s th c.ể ố ự
•D ng tham chi u: Ch a s các ph n t khác ạ ế ứ ố ầ ử
nhau, th ng là quá l n đ có th ch a v a ườ ớ ể ể ứ ừ
trong m t v trí nh đ n.ộ ị ớ ơ
Java l u đ i t ng đó vào m t ho c vài v trí ư ố ượ ộ ặ ị
trong ph n khác c a b nhầ ủ ộ ớ
V trí đã ch n cho bi n tham chi u s l u đ a ị ọ ế ế ẽ ư ị
ch mà đó đ i t ng có th đ c tìm th y. ỉ ở ố ượ ể ượ ấ
4/23
4.1 T ng quan v ổ ề
4.1 T ng quan v ổ ề các ki u d li u Javaể ữ ệ
các ki u d li u Javaể ữ ệ
5/23
Ki u s nguyên (integral number)ể ố
•Ki u s nguyên có th bi u di n các s nguyên ể ố ể ể ễ ố
khi khai báo v i t khoá ớ ừ byte, short, int, ho c ặ
long;
•Cũng có th bi u di n các ký t đ n khi khai ể ể ễ ự ơ
báo v i t khoá ớ ừ char.
•Các ki u s nguyên có đ dài nh sau:ể ố ộ ư
byte có đ dàiộ8 bits
short có đ dàiộ16 bits
int có đ dàiộ32 bits
long có đ dàiộ64 bits
4.2 C
4.2 Các ki u d li u sể ữ ệ ố
ác ki u d li u sể ữ ệ ố