
LÝ THUYẾT NHẬN DẠNG
CHƯƠNG 4:
PHÂN LỚP DỰA TRÊN TỐI ƯU
HÓA HÀM LƯỢNG GIÁ
Biên soạn: TS Ngô Hữu Phúc
Bộ môn: Khoa học máy tính
Học viện kỹ thuật quân sự
Email: ngohuuphuc76@gmail.com
Tối ưu hóa hàm lượng giá
1

4.1. GIỚI THIỆU CHUNG
Trong chương này tập trung vào việc thiết kế hàm phân biệt/mặt
quyết định có khả năng phân lớp theo một tiêu chí nào đó.
Với các kỹ thuật sử dụng bộ phân lớp Bayesian dựa trên ước
lượng hàm phân bố dữ liệu của mỗi lớp. Tuy nhiên, đây là nhóm
công việc phức tạp đối với dữ liệu có số chiều lớp.
Chương này đưa ra giải pháp xây dựng mặt quyết định mà
không cần sử dụng hàm phân bố của dữ liệu.
Giải pháp thuộc nhóm này đơn giản hơn so với phương pháp
phân lớp Bayesian, ngay cả đối với dữ liệu không nhiều.
2
Tối ưu hóa hàm lượng giá

4.1. GIỚI THIỆU CHUNG (CONT)
Để minh họa, thiết kế bộ phân lớp tuyến tính được mô tả:
𝑤𝑇𝑥 +𝑤0= 0
hay có thể viết lại:
𝑤′𝑇𝑥′ ≡ 𝑤𝑇,𝑤0𝑥
1
Như vậy, nếu 𝑤′ được ước lượng, một bộ dữ liệu xsẽ thuộc lớp
𝜔1𝜔2nếu:
𝑤′𝑇𝑥′= 𝑤𝑇𝑥 +𝑤0>< 0
Lưu ý: để đơn giản cách viết, có thể lược bỏ ký hiệu chuyển vị.
3
Tối ưu hóa hàm lượng giá
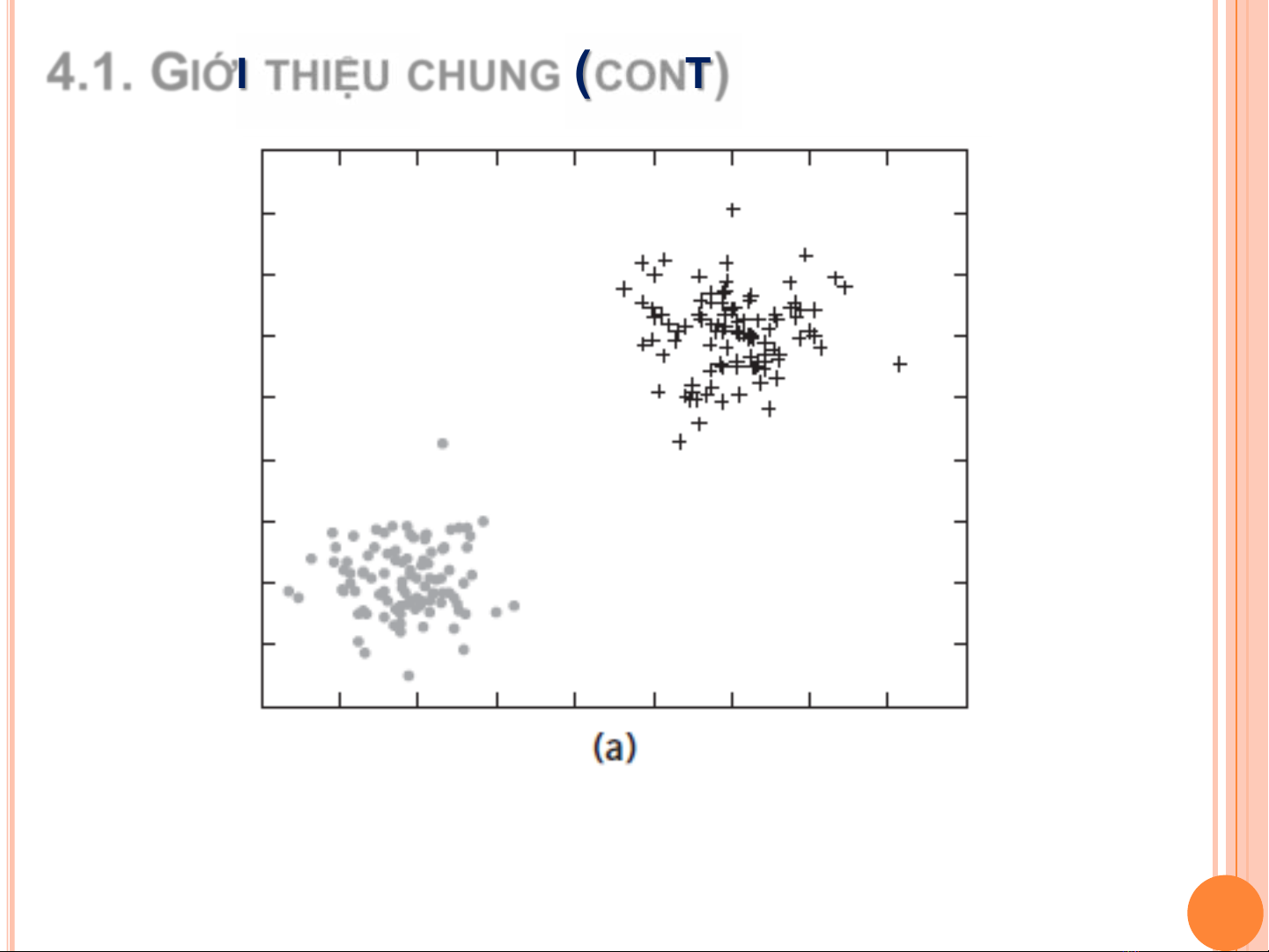
4.1. GIỚI THIỆU CHUNG (CONT)
Với dữ liệu trên, có thể dùng bộ phân lớp tuyến tính
4
Tối ưu hóa hàm lượng giá
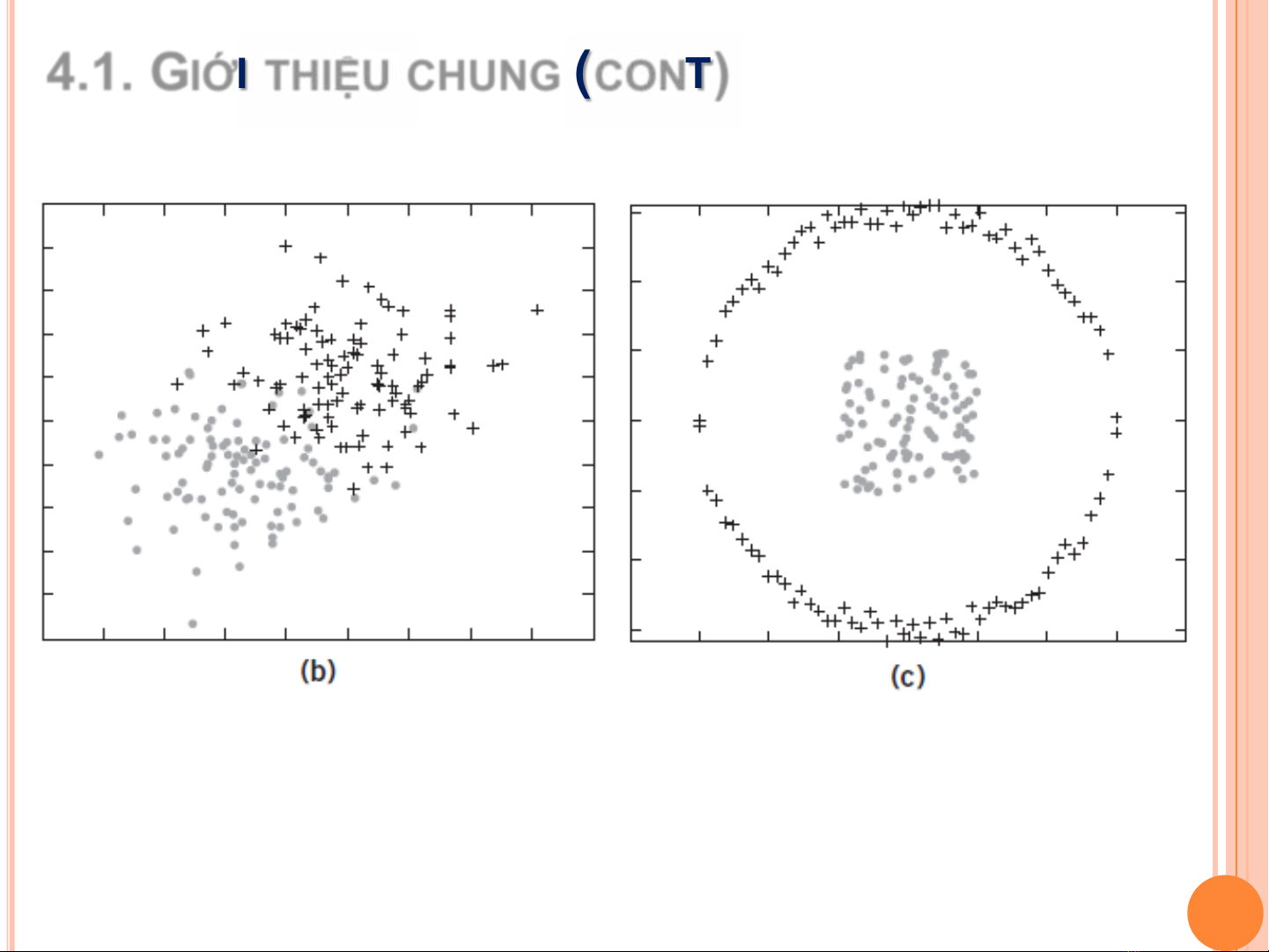
4.1. GIỚI THIỆU CHUNG (CONT)
Với dữ liệu trên, có thể dùng bộ phân lớp tuyến tính???
5
Tối ưu hóa hàm lượng giá


























