
Cây tìm kim nhphân (TKNP)
Dng cây TKNP
Cây TKNP cân bng
Cây -en
Cây AVL
Cây Treap
!a
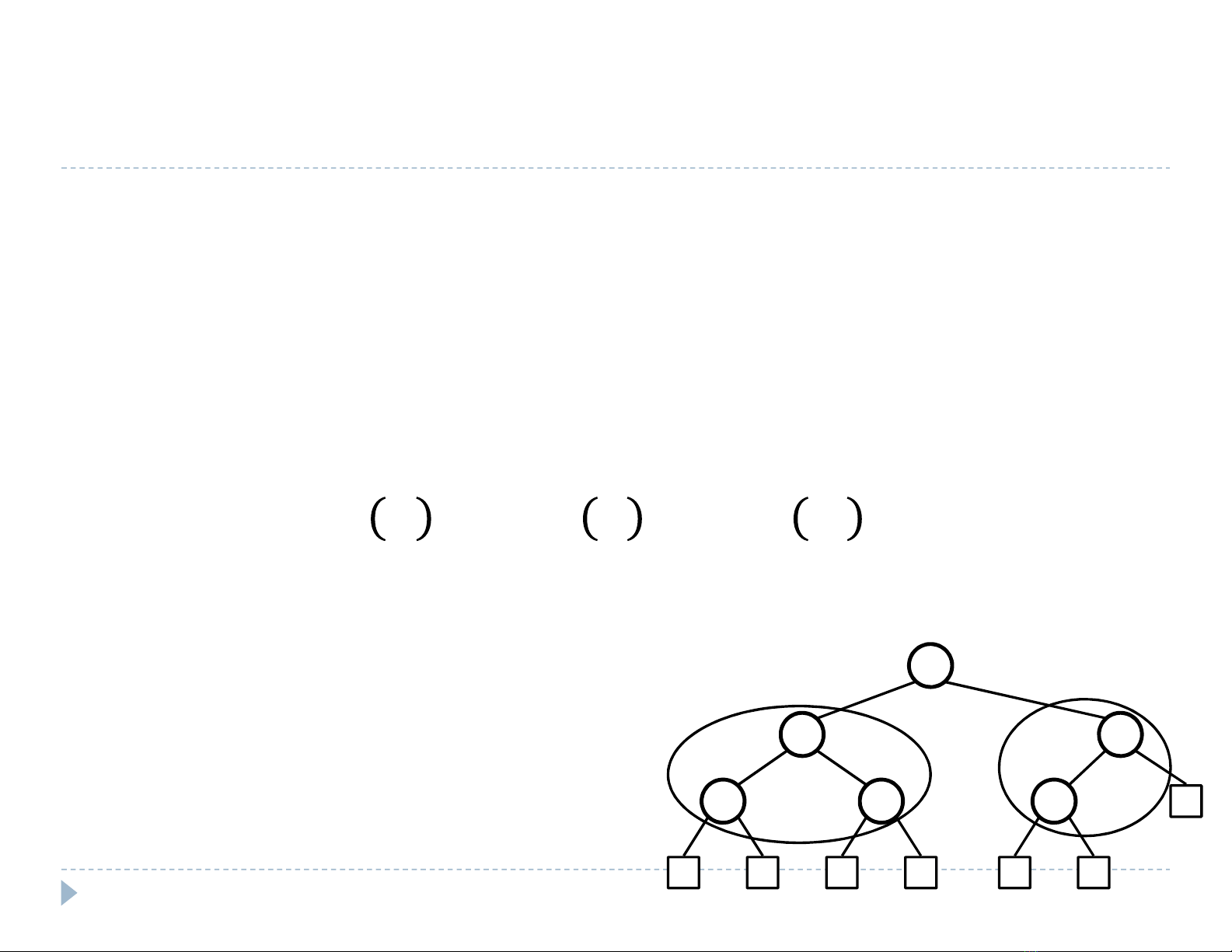
Cây TKNP:
cây nh phân
lưu khóa nh trong
lá rng
tha mãn tính cht:
≤ ≤
trong cây con trái ca
trong cây con phi ca
6
9
2
41 8

a #
Cây TKNP thc hin các tao thác chính
Truy vn: không thay i cu trúc cây TKNP
Tìm kim(SEARCH)
Nhnht (MINIMUM)
Ln nht (MAXIMUM)
Trưc (PREDECESSOR)
Sau (SUCCESSOR)
Sai: thay i cu trúc cây TKNP
Chèn (INSERT)
Xóa (DELETE)
#
trong cây con trái ca , trong cây con phi ca
≤ ≤
Duyt cây TKNP theo thttrong, thm các khóa theo
thttng dn
Sdng cây TKNP cho
cài t t in
Cây thtbphn (heap)
là cây tìm kim
là cây nhphân
không phi cây TKNP
dùng qun lý hàng iưu tiên


























