
nh ngha
Biu din
Tìm kim
Sp xp topo
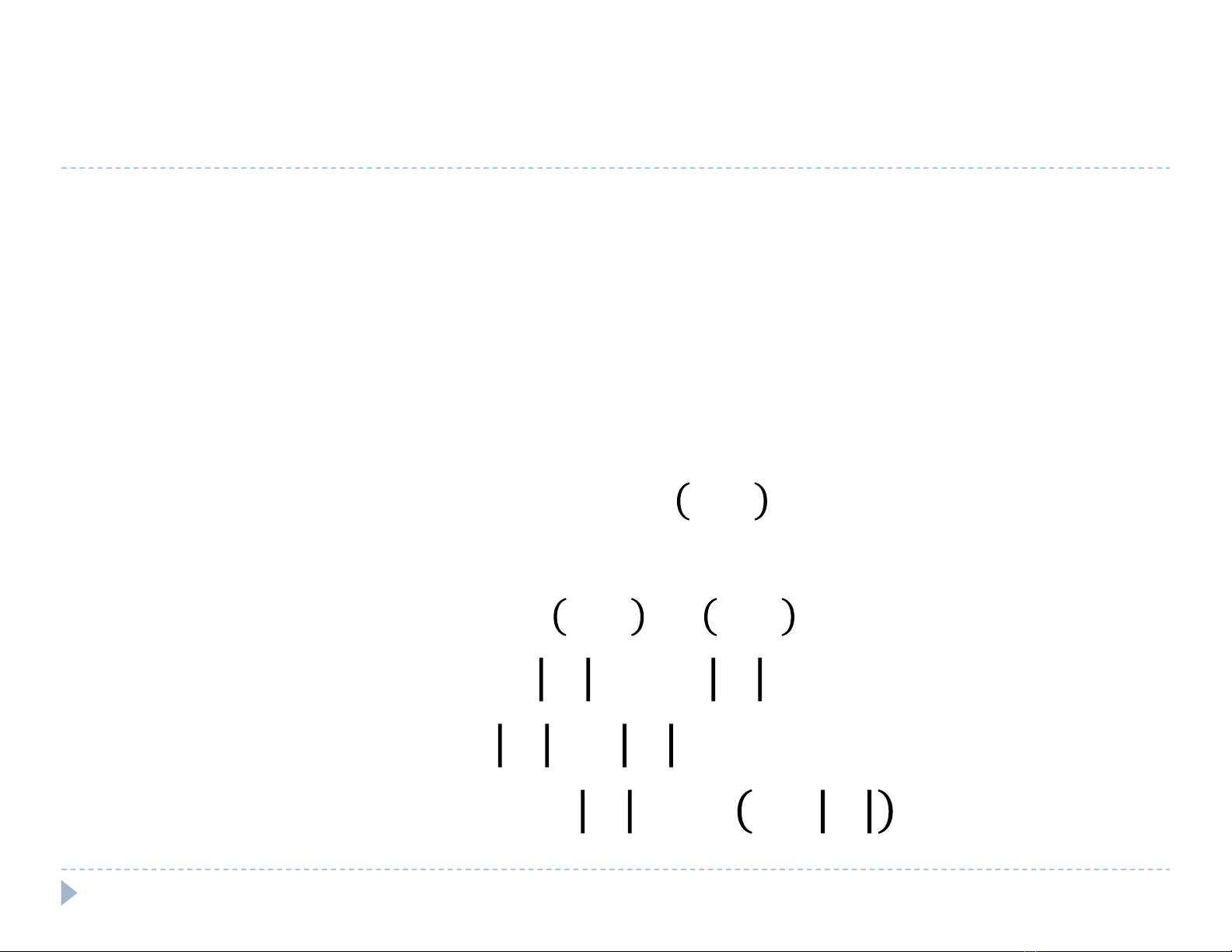
a
th = (, ) bao gm
Tp các nh
Tp ⊆ × cnh
thvô hng
Cp cnh không có tht, = (, )
th nh hng
Cp cnh có tht, ≠ ,
Chai trng hp, ∈ ( )
Nuliên thông, ≥ − 1
⟹
log
=
log

Danh sách lin k
Mng 1 chiudanh sách
Mi danh sách cho mtnh bao gm
Các nh sao cho , ∈
Ma trn lin k
Mng 2 chiu ×
nh cánh s1, 2, … ,
Giá tr1thhin có cnh , ∈
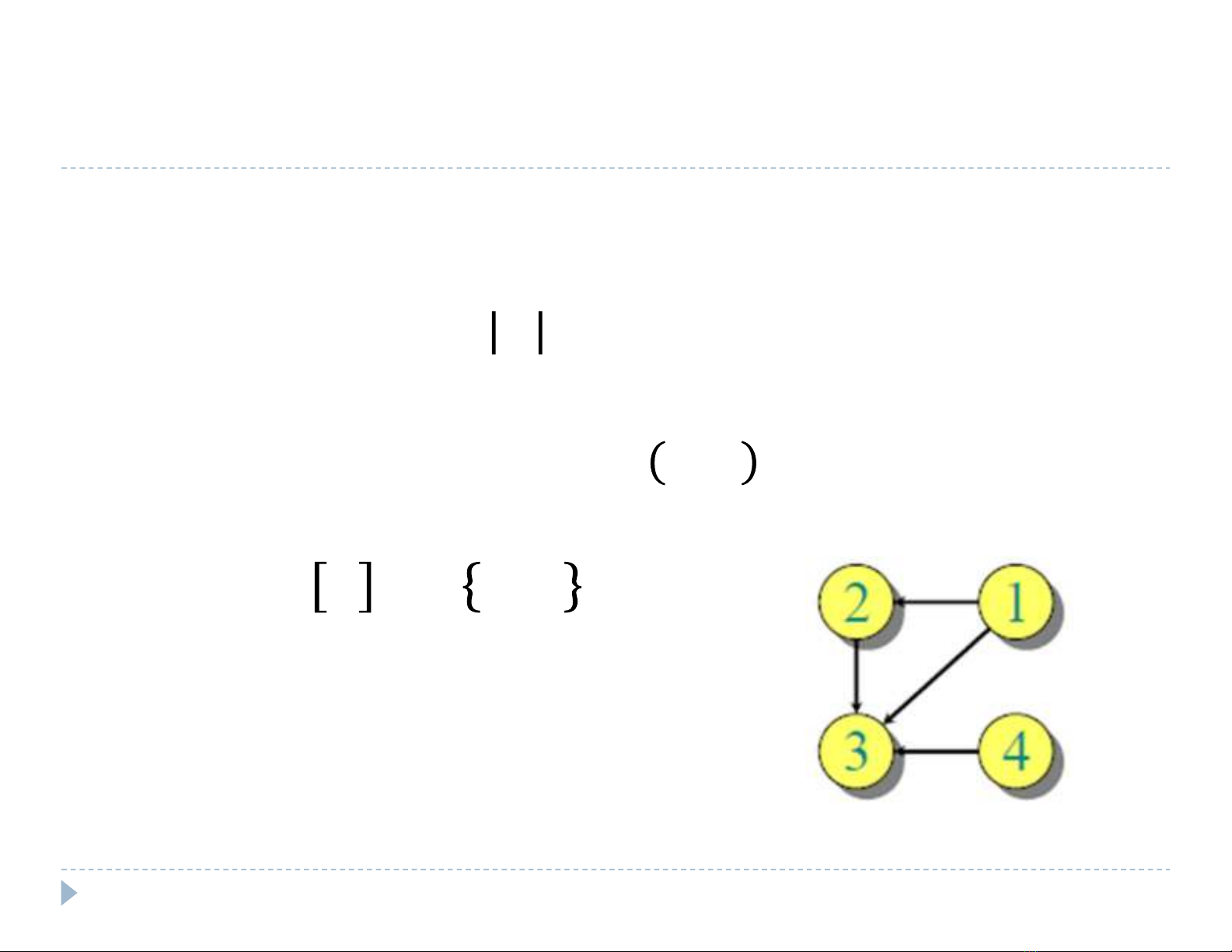
a
Danh sách lin k
Mng 1 chiudanh sách
Mi danh sách cho mtnh bao gm
Các nh sao cho
! "#
! "#
$! "#


























