Bài giảng Thống kê kinh doanh và SPSS - Bài 4: Kiểm định thống kê

Chia sẻ: Nguyễn Thị Hiền Phúc | Ngày: | Loại File: PPT | Số trang:44

Thêm vào BST

Báo xấu

140
lượt xem 22
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng cung cấp cho người học các kiến thức: Kiểm định thống kê. Hi vọng đây sẽ là một tài liệu hữu ích dành cho các bạn sinh viên đang theo học môn dùng làm tài liệu học tập và nghiên cứu.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Thống kê kinh doanh và SPSS - Bài 4: Kiểm định thống kê

Bài 4 KIỂM ĐỊNH THỐNG KÊ 1. Kiểm định trung bình 2. Kiểm định phi tham số 3. Kiểm định Khi bình phương Download trọn bộ IBM SPSS v19+crack và ebooks – articles tại http://www.mediafire.com/?1j5bcyb3asc8n
1.1. Kiểm định tmột mẫu Phương pháp kiểm nghiệp một mẫu được dùng để kiểm định có hay không sự khác biệt của giá trị trung bình của một biến đơn với một giá trị cụ thể, với giả thuyết ban đầu cho rằng giá trị trung bình cần kiểm nghiệm thì bằng với một con số cụ thể nào đó. Phương pháp kiểm nghiệm này dùng cho biến dạng thang đo khoảng cách hay tỉ lệ. Ta sẽ loại bỏ giả thuyết ban đầu khi kiểm nghiệm chó ta chỉ số Sig. nhỏ hơn mức tinh cậy (0.05). Download trọn bộ IBM SPSS v19+crack và ebooks – articles tại http://www.mediafire.com/?1j5bcyb3asc8n
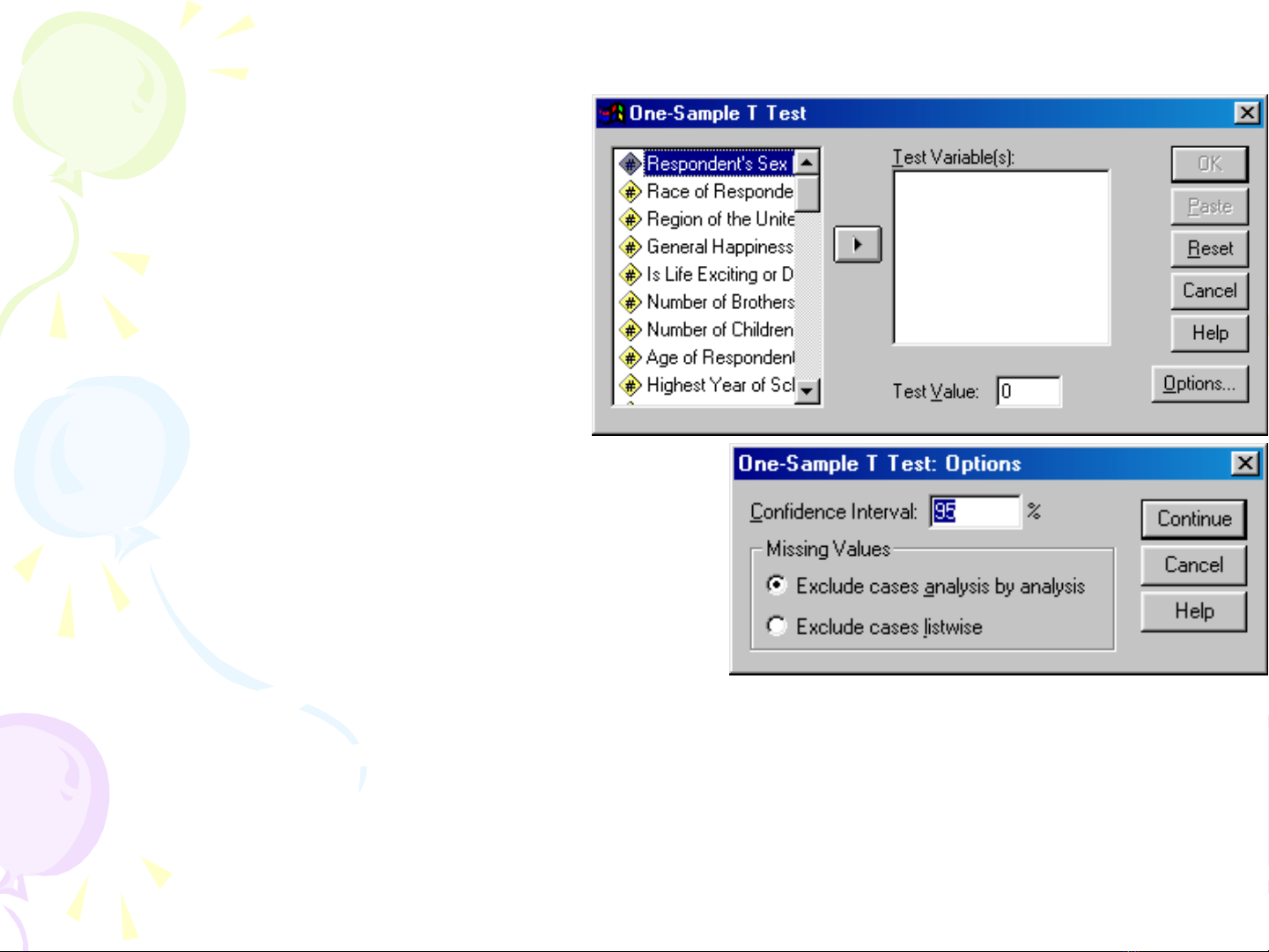
Compare Mean\OneSample T Test… Lựa chọn biến cần so sánh bằng cách di chuyển vệt đen và chuyển đến vào hộp thoại Test Variable(s), nhập giá trị cần so sánh vào hộp thoại Test Value Options để xác định độ tin cậy cho kiểm nghiệm, mặc định là 95% và cách xữ lý đối với các giá trị khuyết Exclude cases analysis by analysis. Mỗi kiểm nghiệm T sử dụng toàn bộ các trường hợp (cases) chứa đựng giá trị có ý nghĩa đối với biến được kiểm nghiệm. Đặc điểm là kích thước mẫu luôn thay đổi. Exclude cases listwise. Mỗi kiểm nghiệm T sử dụng chỉ những trường hợp có giá trị đối với toàn bộ tất cả các biến được sử dụng trong bất kỳ kiểm nghiệm T test nào. Kích thước mẫu luôn không đổi
1.2. Kiểm định t hai mẫu độc lập Kiểm định này dùng cho hai mẫu độc lập, dạng dữ liệu là dạng thang đo khoảng cách hoặc tỷ lệ Đối với dạng kiểm định này, các chủ thể cần kiểm định phải được ấn định một cách ngẫu nhiên cho hai nhóm dữ liệu cần nghiên cứu sao cho bất kỳ một khác biệt nào từ kết quả nghiên cứu là do sự tác động của chính nhóm thử đó, chứ không phải do các yếu tố khác Các dữ liệu cần so sánh nằm trong cùng một biến định lượng. Để so sánh ta tiến hành nhóm các giá trị thành hai nhóm để tiến hành so sánh. Giả thuyết ban đầu cần kiểm định là giá trị trung bình của một biến nào đó thì bằng nhau giữa hai nhóm mẫu và chúng ta sẽ từ chối giả thuyết này khi mà chỉ số Sig. nhỏ hơn mức ý nghĩa (thường là 0.05)
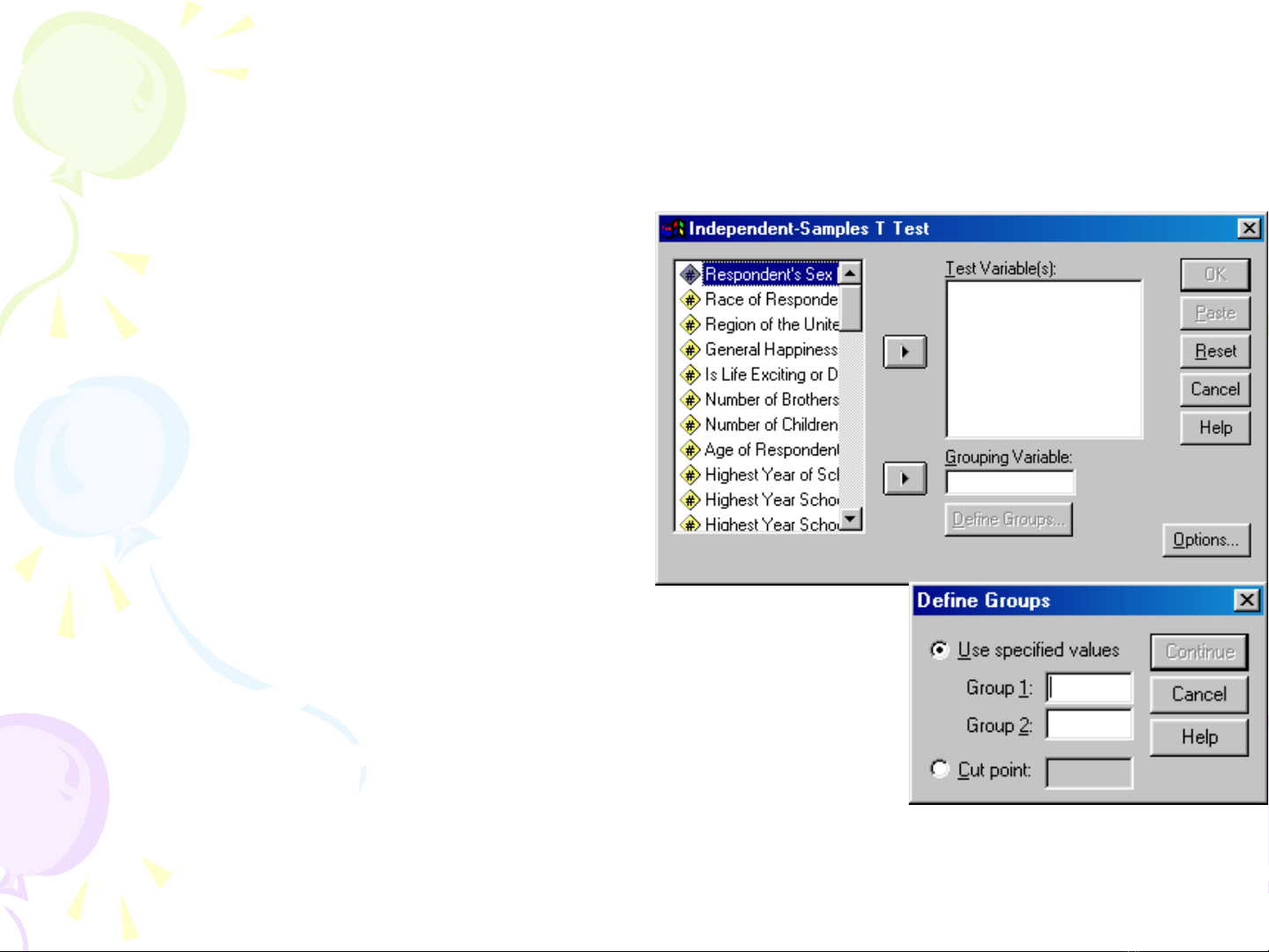
Compare means\Independent sample ttest…. Chuyển biến định lượng cần so sánh trung bình vào hộp thoại Test variable(s). Ta có thể chọn nhiều biến định lượng để so sánh. Định ra các nhóm cần so sánh với nhau (thường là biến định danh) di chuyển vào hộp thoại Gouping variable. Công cụ Define Groups… cho phép ta định ra hai nhóm cần so sánh với nhau Download trọn bộ IBM SPSS v19+crack và ebooks – articles tại http://www.mediafire.com/?1j5bcyb3asc8n
Independent sample ttest Có hai cánh định nhóm so sánh:  Sử dụng con số cụ thể, nhập hai giá trị đại diện cho hai nhóm cần so sánh trong biến vào ô group 1 và group 2  Cách thứ hai sử dụng Cut point, nhập giá tri phân cách các giá trị trong biến thành hai nhóm. Toàn bộ các trường hợp có giá trị (con số mã hóa) nhỏ hơn giá trị được nhập vào trong cut point sẽ định ra một nhóm, và toàn bộ các trường hợp có giá trị mã hóa lớn hơn hoặc bằng giá trị trong Cut point sẽ tạo ra một nhóm khác. Options để xác định độ tin cậy cho kiểm nghiệm, mặc định là 95% và cách xữ lý đối với các giá trị khuyết
1.3. Kiểm định t theo từng cặp mẫu Đây là dạng kiểm định dùng cho hai biến trong cùng một mẫu có liên hệ với nhau, dữ liệu dạng thang đó khoảng cách hoặc tỷ lệ. Nó tính toán sự khác biệt giữa các giá trị của hai biến cho mỗi trường hợp và kiểm định xem giá trị trung bình các khác biệt có khác 0 hay không. Giả thuyết ban đầu được đưa ra là giá trị trung bình của các khác biệt là bằng 0. Và ta sẽ loại bỏ giả thuyết này trong trường hợp kiểm định cho kết quả Sig. nhỏ hơn mức ý nghĩa (0.05) Điều kiện yêu cầu cho loại kiểm định này là kích cở hai mẫu so sánh phải bằng nhau. Các quan sát cho mỗi bên so sánh phải được thực hiện trong cùng những điều kiện giống nhau. Các khác biệt từ giá trị trung bình của hai mẫu phải là phân phối chuẩn hoặc số lượng mẫu đủ lớn để xấp xỉ là phân phối chuẩn
Bài toán tổng quát Bài toán tổng quát như sau: Giả sử có hai tổng thể chung: Tổng thể chung thứ nhất có các lượng biến của tiêu thức X1 phân phối theo quy luật chuẩn N ( 1, ) và tổng thể chung thứ hai có các lượng biến của tiêu thức X2 phân phối theo quy luật chuẩn N ( 2, ). Muốn so sánh sự khác nhau giữa 1 và 2 ta xét độ lệch trung bình d . Ta chưa biết d nhưng nếu có cơ sở để giả thiết rằng giá trị của nó bằng 0 , ta đua ra giả thiết thống kê H0 : d = 0. Để kiểm định giả thiết trên, từ hai tổng thể chung người ta rút ra hai mẫu phụ thuộc được hình thành bởi các cặp n quan sát độc lập của hai mẫu, từ đó tính là trung bình của các độ lệch giữa các cặp giá trị của hai mẫu di. Như vậy ta đưa bài toán so sánh về bài toán kiểm định giả thiết về giá trị trung bình đã xét ở phần I. Tuy nhiên ở đây thường không biết phương sai của các độ lệch của tổng thể chung nên thay bằng phương sai của các độ lệch của tổng thể mẫu , và dùng tiêu chuẩn kiểm định t : d 0 n t Sd
Nhận xét Phương pháp so sánh từng cặp như trên có ưu điểm hơn phương pháp so sánh hai mẫu độc lập ở chỗ: Nó không cần giả thiết gì về phương sai của hai tổng thể chung Nó thường cho kết quả chính xác hơn vì đã bỏ được các nhân tố ngoại lai ảnh hưởng đến giá trị trung bình. Tuy nhiên nhược điểm của nó là việc bố trí thí nghiệm (điều tra) phức tạp hơn, chẳng hạn trong ví dụ trên phương pháp so sánh từng cặp đòi hỏi phải trồng lúa thí nghiệm trên hai mảnh của cùng một thửa ruộng với hai loại giống khác nhau.
Compare means\Paired samples ttest Chọn hai biến ta cần so sánh di chuyển vào hộp thoại Paired Variables bằng nút mũi tên. Paired samples t test còn cho ta kết quả về mối tương quan giữa hai biến đang quan sát. Cho biết liệu hai biến này có tương quan với nhau hay không, độ tương quan và chiều tương quan (thể hiện ở bảng Paired samples correlation). Download trọn bộ IBM SPSS v19+crack và ebooks – articles tại http://www.mediafire.com/?1j5bcyb3asc8n
1.4. Phân tích phương sai một chiều (One way ANOVA) Phương pháp kiểm định sẽ mở rộng cho trường hợp so sánh trung bình của nhiều tổng thể được xây dựng trên việc xem xét các biến thiên (phương sai) của các giá trị quan sát trong nội bộ từng nhóm (mẫu) và giữa các nhóm (mẫu) với nhau. Ở đây đề cập đến phân tích phương sai một yếu tố là trường hợp chỉ có một yếu tố (biến kiểm soát) được xem xét nhằm xác định ảnh hưởng của nó đến một yếu tố khác. Yếu tố được xem xét ảnh hưởng được dùng để phân loại các quan sát thành các nhóm nhỏ khác nhau. Download trọn bộ IBM SPSS v19+crack và ebooks – articles tại http://www.mediafire.com/?1j5bcyb3asc8n
Bài toán tổng quát Giả sử ta có k tổng thể chung X1, X2, ..., Xk có phân phối chuẩn, trong đó Xi ~ N( i , ). Các giá trị trung bình i chưa biết song có cơ sở giả thiết rằng là chúng bằng nhau, ta có giả thiết cần kiểm định là H0: 1 = 2 = ... = k . Trong thống kê vấn đề trên thường được xem xét dưới góc độ sau đây: Giả sử chúng ta quan tâm tới một nhân tố X nào đó. Nhân tố X có thể xem xét ở k mức độ khác nhau. Ký hiệu Xi là hiệu quả của việc tác động của nhân tố X ở mức i . Như vậy i là hiệu quả trung bình của nhân tố X ở mức i. Chúng ta muốn biết khi cho nhân tố X thay đổi ở các mức khác nhau thì điều đó có ảnh hương hay không tới hiệu quả trung bình. Chẳng hạn, chúng ta muốn nghiên cứu ảnh hưởng của giống tới năng suất cây trồng. Nhân tố ở đây là giống, các loại giống khác nhau là các mức của nhân tố. Hiệu quả của giống lên năng suất cây trồng được đo bằng sản lượng của cây trồng. Như vậy Xi chính là sản lượng của giống i và i là sản lượng trung bình của giống i.
Trình bày số liệu tổng quát ... Các nhân tố 1 2 ...j k x11 x21 ...xi1 x1k x21 x22 ... x2k xi1... ... ... xik... k xn11 xn22 ... xnkk n nj j 1 k Tổng số T1 T2 ... Tk T Tj j 1 Trung x1 x2 xj xk x T /n bình
Các bước kiểm định Bước 1: Tính các trung bình. ni Ti x ji + Trung bình của các mẫu: j 1 xi ni ni k k nj T Tj xij + Trung bình chung: x j 1 j 1i 1 n n n Download trọn bộ IBM SPSS v19+crack và ebooks – articles tại http://www.mediafire.com/?1j5bcyb3asc8n
Các bước kiểm định Bước 2: Tính các tổng bình phương độ lệch. + Tổng bình phương chung, ký hiệu là SST (Total Sum of Squares): 2 T2 SST xij x x2ij i j i j n + Tổng bình phương do ảnh hưởng của nhân tố, ký hiệu là SSF (Sum of Squares for Factor): k 2 k Tj2 T2 SSF xj x .nj j 1 j 1 nj n + Tổng bình phương do sai số, ký hiệu là SSE (Sum of Squares for Error): 2 Tj2 SSE xij xj x2ij Từ các công thức trên, ta thấy: i j i j j nj SST = SSF + SSE
Các bước kiểm định Bước 3: Tính các phương sai tương ứng. + Phương sai do ảnh hưởng của nhân tố (hay phương sai giữa các mẫu), ký hiệu là MSF (Mean Square for Factor): SSF MSF k 1 trong đó (k 1) được gọi là bậc tự do của nhân tố. + Phương sai do sai số (hay phương sai trong các mẫu), ký hiệu là MSE (Mean Square for Error): SSE MSE n k trong đó (n k) được gọi là bậc tự do của sai số.
Các bước kiểm định Bước 4: Kiểm định giả thiết. Giả thiết H0: 1 = 2 = ... = k . H1: Tồn tại ít nhất 1 cặp j j với j j’ . Các kết quả nói trên được trình bày trong bảng sau đây và được gọi là bảng ANOVA (Analysis of Variance : Phân tích phương sai). Nguồn Tổng bình Bậc tự do Phương sai (TB Tỷ số F phương bình phương) Nhân tố SSF k 1 MSF MSF F MSE Sai số SSE n k MSE Tổng SST n 1 Người ta chứng minh được rằng nếu giả thiết H0 đúng thì tỷ số sẽ có phân phối Fisher với bậc tự do là (k 1, n k). Giả thiết H0 sẽ bị bác bỏ ở mức ý nghĩa , nếu F > F , (k1),( nk) .
Comapre means\OneWay ANOVA Chuyển các biến định lượng cần so sánh sang hộp thoại Dependent List. Lựa biến kiểm soát tức là biến độc lập (yêu cầu phải có ba giá trị trở lên trong biến kiểm soát này) chuyển biến kiểm soát vào hộp thoại Factor, Biến kiểm soát này cho phép ta phân các giá trị trung bình theo từng nhóm để kiểm định. Thao tác đến đây cho phép ta đưa ra kết luận liệu các trung bình của các nhóm có bằng nhau hay không. Download trọn bộ IBM SPSS v19+crack và ebooks – articles tại http://www.mediafire.com/?1j5bcyb3asc8n
Để tiến hành kiểm định so sánh sự khác biệt giữa các nhóm với nhau ta lựa chọn công cụ Post Hoc và lựa chọn các phương pháp kiểm định thích hợp Đối với trường hợp giả thuyết về sự cân bằng phương sai giữa các mẫu không được chấp nhận ta sẽ sử dụng các phương pháp kiểm định sau để tiến hành so sánh giá trị trung bình giữa các nhóm:Tamhane’s T2, Dunnett’s T3, Games Howell, Dunnett’s C
phương pháp kiểm định thống kê so sánh các trung bình mẫu  The least significant difference (LSD) là phép kiểm định tương đương với việc sử dụng phương pháp kiểm định t riêng biệt cho toàn bộ các cặp trong biến. Yếu điểm của phương pháp này là nó không chỉnh lý độ tin cậy cho tương thich với việc kiểm định cho nhiều so sánh cùng một lúc. Do đó dẫn đến độ tin cậy không cao.  Phương pháp kiểm định Bonferroni và Tukey’s honestly significant difference thì được sử dụng cho hầu hết các kiểm định so sánh đa bội. Kiểm định Sidak’s t test cũng được sử dụng tương tư như phương pháp Bonferroni tuy nhiên nó cung cấp những giới hạn chặt chẻ hơn. Khi tiến hành kiểm định một số lượng lớn các cặp trung bình Tukey’s honestly significant difference test sẽ có tác động mạnh hơn là Bonferroni test. Và ngược lại Bonferroni thì thích hợp hơn cho các kiểm định có số lượng cặp so sánh ít.