!"#$
!!"#$
!!"%$$ !!&
'()*+,($(-+"+$
($+#)$
.
/ ( ) # $ 0
.
$0
#$0
1
.
23 # ) 4 *+ ($ (- +
# ) ) . 5 +
#)0
0
"
#)$0
0
.6(7/(+8+"
#$.
+ ( )" 9
9:#*+;
6 !!6,0
"0
1
.
6 (- - 6
1
"
6
<
" &"
6
.
($6
1
"
6
<
"&"
6
9+
+0
3#$:
!!9+:).
29(#="+
>
;
?>
@0
A#(-+"(
.B#7#);
C>
;0
.
C>
;$0
.
%"&'()*
%"!)+,-
!"!"#$%&
"
'
(
D9($(-+%9":
E)
3,9
(#=.:($
9+#"/();
0
;
,90
1
;
!.%./0'(1
0.,
%
23
(#44+1
'($99+:#3,9
(- - % 9 "
6
@
D D% 57 # 9+ : :4 ,9
D D% 57. 59 9+ 3 #
9A.
)%*+
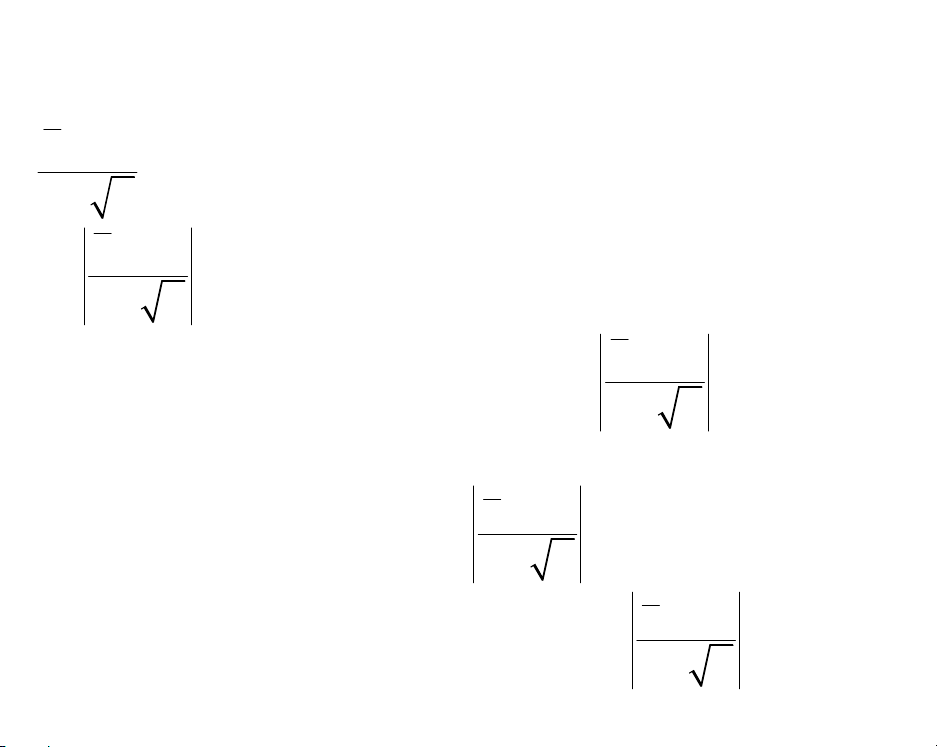
)0
"
. # !!
6
@
D D% 57" ,3 ,$#
6
@
F
@<
:#,9:1G.29HI
9 :" E
6
@
F
@<
7
7:#+",9(-+%
9J
:
@
F
@<
.!,9($
(- + % 9 " #
:
@
K
F
@<
3
