
Chương 3: Thống kê xác suất ứng dụng
trong tính toán thủy văn
THUỶ VĂN CÔNG TRÌNH
Khoa Thuỷ văn – Tài nguyên nước
Bộ môn Thuỷ văn – Tài nguyên nước
1

3.1 Khái niệm về xác suất và tần suất
1. Các khái niệm cơ bản
Phép thử: Thc hiện mt thử nghiệm va quan sát kt quả thc
hiện đối với mt hiện tượng ngẫu nhiên nào đó trong cùng
mt điều kiện nhất định.
Kt quả của mt phép thử ngẫu nhiên gọi là bin cố ngẫu
nhiên, hoặc nói ngắn gọn là bin cô / bin cố cơ bản. Tp hợp
cc bin cô có thê xy ra trong mt php thư gọi l không gian
bin cô.
2

3.1 Khái niệm về xác suất và tần suất
Phân loại bin cố
Bin cố chắc chắn: là bin cố nhất định phải xuất hiện trong
mt phép thử.
Bin cố không thể có: là bin cố không thể xuất hiện trong
mt phép thử.
Bin cố đc lp: là bin cố mà s xuất hiện của nó không phụ
thuc vào s xuất hiện của các bin cố khác
Bin cố phụ thuc: là bin cố mà s xuất hiện của nó phụ
thuc vào s xuất hiện của bin cố khác
3
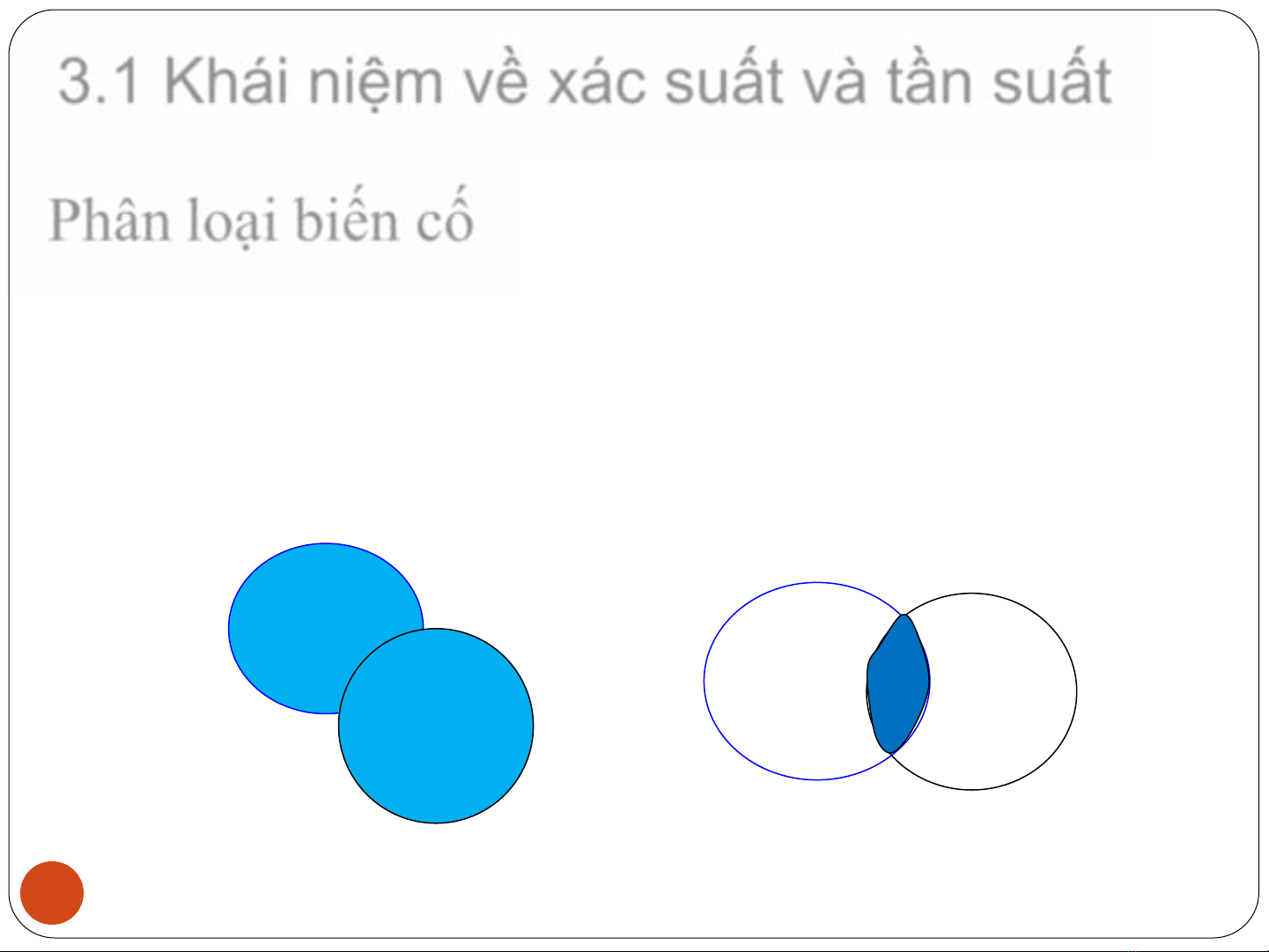
3.1 Khái niệm về xác suất và tần suất
Phân loại bin cố
Bin cố tổng: bin cố C được gọi là bin cố tổng của hai bin cố A
và B nu hoặc A xuất hiện, hoặc B xuất hiện, hoặc cả A và B cùng
xuất hiện đều dẫn đn sư xuất hiện của C.
Bin cố tích: Bin cố C được gọi là bin cố tích của hai bin cố A
và B khi va ch khi ca 2 bin cố A và B đng thi xuất hiện tạo nên.
4
A
B
A
B
C=A+B C=A.B

3.1 Khái niệm về xác suất và tần suất
Xác suất
Định nghĩa cổ điển: Xác suất xuất hiện của mt bin cố
A nào đó bằng tỷ số giữa số bin cố cơ bản thun lợi
cho A xuất hiện trên tổng các bin cố cơ bản của không
gian bin cố.
Công thức tính xác suất của bin cố A theo định nghĩa cô
điển:
n là tổng số các bin cố cơ bản của không gian bin cố đang xét;
m là số bin cố cơ bản thun lợi cho bin cố A xuất hiện.
5
n
m
AP )(


























