CH NG 2: TĨNH H C L U CH TƯƠ Ọ Ư Ấ
CH NG 2: TĨNH H C L U CH TƯƠ Ọ Ư Ấ
2.1. KHÁI NI MỆ
2.1. KHÁI NI MỆ
2.2. ÁP SU T TH Y TĨNHẤ Ủ
2.2. ÁP SU T TH Y TĨNHẤ Ủ
2.3.
2.3. PH NG TRÌNH VI PHÂN C B N TĨNH H C ƯƠ Ơ Ả Ọ
PH NG TRÌNH VI PHÂN C B N TĨNH H C ƯƠ Ơ Ả Ọ
L U CH T Ư Ấ
L U CH T Ư Ấ
2.4
2.4. L U CH T TĨNH TRONG TR NG TR NG L CƯ Ấ ƯỜ Ọ Ự
. L U CH T TĨNH TRONG TR NG TR NG L CƯ Ấ ƯỜ Ọ Ự
2.5
2.5. TĨNH T NG Đ IƯƠ Ố
. TĨNH T NG Đ IƯƠ Ố
1
2.1. KHÁI NI MỆ
2.1. KHÁI NI MỆ
Tĩnh l c h c ự ọ LC nghiên c uứ LC tr ng thái ở ạ CB :
• Không có CĐ t ng đ i gi a các ph n t .ươ ố ữ ầ ử
• Không có thành ph n ng su t ti p.ầ ứ ấ ế
•L c t ng tác gi a ự ươ ữ LC và thành r n ho c bên trong ắ ặ
LC vuông góc v i m t phân chiaớ ặ .
Khi LC chuy n đ ng nh ng tĩnh so m t h tr c ể ộ ư ộ ệ ụ
nào đó thĩ v n xem là tĩnh.ẫ
LC cân b ng: ằ
T ng các thành ph n l c tác d ng theo m i ph ng ổ ầ ự ụ ọ ươ
b ng không.ằ
T ng momen c a các l c đ i v i m t đi m b t kỳ ổ ủ ự ố ớ ộ ể ấ
b ng khôngằ.
2
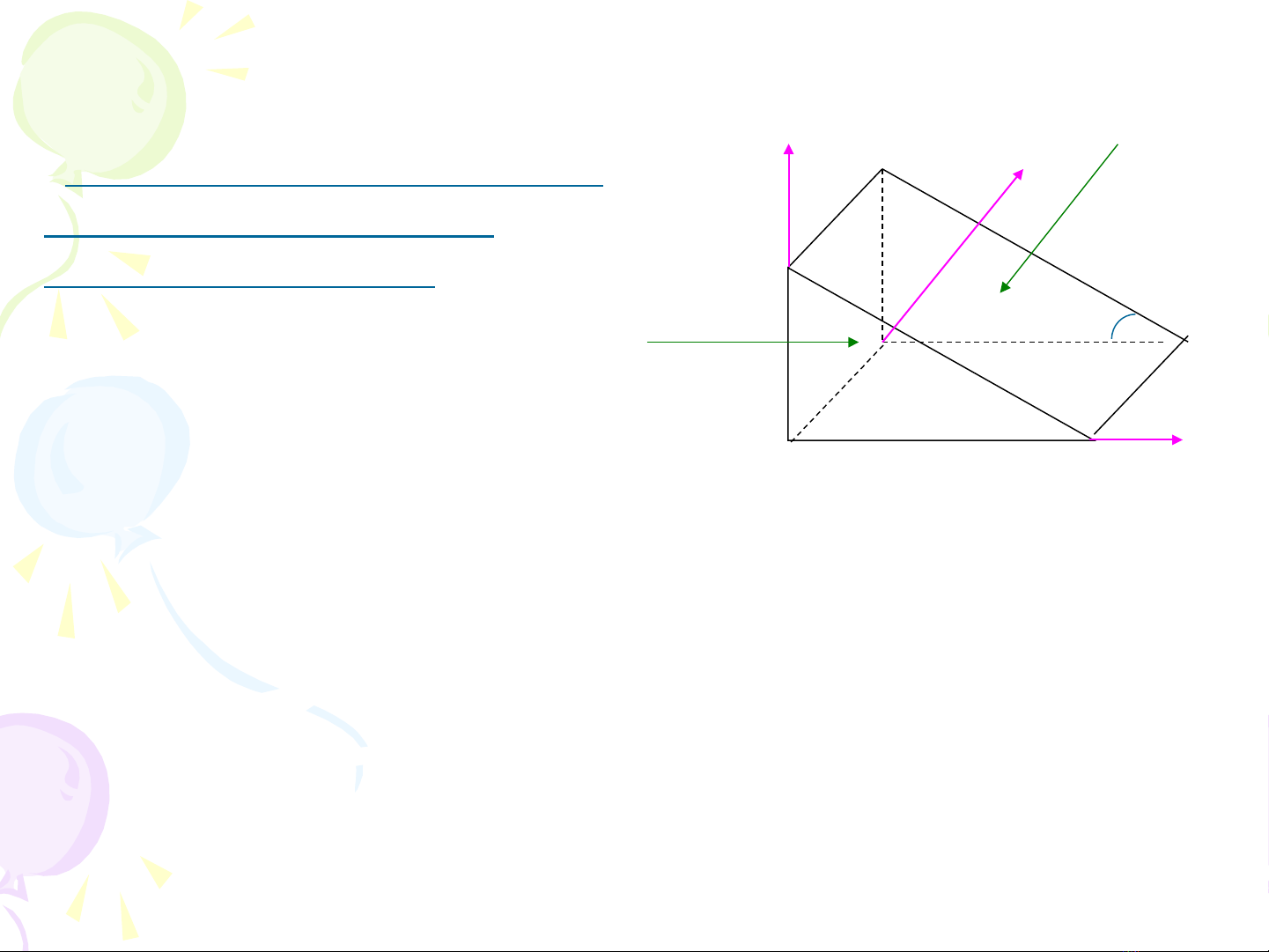
2.2.1. Đ nh nghĩaị
Áp su t th y tĩnh là l c pháp tuy n tác d ng lên m t đ n v di n ấ ủ ự ế ụ ộ ơ ị ệ
tích.
AS th y tĩnh t i m t đi m:ủ ạ ộ ể
2.2.2. Tính ch tấ
AS th y tĩnh tác d ng th ng góc và h ng vào ủ ụ ẳ ướ
trong di n tích ch u l cệ ị ự .
Giá tr ịAS th y tĩnh t i m t đi mủ ạ ộ ể
không ph thu c h ng đ t c a di n tích ch u l cụ ộ ướ ặ ủ ệ ị ự .
F∆
A
∆
A
F
p
A
∆
∆
=
→∆
0
lim
2.2.
2.2. ÁP SU T TH Y TĨNHẤ Ủ
3
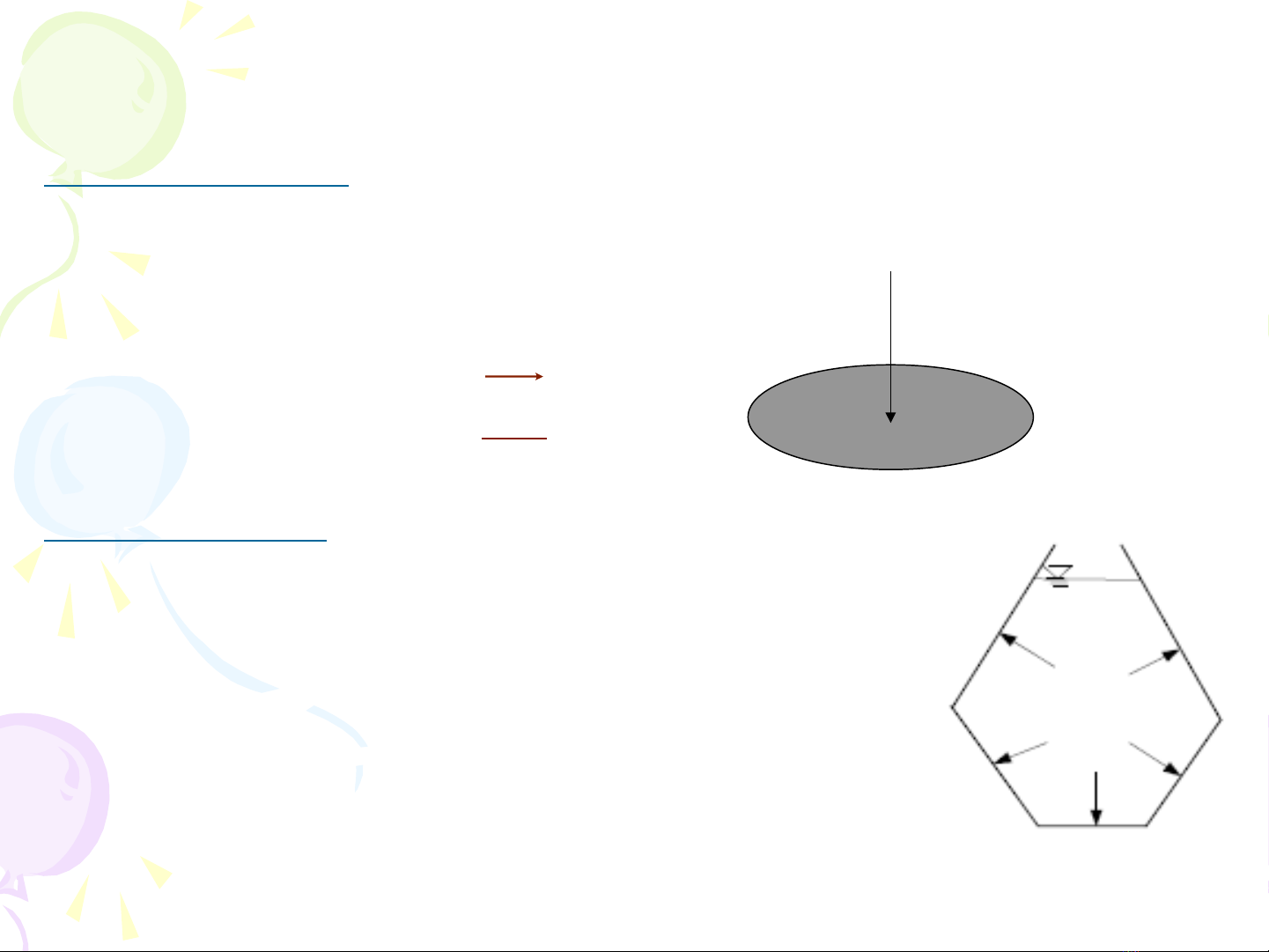
* Ch ng minh: Xét s cân b ngứ ự ằ
c a 1 vi phân th tích ủ ể LC
hình lăng tr tam giácụ
L c do pựx tác d ng lên m t ụ ặ
ABCD chi u lên Ox: pếx. δy.δz
L c do pựs tác d ng lên m t ụ ặ
BCEF chi u lên Ox:ế
-ps .δy.δs.sinθ = -ps .δy. δs. δz/ δs = -ps .δy. δz
F là l c kh i đ n v , l c kh i tác d ng lên ph n t ự ố ơ ị ự ố ụ ầ ử LC
chi u lên Ox là:ế
Do l u ch t cân b ng: pư ấ ằ x.δy.δz-ps .δy.δz+(1/2)ρ.Fx
.δx.δy.δz =0
px - ps + (1/2)ρ.Fx .δx = 0 . Khi δx -> 0 px = ps
δs
δz
δ
x
δ
y
px
ps
A
B
C
D
F
E
z
x
y
θ
O
2.2. ÁP SU T TH Y TĨNHẤ Ủ
2.2. ÁP SU T TH Y TĨNHẤ Ủ
4
T ng t cho ph ng z: pươ ự ươ z= ps
=> px = pz = ps
2.2.3. Th nguyên và đ n v c a áp su tứ ơ ị ủ ấ
Th nguyên c a áp su t:ứ ủ ấ
Đ n v c a áp su t :ơ ị ủ ấ
+ H SI: N/mệ2 = Pa
+ H khác: 1at=1kgf/cmệ2 = 10m n c = ướ
735,5mmHg = 98100 Pa (N/m2)
2.2. ÁP SU T TH Y TĨNHẤ Ủ
2.2. ÁP SU T TH Y TĨNHẤ Ủ
2
.
][
][
][
−
==
LF
A
F
p
5