zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Kỹ Thuật - Công Nghệ

» Điện - Điện tử

Bài giảng Xử lý tín hiệu số: Chương 2 - ThS. Nguyễn Thị Phương Thảo

Chia sẻ: Bạch Khinh Dạ Lưu | Ngày: | Loại File: PDF | Số trang:74

Báo xấu

40
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Xử lý tín hiệu số: Chương 2 - ThS. Nguyễn Thị Phương Thảo cung cấp cho học viên các kiến thức về hệ thống và tín hiệu rời rạc thời gian; tín hiệu rời rạc thời gian; hệ thống rời rạc thời gian; hệ thống tuyến tính bất biến; phương trình sai phân tuyến tính hệ số hằng;... Mời các bạn cùng tham khảo chi tiết nội dung bài giảng!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Xử lý tín hiệu số: Chương 2 - ThS. Nguyễn Thị Phương Thảo

Hệ thống và tín hiệu rời rạc thời gian Bài giảng: Xử lý tín hiệu số
Chương 2. Tín hiệu và hệ thống rời rạc thời gian 1. Tín hiệu rời rạc thời gian 2. Hệ thống rời rạc thời gian 3. Hệ thống tuyến tính bất biến 4. Phương trình sai phân tuyến tính hệ số hằng
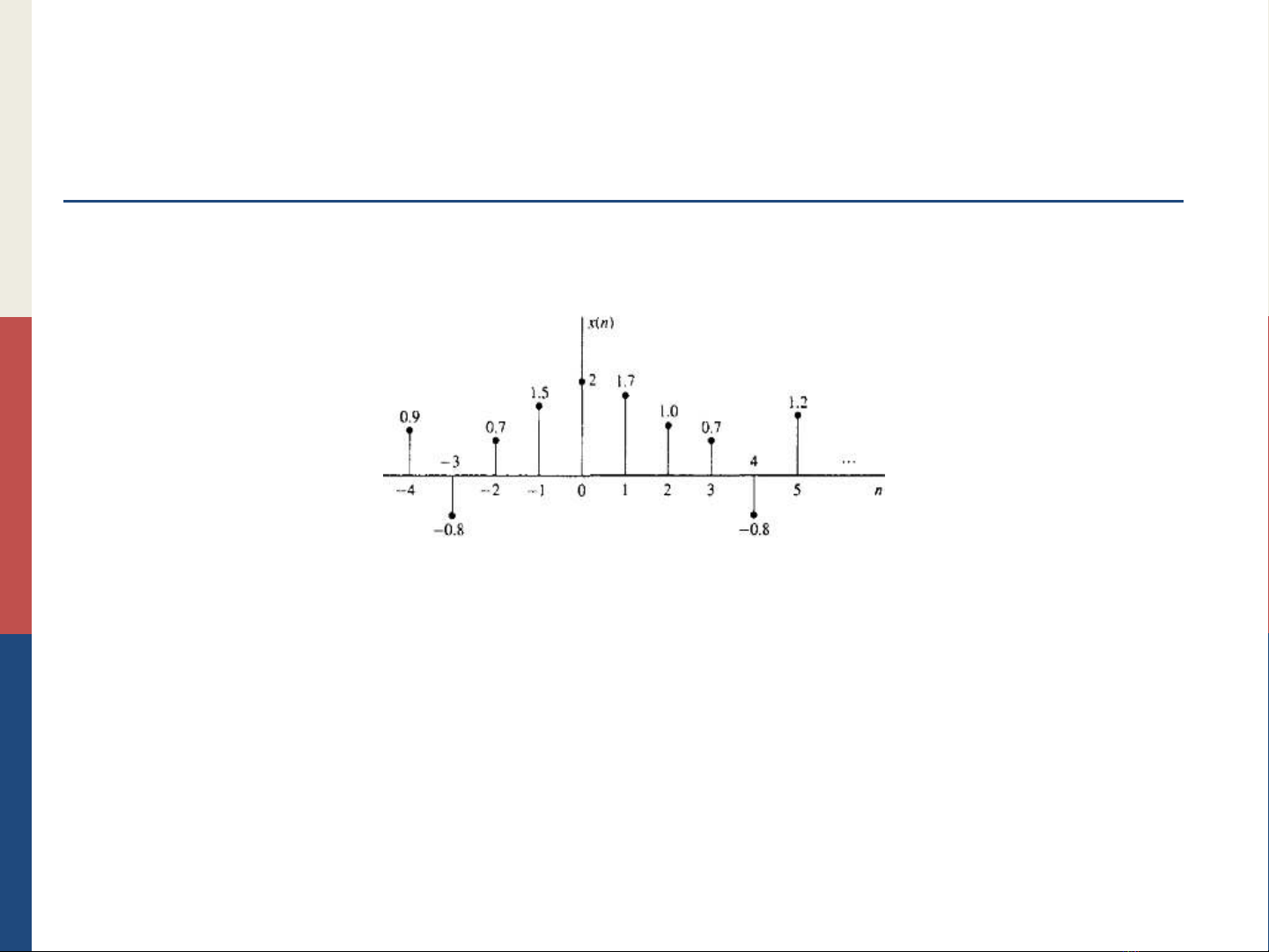
2.1 Tín hiệu rời rạc thời gian Định nghĩa a. Định nghĩa: Tín hiệu rời rạc là hàm của biến độc lập có giá trị nguyên  Ký hiệu: x(n) với n thuộc Z  Chú ý:  Tín hiệu x(n) thể được tạo ra bằng cách lấy mẫu tín hiệu x(t) với chu kỳ lấy mẫu ts  x(n) có thể có giá trị thực hoặc phức  Với n không nguyên không phải 𝑥(𝑛) = 0, mà chỉ đơn giản là ta ko xét đến giá trị của x(n)  n có thể có giá trị từ -∞  +∞
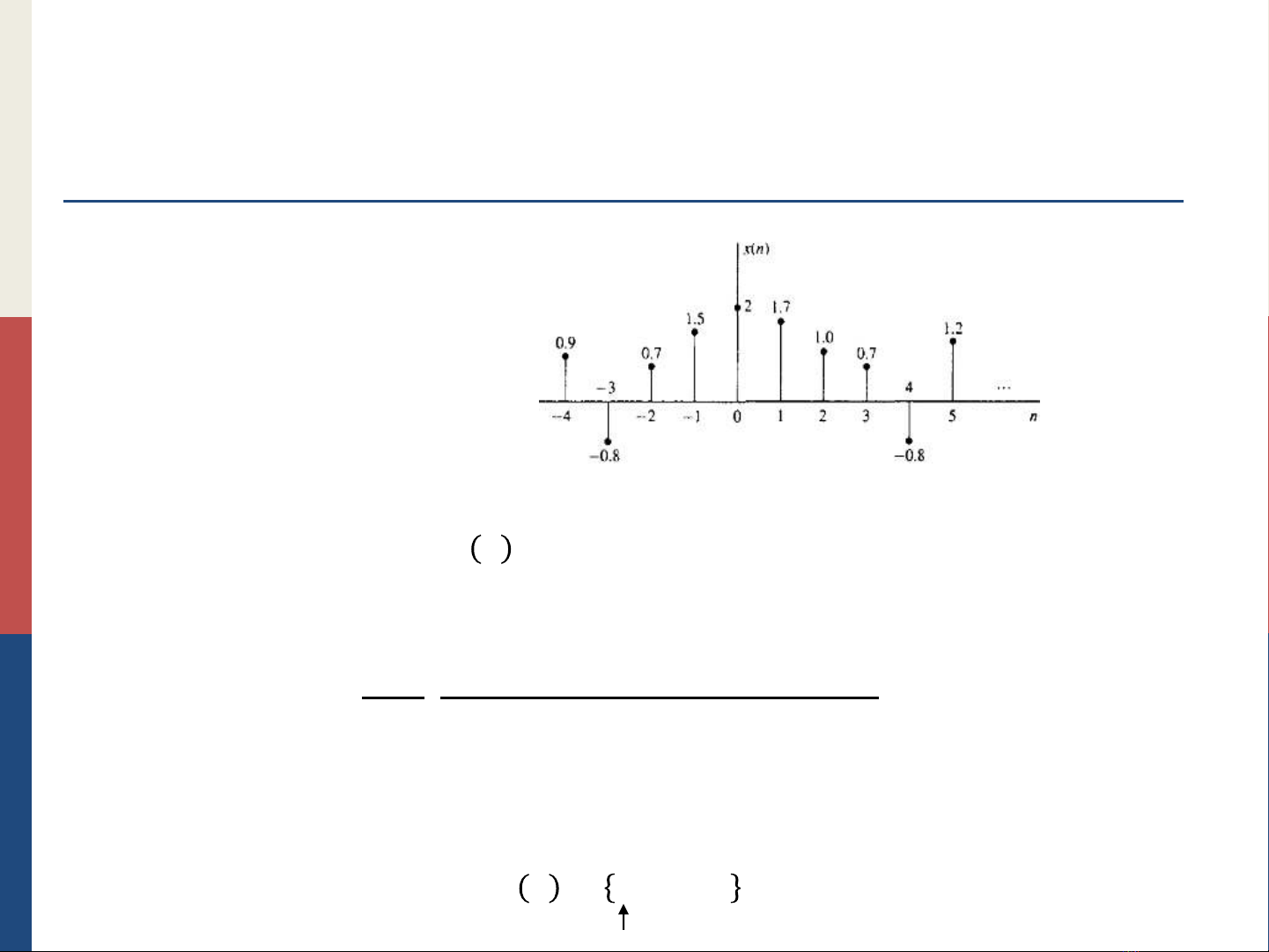
Định nghĩa (tiếp) b. Biểu diễn tín hiệu  Biểu diễn bằng đồ thị  Biểu diễn dưới dạng hàm: 1, 𝑣ớ𝑖 𝑛 = 1,3 𝑥 𝑛 = 4, 𝑣ớ𝑖 𝑛 = 2 0, 𝑐ò𝑛 𝑙ạ𝑖  Biểu diễn dưới dạng liệt kê: 𝑛 … −2 −1 0 1 2 3 4 5 … 𝑥(𝑛) … 0 0 0 1 4 1 0 0 …  Biểu diễn dưới dạng dãy: Gốc thời gian (𝑛 = 0) của một tín hiệu hoặc dãy vô hạn được chỉ thị bởi ký hiệu ↑ như sau: 𝑥 𝑛 = 0,1,4,1,0
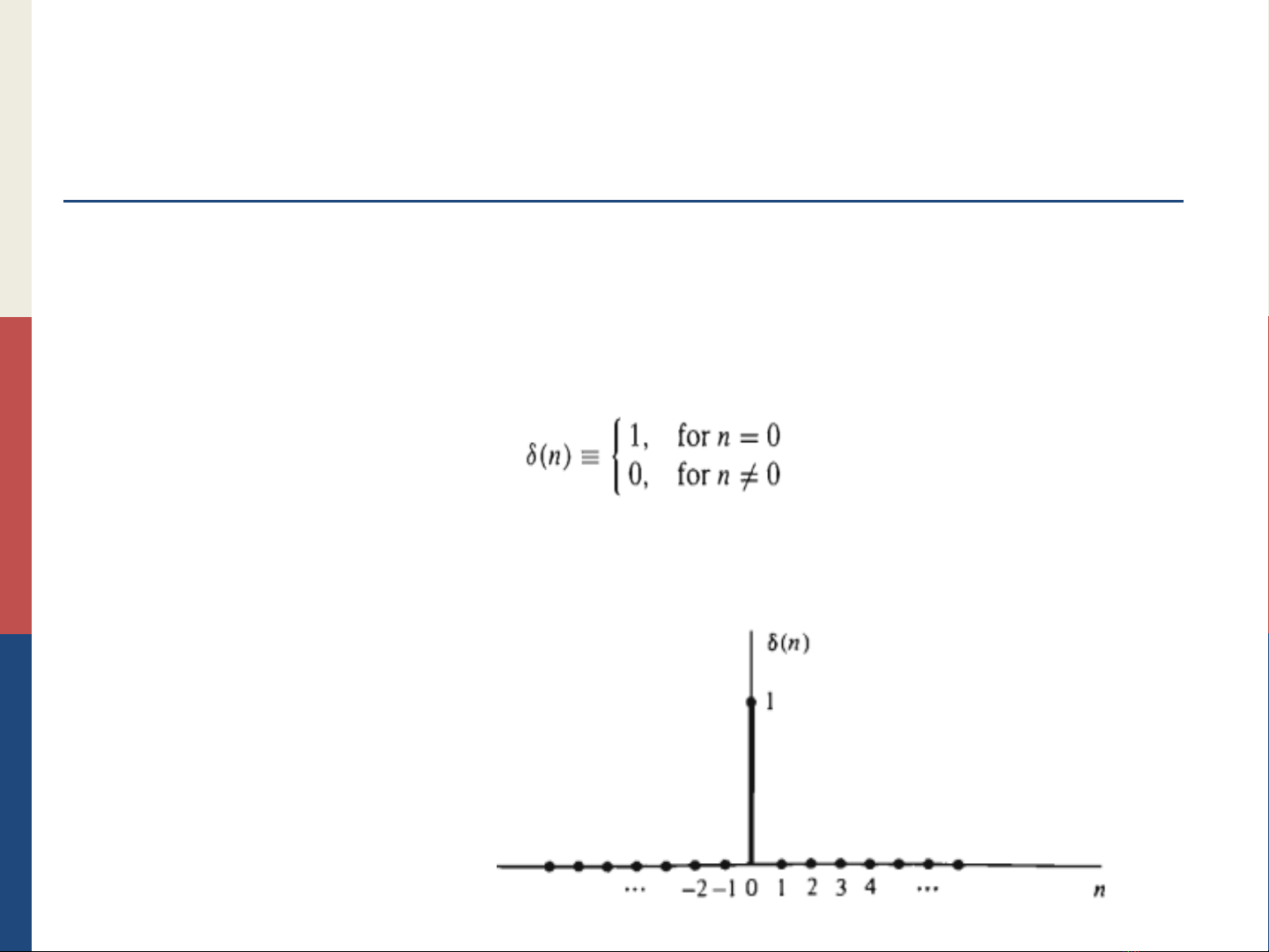
2.1.1 Một vài tín hiệu cơ bản Một số dạng tín hiệu cơ bản thường xuyên xuất hiện và đóng vai trò quan trọng a. Dãy xung đơn vị: ký hiệu 𝛿(𝑛) Dãy xung đơn vị bằng 1 với 𝑛 = 0 và bằng 0 với mọi n còn lại. Biểu diễn bằng đồ thị
2.1.1 Một vài tín hiệu cơ bản b. Dãy nhảy đơn vị: ký hiệu là 𝑢 𝑛 Dãy nhảy đơn vị bằng 1 với 𝑛 ≥ 0 và bằng 0 với n còn lại. Biểu diễn bằng đồ thị
2.1.1 Một vài tín hiệu cơ bản c. Dãy chữ nhật: ký hiệu là rect N 𝑛 1 𝑣ớ𝑖 0 ≤ 𝑛 ≤ 𝑁 − 1 rect N 𝑛 = 0 𝑣ớ𝑖 𝑛 𝑐ò𝑛 𝑙ạ𝑖 Dãy chữ nhật bằng 1 với 0 ≤ 𝑛 ≤ 𝑁 − 1 và bằng 0 với n còn lại. Biểu diễn bằng đồ thị
2.1.1 Một vài tín hiệu cơ bản d. Dãy dốc đơn vị: ký hiệu là 𝑢𝑟 (𝑛) Dãy dốc đơn vị bằng 𝑛 với 𝑛 ≥ 0 và bằng 0 với 𝑛 còn lại. Biểu diễn bằng đồ thị
2.1.1 Một vài tín hiệu cơ bản e. Dãy hàm số mũ là dãy có dạng 𝑥(𝑛) = 𝑎𝑛 với mọi n (a là số thực)
2.1.2. Phân loại tín hiệu rời rạc thời gian  Phân tích đặc điểm của tín hiệu có ý nghĩa quan trọng trong việc lựa chọn và sử dụng các công cụ toán học để xử lý tín hiệu.  Mục tiêu của phần này là phân loại tín hiệu dựa trên một số đặc điểm nhất định a) Dãy năng lượng và dãy công suất - Năng lượng của một tín hiệu: +∞ 𝐸= 𝑥 𝑛 2 𝑛=−∞ - Năng lượng của tín hiệu có thể hữu hạn hoặc vô hạn - Nếu E là hữu hạn (có nghĩa là 0 < E < ∞), thì x(n) được gọi là dãy năng lượng.
2.1.2. Phân loại tín hiệu rời rạc thời gian a. Dãy năng lượng và dãy công suất (tiếp) - Công suất trung bình của tín hiệu rời rạc thời gian được xác định như sau: +𝑁 1 2 𝑃 = lim 𝑥 𝑛 𝑁→∞ 2𝑁 + 1 𝑛=−𝑁 - Nếu ta định nghĩa năng lượng của 𝑥(𝑛) trong khoảng hữu hạn – 𝑁 ≤ 𝑛 ≤ 𝑁 như sau: +𝑁 𝐸𝑁 = 𝑥 𝑛 2 𝑛=−𝑁 - Vậy, năng lượng của tín hiệu được viết lại như sau: 𝐸 = lim 𝐸𝑁 𝑁→∞ và công suất trung bình của tín hiệu: 1 𝑃 = lim 𝐸𝑁 𝑁→∞ 2𝑁 + 1 - Nếu P hữu hạn (và khác 0), tín hiệu được gọi là tín hiệu công suất.
2.1.2. Phân loại tín hiệu rời rạc thời gian b. Dãy tuần hoàn và dãy không tuần hoàn  Tín hiệu x(n) tuần hoàn với chu kỳ N (N>0) khi và chỉ khi x(n + N) = x(n) với mọi n  Giá trị nhỏ nhất của N được gọi là chu kỳ cơ bản  Nếu không tồn tại giá trị nào của N thỏa mãn công thức trên thì tín hiệu x(n) là dãy không tuần hoàn
2.1.2. Phân loại tín hiệu rời rạc thời gian c. Dãy chẵn và dãy lẻ  Một tín hiệu thực 𝒙(𝒏) được gọi là dãy chẵn nếu: 𝑥 −𝑛 = 𝑥 𝑛  Tín hiệu x(n) được gọi là dãy lẻ nếu: 𝑥(−𝑛) = −𝑥 𝑛
2.1.2. Phân loại tín hiệu rời rạc thời gian c. Dãy chẵn và dãy lẻ (tiếp)  Một tín hiệu 𝑥(𝑛) bất kỳ đều có thể được biểu diễn dưới dạng tổng của 2 tín hiệu chẵn và lẻ  Cụ thể, với tín hiệu bất kỳ x(n):  Ta có 1 tín hiệu chẵn được sinh ra từ x(n) 1 𝑥𝑐 (𝑛) = 𝑥 𝑛 + 𝑥 −𝑛 2  1 tín hiệu lẻ được sinh ra từ x(n) 1 𝑥𝑙 (𝑛) = 𝑥(𝑛)– 𝑥(−𝑛) 2  Cộng 2 tín hiệu trên ta được: 𝒙(𝒏) = 𝒙𝒄 (𝒏) + 𝒙𝒍 (𝒏)
2.1.3 Một số phép toán a) Dịch tín hiệu trên miền thời gian(trễ hay tới trước): dịch tín hiệu 𝑥(𝑛) trên miền thời gian bằng cách thế biến số độc lập 𝑛 bằng (𝑛 − 𝑘), với 𝑘 là số nguyên • 𝑘 là số nguyên dương thì ta được tín hiệu trễ 𝑘 mẫu so với 𝑥(𝑛)  dịch phải 𝒌 đơn vị • 𝑘 là số nguyên âm thì ta có tín hiệu sớm 𝑘 mẫu so với 𝑥(𝑛)  dịch trái k đơn vị Ví dụ: vẽ 𝑥(𝑛 − 3) và 𝑥(𝑛 + 2), với 𝑥(𝑛) như sau:
2.1.3 Một số phép toán b) Phản xạ (đối xứng) tín hiệu: thế biến độc lập 𝑛 thành − 𝑛, ta thu được tín hiệu 𝑥(−𝑛) lấy đối xứng với tín hiệu 𝒙(𝒏) qua gốc tọa độ Ví dụ: Vẽ đồ thị biểu diễn tín hiệu 𝑥(−𝑛) và 𝑥(−𝑛 + 2), với 𝑥(𝑛) như sau
2.1.3 Một số phép toán c) Phép co giãn thời gian Thay biến số độc lập của tín hiệu 𝑥(𝑛) bằng 𝑎𝑛, với 𝑎 là số nguyên, ta được tín hiệu 𝑥(𝑎𝑛) Ví dụ: Cho tín hiệu 𝑥(𝑛) như hình dưới, vẽ đồ thị biểu diễn tín hiệu 𝑦(𝑛) = 𝑥(2𝑛)
2.1.3 Một số phép toán d) Phép cộng, phép nhân và co giãn biên độ dãy: các phép toán tác động lên biên độ của tín hiệu  Phép co giãn biên độ của tín hiệu theo hằng số A được thực hiện bằng cách nhân giá trị của mỗi mẫu tín hiệu với A. 𝑦 𝑛 = 𝐴𝑥 𝑛 − ∞ < 𝑛 < +∞  Phép cộng hai tín hiệu 𝑥1(𝑛) và 𝑥2(𝑛) thu được tín hiệu 𝑦(𝑛), với mọi giá trị của 𝑦(𝑛) tại một thời điểm bằng tổng giá trị của 2 tín hiệu tương ứng 𝑦 𝑛 = 𝑥1 𝑛 + 𝑥2 𝑛 − ∞ < 𝑛 < +∞  Phép nhân hai tín hiệu cho ta một tín hiệu có giá trị các mẫu bằng tích giá trị hai mẫu tương ứng 𝑦 𝑛 = 𝑥1 𝑛 𝑥2 𝑛 − ∞ < 𝑛 < +∞
Ví dụ: cho hai tín hiệu 𝑥1 𝑛 = {1,2,3,4} và 𝑥2 𝑛 = 𝑟𝑒𝑐𝑡4 (𝑛 + 1). Tính: a. 3𝑥1 𝑛 b. 𝑥1 𝑛 + 2𝑥2 (𝑛) c. 𝑥12 (𝑛) d. 𝑥1 𝑛 . 𝑥2 (𝑛)
Bài tập 1. Biểu diễn các tín hiệu sau: a. 𝛿(𝑛 − 3), 𝑟𝑒𝑐𝑡4 (𝑛 + 1), 𝑢(−𝑛), 𝑢(−𝑛 + 2), 𝑢(−𝑛 − 3) 1 𝑛−3 b. 2𝑛 𝑢 𝑛 , 𝑟𝑒𝑐𝑡3 (𝑛 − 3) 2 2. Cho tín hiệu 𝑥1 (𝑛) và 𝑥2 (𝑛) như hình dưới đây, xác định và biểu diễn các t/h sau dưới dạng đồ thị a. 𝑥1 𝑛 𝑟𝑒𝑐𝑡5 (𝑛) b. 𝑥1 (𝑛). 𝑥2 (𝑛) c. 𝑥2 (2𝑛) d. 𝑥1 (𝑛) + 2𝑥2 (𝑛) e. 𝑥1 (−𝑛 + 3) f. 𝑥1 𝑛 + 𝑥2 𝑛 𝛿(𝑛 − 2) 3. Biểu diễn các tín hiệu trong câu 2 theo 𝛿(𝑛 − 𝑘)

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí

65 tài liệu

2430 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.