
Xửlý tín hiệu sốvà ứng dụng
Tín hiệu và hệthống rời rạc
Nguyễn Công Phương

Nội dung
I. Khái niệm chung
II. Tín hiệu và hệthống rời rạc
III. Lọc số
IV. Vi xửlý tín hiệu số
V. Một sốví dụ ứng dụng
sites.google.com/site/ncpdhbkhn 2

Tín hiệu và hệthống rời rạc
1. Lấy mẫu tín hiệu rời rạc
2. Biểu diễn tín hiệu rời rạc
3. Các hệthống rời rạc
4. Biếnđổi Fourier rời rạc của tín hiệu rời rạc tuần hoàn
5. Biếnđổi Fourier rời rạc của tín hiệu có độ dài hữu hạn
6. Biếnđổi Fourier nhanh
7. Các hàm cửa sổ
sites.google.com/site/ncpdhbkhn 3
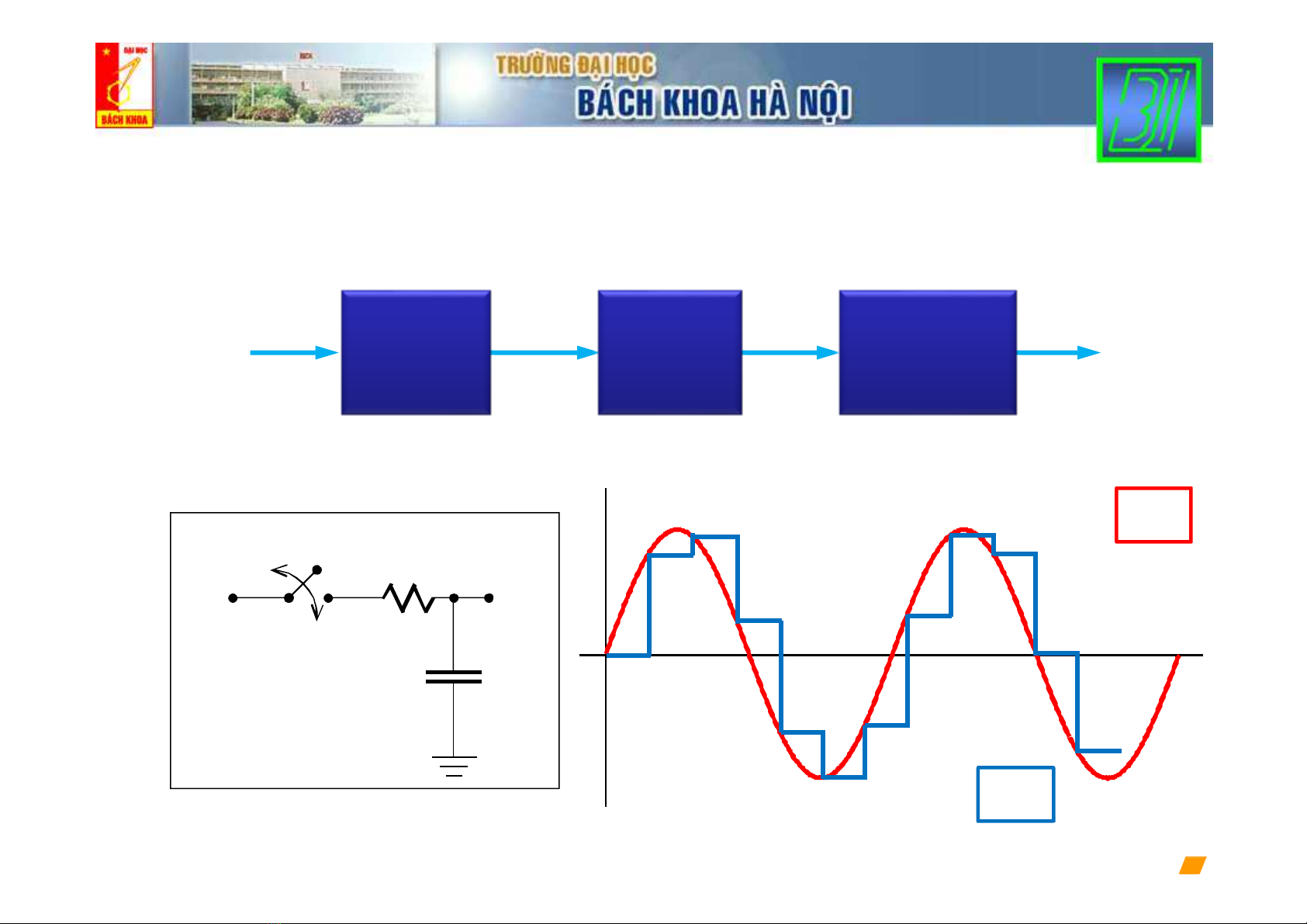
Lấy mẫu tín hiệu rời rạc (1)
sites.google.com/site/ncpdhbkhn 4
Bộbiếnđổi
tương tự/số
Fs= 1/T
( )
a
x t
[ ]
q
x n
Bộlọc
tiền xửlý
Ha(jΩ)
( )
c
x t
Lấy mẫu
& giữ
Fs= 1/T
0
t
v
x t
( )
r
x t
( )
v
x t
( )
r
x t
( )
R
C
Giữ
Lấy mẫu
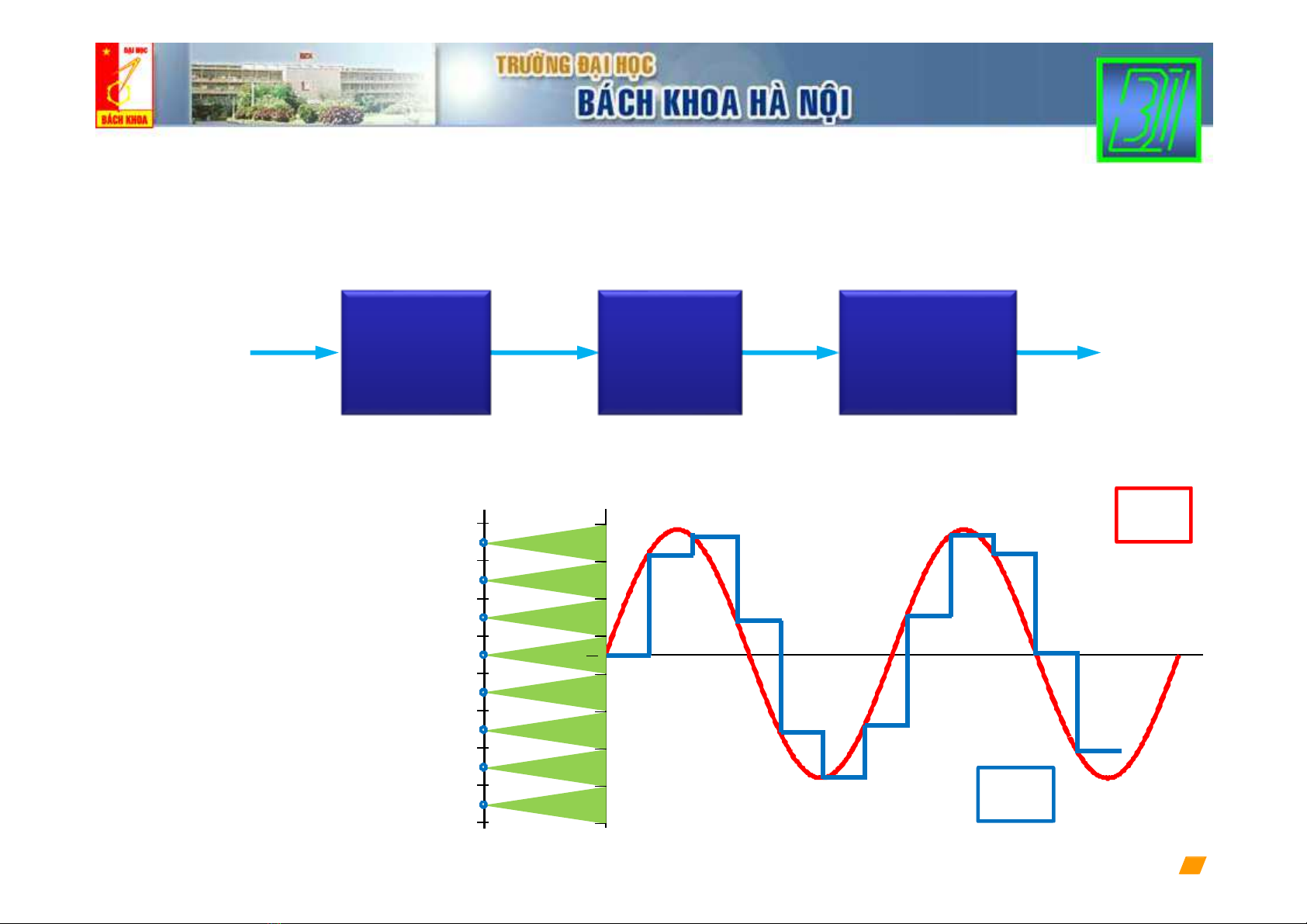
Lấy mẫu tín hiệu rời rạc (2)
sites.google.com/site/ncpdhbkhn 5
Bộbiếnđổi
tương tự/số
Fs= 1/T
( )
a
x t
[ ]
q
x n
Bộlọc
tiền xửlý
Ha(jΩ)
( )
c
x t
Lấy mẫu
& giữ
Fs= 1/T
0
t
v
x t
( )
r
x t
( )
011
010
001
000
111
110
101
100
























![Đề thi cuối học kì 2 môn Cấu trúc dữ liệu và giải thuật [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251014/lakim0906/135x160/89711760416179.jpg)

