
www.saosangsong.com.vn Năm học 2009-2010 1
NHÁY D 2009.
Thời gian làm bài : 180 phút
Câu 1 (2 điểm ). Cho hàm số y = x4 – (2m – 1) x2 + 4m – 3 (1)
a) Khảo sát hàm số và vẽ đồ thị khi m = 2 .
b) Tìm m để đồ thị hàm số (1) cắt đường thẳng y = 3 tại 4 điểm đều có hoành độ < 2.
Câu 2 (2 điểm ) :
1. Giải phương trình : 2
3 sin 4x 2cos3xcosx - 2sin (x )
π
++
+ 1 = 0
2. Giải hệ: 2
2
(x )(x 2) 12 0
80
(x ) 4 0
(x )
yy
yy
−++−=
⎧
⎪
⎨++− =
⎪−
⎩
Câu 3 (1 điểm ). Tính tích phân I = ln 3
x
0
x
1
d
e
+
∫
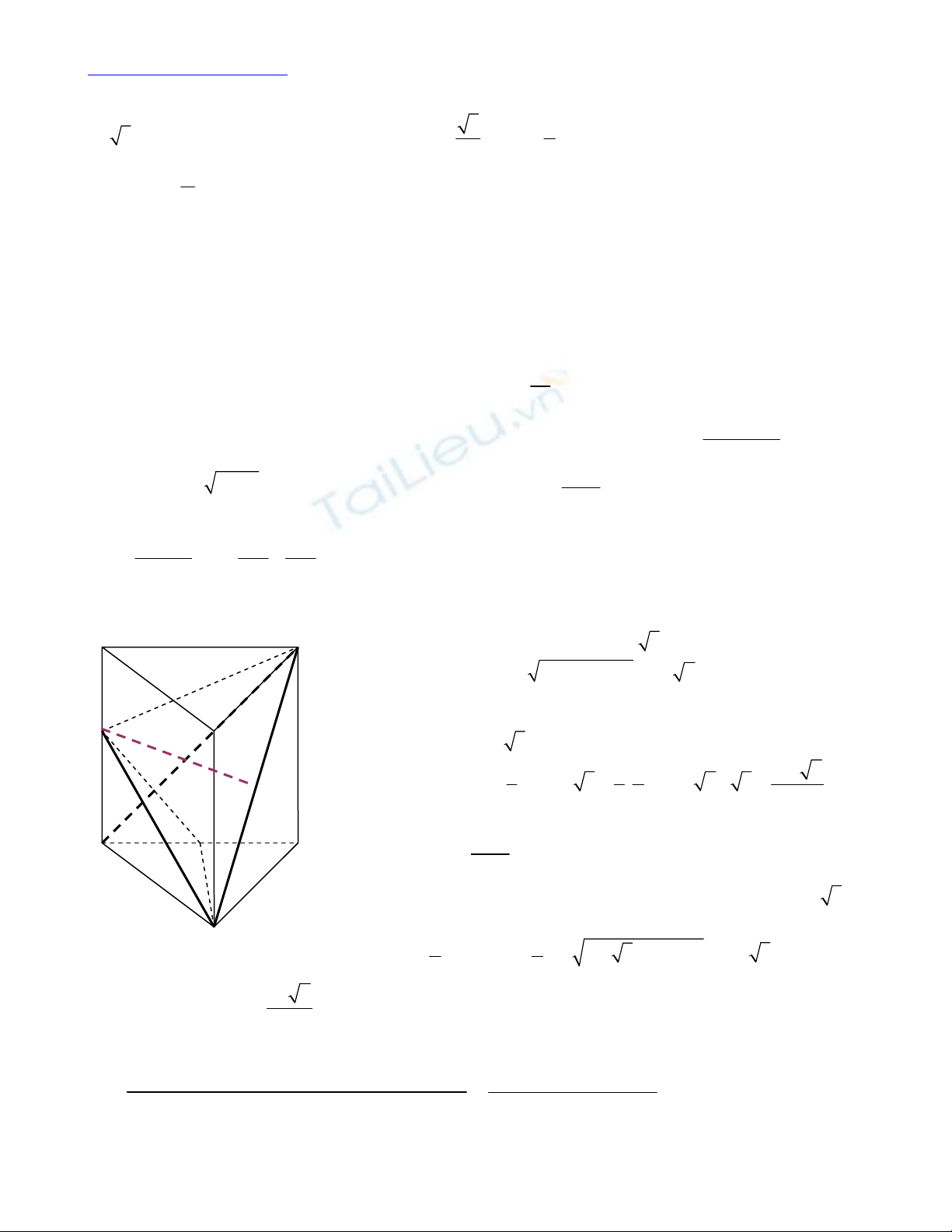
Câu 4 (1 điểm ). Cho lăng trục đều ABC. A’B’C’ có AA’ = 4a 2, cạnh đáy là 2a. M là điểm trên AA’
sao cho BM hợp mặt phẳng ACC’A’ một góc 300.
a) Tính thể tích khối chóp MABC’.
b) Tình khoảng cách từ A đến mặt phẳng (MBC’)
Câu 5 (1 điểm ). Cho x , y là các số thực không âm thoả x + y = 4, tìm GTLN và NN của biểu thức T
=
22
2x 2 x
x 2 2
yy
y
++
+
++
Câu 6 (3 điểm ).
1. Trong hệ trục Oxy, cho đường thẳng d : x – y – 3 = 0 và đường tròn (C) : x2 + (y + 4)2 = 25. Tam
giác OAB vuông cân tại O, có A thuộc d và B thuộc (C). Tìm toạ độ điểm A, B.
2. Trong hệ trục Oxyz cho đường thẳng d : x = 2t – 5; y = t ; z = t – 4 và mặt phẳng (P) : x + y – 3z + 6
= 0 . Viết phương trình đường thẳng d’ nằm trong (P) , cắt Oz và vuông góc với d.
3. Tìm m sao cho đường thẳng y = 2x + m cắt đồ thị hàm số y =
2
x 1
x 2
+
+
tại hai điểm A, B sao cho
trung điểm của AB thuộc đường tròn (O; 5).
GIẢI VẮN TẮT.
Câu 1.
2. PT hoành độ giao điểm : x4 – (2m – 1) x2 + 4m – 6 = 0
Δ = 4m2 – 4m + 1 – 16m + 24 = 4m2 – 20m + 25 = (2m – 5)2 ≥ 0.
Với m ≠ 5/2 và , ta có 4 giao điểm , có hoành độ là :
210 3/2
460
mm
m
−>
⎧<=> >
⎨−>
⎩
23;23;2;mm−− −− 2
.
YCBT Ù 0 < 2m – 3 < 4 Ù 3/2 < m < 7/2.
Vậy 3/2 < m < 7/2 , ≠ 5/2.
www.saosangsong.com.vn Năm học 2009-2010 2
Câu 2.
1. 3 sin 4x + cos 4x + cos 2x + cos 2x = 0 Ù 31
sin 4 cos 4 cos 2
22
x
xx+=−
Ù cos(4x - ) cos(2 )
3x
π
π
=+
. . .
2. . Hệ Ù
22
222 2
x 2(x - ) 12
(x - y ) + 4(x ) = 80
yy
y
⎧−+ =
⎪
⎨−
⎪
⎩
Đặt u = x2 – y2 ; v = 2(x – y): 22
12 8; 4
4; 8
80
uv uv
uv
uv
+=
=
=
⎧⎧
<=>
⎨⎨
=
=
+= ⎩
⎩
Cách khác: Đặt a = x + y, b = x – y, ta được hệ: 2
2
(2)1
80
4
ba
ab
2
+
=
⎧
⎪
⎨
+=
⎪
⎩
Thế b = 12/(a + 2) từ phương trình đầu vào phương trình sau, ta được : a2 + 4 =
2
80( 2)
144
a+. . .
Câu 3. Đặt t = x 1e+=> t2 = e x + 1 => 2tdt = ex d x => d x = 2
2
1
tdt
t
−
I = 22
2
11
211
(1) 1 1
tdt dt
tt t t
⎛⎞
=−
⎜⎟
−−+
⎝⎠
∫∫ . . .
Câu 4.
Gọi H là trung điểm AC, ta có B H vuông góc (ACC’A’)
A
B
C
A
B’
C’
M
H
K
Ta có : góc BMH = 300 => MH = BH 33a
=
Ö MA = 22
22
M
HAH a−= => M là trung điểm
AA’.
Vì CC’ //AM nên khoảng cách từ C’ đến (ABM) bằng khoảng cách
từC đến (ABM) = a 3 (chiều cao tam giác ABC).
3
111 26
. . 3 . .2 .2 2. 3
332 3
ABM
a
Sa aaa==
Ö V =
b) Khoảng cách d từ A đến (BMC’) là chiều cao của hình chóp
A.BMC’ : d =
'
3
BMC
V
s
Tam giác BMC’ là tam giác cân tại M biết BM = C’M = 2a 3và
BC’ = 6a. Kẻ đường cao MK , ta tính được diện tích tam giác
BMC’là 22
11
.6.(2 3) (3)
22
a a a
:. '.BC MK
=
−=
33a.
Suy ra : d = 22
3
a.
Câu 5. Đặt x + y = S, xy = P. Ta có: S2 – 4P ≥ 0 Ù P ≤ 4 . Vậy 0 ≤ P ≤ 4.
T =
222 2 22
2x y+ 4x + y + 2y +2y x 4 + x + 2 x
x 2(x+ ) 4
y
yy
+
++ =
2
25(2)2
24
PS S P S
SP
+−+
++

www.saosangsong.com.vn Năm học 2009-2010 3
Thay S = 4 : T = 28
12
P
P
−+
+
8
|
=> T nghịch biến => max T = T(0) = 22/3 , minT = T(4) = 80/16 = 5.
Câu 6.
1. Gọi A(a; a – 3) là toạ độ của A. Vì .0
|||
OA OB
OA OB
⎧=
⎪
⎨=
⎪
⎩
J
JJG JJJG
J
JJGJJJGnên B = (a – 3 ; - a) hay B = (- a + 3; a) .
B thuộc (C) Ù Ù
22
22
( 3) ( 4) 25
( 3) ( 4) 25
aa
aa
⎡−+−+ =
⎢−++ =
⎣
2
2
2140 {0; 1; 7}
220
aa a
aa
⎡−=
<=> ∈ −
⎢+=
⎣
Ghi nhớ: Nếu và là hai vectơ có độ dài bằng nhau và vuông góc nhau, thế thì nếu
u
G
v
G
(; )uAB=
G
thì
(; )
(;)
B
A
v
B
A
−
⎡
=⎢−
⎣
G
.
2. d’ cắt Oz tại giao điểm của Oz và (P) là (0; 0; 2). D’ vừa vuông góc với () (1; 1 ; 3)
P
n
=
−
JJJG
và
, do đó có VTCP là
(2 ;1;1)
d
u=
JJG
()
[,](4;7;1
Pd
nu )
=
−−
JJJG JJG
. Suy ra phương trình của d’ là : 2
47 1
xyz
−
==
−
−
3. Phương trình hoành độ giao điểm : x2 + 1 = (x + 2)(2 x + m) Ù x 2 + (4 + m) x + 2m – 1 = 0
Δ = m2 + 20 > 0 => luôn có 2 giao điểm.
Toạ độ trung điểm I của AB : x = - (m + 4)/2 ; y = - m – 4 + m = - 4
Ta có : (m + 4)2 /4 + 16 = 25 Ù (m + 4)2 = 36 Ù m = 2 hay m = - 10















![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




