MỤC LỤC
Chương1. Ứng dụng của đạo hàm 1
§1 – Đơn điệu của hàm số chứa trị tuyệt đối và lượng giác 1
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
§2 – Xét tính đơn điệu của hàm hợp phần 1 4
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
§3 – Xét tính đơn điệu của hàm hợp phần 2 13
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
§4 – Xét tính đơn điệu của hàm hợp phần 3 26
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
§5 – Ứng dụng đồng biến ngịch biến 39
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
§6 – Cực trị hàm số 46
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
§7 – Cực trị hàm trị tuyệt đối 49
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
§8 – Số điểm cực trị của hàm số tổng và hàm số hợp 70
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
§9 – Giá trị lớn nhất, giá trị nhỏ nhất 93
Bảng đáp án. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
§10 – GTLN - GTNN của hàm số chứa dấu giá trị tuyệt đối (phần 2) 99
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
§11 – Giá trị lớn nhất, giá trị nhỏ nhất (phần 3) 101
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
§12 – Các vấn đề nâng cao khác về GTLN và GTNN của hàm số 104
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
§13 – Tiệm cận 104
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
191 i/191 pTh.S Phạm Hùng Hải – Ô0905.958.921
MỤC LỤC Giáo Viên Phạm Hùng Hải Chuyên Toán 10 - 11 - 12 & LTĐH
ii
§14 – Tiệm cận - VDC 116
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
§15 – Giao điểm của 2 đường cong có yếu tố hình học - lượng giác 119
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
§16 – Biện luận số nghiệm của phương trình dựa vào bảng biến thiên phần 1 122
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
§17 – Biện luận số nghiệm của phương trình dựa vào bảng biến thiên phần 2 139
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152
§18 – Biện luận số nghiệm của phương trình dựa vào bảng biến thiên phần 3 152
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
§19 – Biện luận số nghiệm của phương trình dựa vào bảng biến thiên phần 4 164
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
§20 – Biện luận số nghiệm của phương trình dựa vào bảng biến thiên phần 5 176
Bảng đáp án . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
191 ii/191 pTh.S Phạm Hùng Hải – Ô0905.958.921
Giải chi tiết trên kênh Youtube: Vietjack Toán Lý hóa
(Bạn vào Youtube -> Tìm kiếm cụm từ: Vietjack Toán Lý Hóa -> ra kết quả tìm kiếm)
Hoặc bạn copy trực tiếp Link kênh : https://www.youtube.com/channel/UCGo1lPIGoGvMUHK7m4TwL3A
ỨNG DỤNG CỦA ĐẠO HÀM
1
C
h
ư
ơ
n
g
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
ỨNG DỤNG CỦA ĐẠO HÀM
BÀI 1. ĐƠN ĐIỆU CỦA HÀM SỐ CHỨA TRỊ TUYỆT ĐỐI
VÀ LƯỢNG GIÁC
Câu 1. Có bao nhiêu giá trị nguyên dương của tham số mđể hàm số y=|x3−3x2+m|đồng biến
trên khoảng (1; 2) ?
A2.BVô số. C3.D1.
Câu 2. Có bao nhiêu số nguyên mđể hàm số y=|mx3−mx2+ 16x−32|nghịch biến trên khoảng
(1; 2).
A3.B2.C4.D5.
Câu 3. Có bao nhiêu số nguyên mđế hàm số y=|x−m|+|x+m+ 2|đồng biến trên khoảng
(0; +∞).
A3.B1.C4.DVô số.
Câu 4. Có bao nhiêu số nguyên mđế hàm số y=|x−m|+|x+m+ 2|nghịch biến trên khoảng
(−∞;−3).
A3.B5.C4.DVô số.
Câu 5. Có bao nhiêu số nguyên m∈(−20; 20) để hàm số y=
1
3x3−x2+ (m2+ 2) x+m·cos x
đồng biến trên khoảng (0; π)?
A33.B32.C19.D20.
Câu 6. Có bao nhiêu số nguyên m∈(−20; 20) để hàm số f(x) = |x3−3(m+ 2)x2+ 3m(m+ 4)x|
đồng biến trên khoảng (0; 2)?
A3.B37.C35.D32.
Câu 7. Có tất cả bao nhiêu giá trị nguyên của mđể hàm số y=|x3−mx2+ 12x+ 2m|đồng biến
trên [1; +∞)?
A18.B19.C21.D20.
Câu 8. Có bao nhiêu số nguyên dương mđể hàm số f(x) = |x−m|(x2+ 4x+ 1) đồng biến trên
khoảng (3; +∞)?
A2.B6.C3.D4.
Câu 9. Có bao nhiêu số tự nhiên mđể hàm số f(x) =
sin3x−msin x+ 1
đồng biến trên khoảng
0; π
2?
A1.B3.C2.D0.
191 1/191 pTh.S Phạm Hùng Hải – Ô0905.958.921
1. Đơn điệu của hàm số chứa trị tuyệt đối và lượng giác Giáo Viên Phạm Hùng Hải Chuyên Toán 10 - 11 - 12 & LTĐH
2
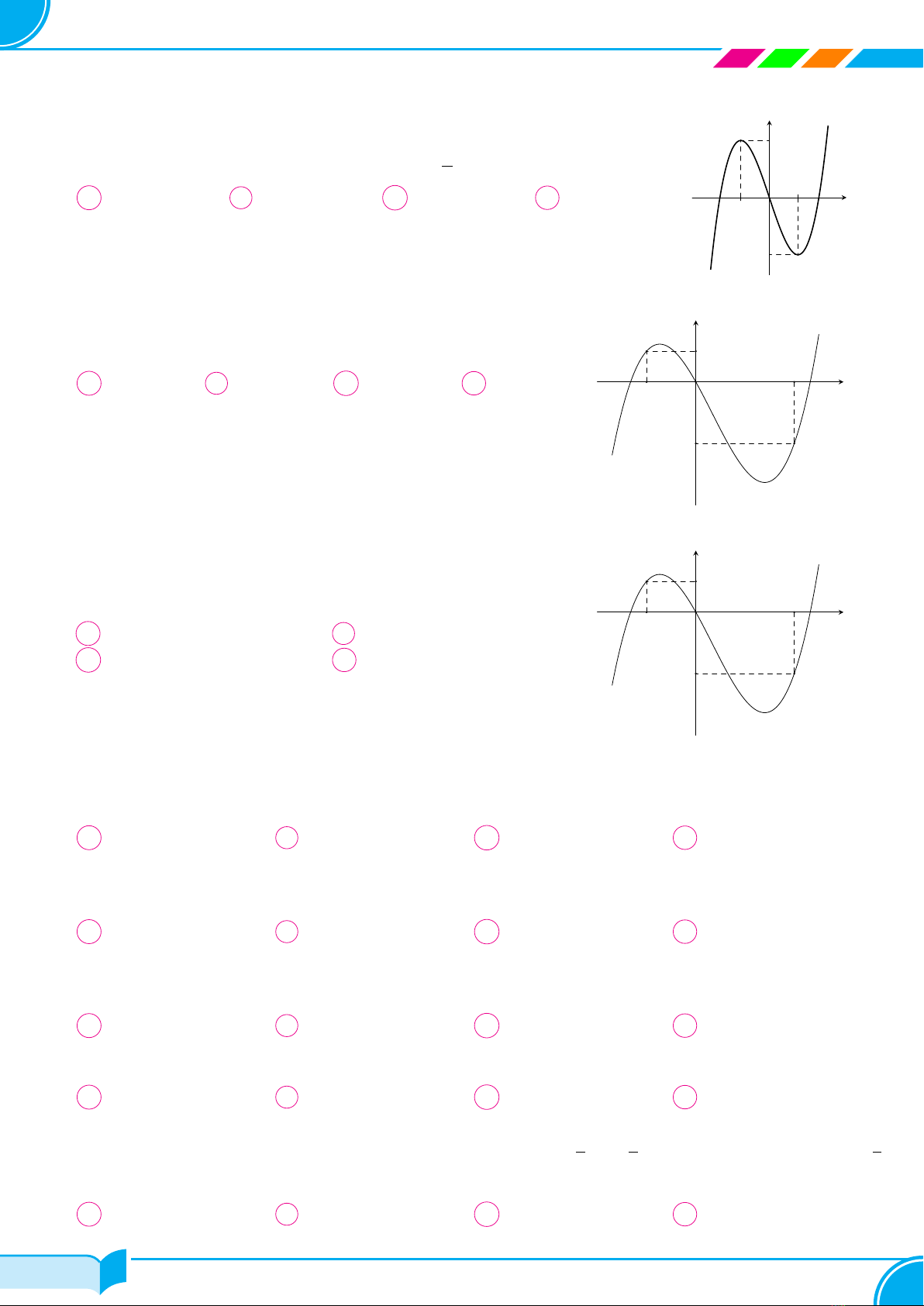
Câu 10. Cho hàm số f(x)có đạo hàm trên Rvà f(1) = 1. Đồ thị hàm
số y=f′(x)như hình bên. Có bao nhiêu số nguyên dương ađế hàm số
y=|4f(sin x) + cos 2x−a|nghịch biến trên 0; π
2?
A2.B3.CVô số. D5.x
y
O
−1
1
Câu 11. Cho hàm số f(x)có đạo hàm trên R. Biết f(0) = 0 và
đồ thị hàm số y=f′(x)như hình bên. Hàm số g(x) = |4f(x) + x2|
đồng biến trên khoảng nào dưới đây?
A(4; +∞).B(0; 4).C(−∞;−2).D(−2; 0).x
y
O
y=f′(x)
4
−2
1
−2
Câu 12. Cho hàm số đa thức f(x)có đồ thị hàm số y=f′(x)như
hình vẽ bên. Điều kiện càn và đủ để hàm số g(x) = |4f(x) + x2−a|
đồng biến trên khoảng (−2; 0) và nghịch biến trên khoảng (0; 4)
là Aa≤4f(−2) + 4.Ba < 4f(4) + 16.
Ca < 4f(−2) + 4.Da≤4f(4) + 16.
x
y
O
y=f′(x)
4
−2
1
−2
Câu 13. Gọi Slà tập hợp tất cả các giá trị nguyên của msao cho hàm số
y=|−x4+mx3+ 2m2x2+m−1|đồng biến trên khoảng (1; +∞). Tổng tất cả các phần tử của S
bằng
A0.B2.C−1.D−2.
Câu 14. Có bao nhiêu giá trị nguyên của asao cho hàm số y=|x3−3x2−ax +a|đồng biến trên
khoảng (0; +∞)?
AVô số. B2.C0.D1.
Câu 15. Có bao nhiêu cặp số nguyên (m;n)với m, n ∈[−5; 5] để hàm số f(x) = |x3−3x2+mx +n|
đồng biến trên (0; +∞)?
A15.B24.C18.D25.
Câu 16. Có bao nhiêu số tự nhiên mđể hàm số y=|x4−mx + 1|đồng biến trên khoảng (1; +∞).
A3.B2.C4.D5.
Câu 17. Có bao nhiêu số nguyên m∈[−9; 9] để hàm số f(x) =
−1
3x3+1
2(2m+ 3)x2−(m2+ 3m)x+2
3
nghịch biến trên khoảng (1; 2)?
A2.B16.C3.D19.
191 2/191 pTh.S Phạm Hùng Hải – Ô0905.958.921
Chương 1. Ứng dụng của đạo hàm Giáo Viên Phạm Hùng Hải Chuyên Toán 10 - 11 - 12 & LTĐH
3
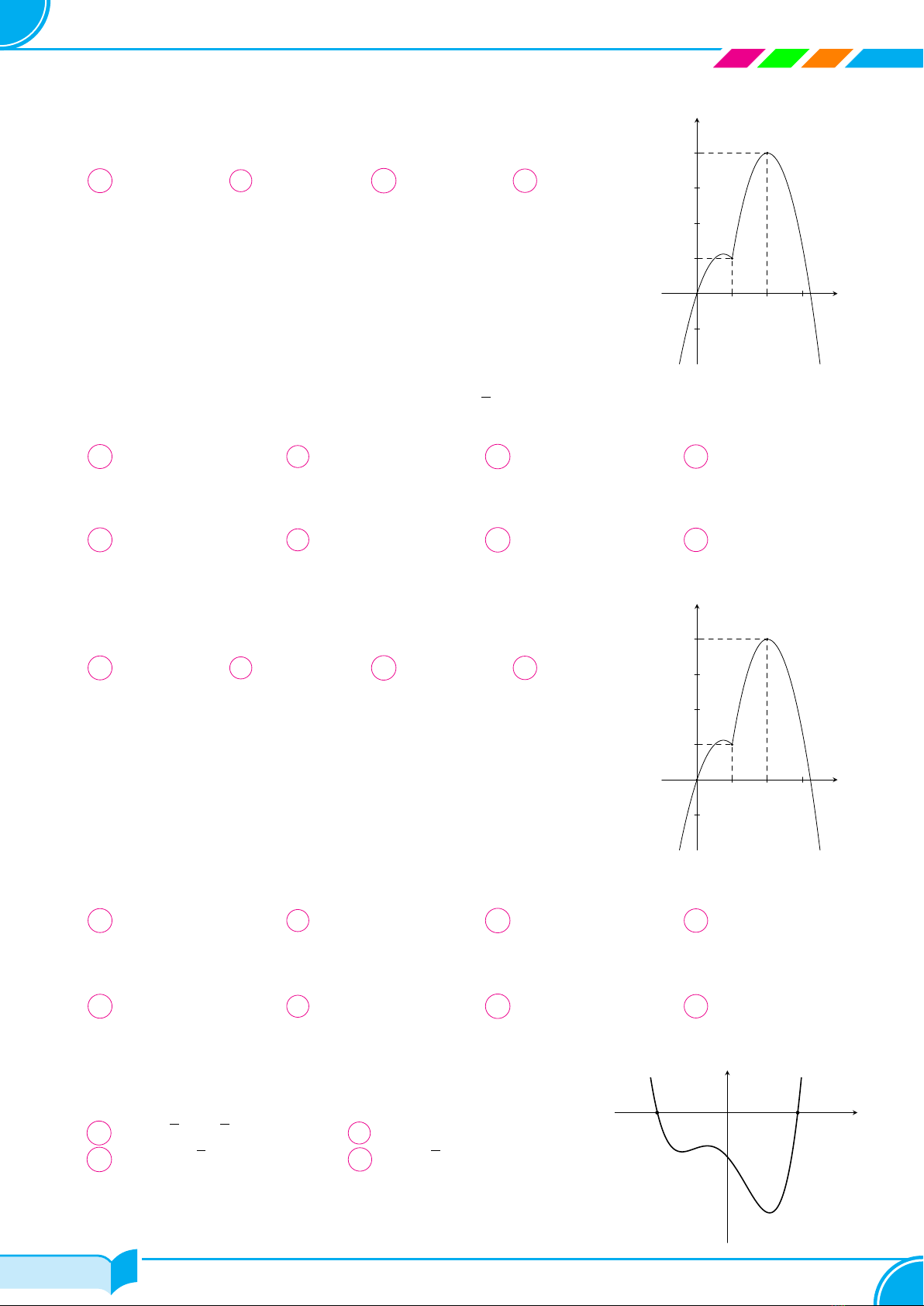
Câu 18. Cho hàm số y=f(x)liên tục trên Rcó f(0) = 0 và đồ thị
hàm số y=f′(x)như hình vẽ bên. Hàm số y=|3f(x)−x3|đồng biến
trên khoảng nào dưới đây?
A(2; +∞).B(−∞; 2).C(0; 2).D(1; 3).
x
y
O1
1
2
4
Câu 19. Có bao nhiêu số nguyên mđể hàm số y=
1
3x3−x2+ (m2+ 5) x+ (3 −m2) cos x+ 1
đồng
biến trên khoảng (0; +∞)?
A3.B5.C7.D4.
Câu 20. Có bao nhiêu cặp số nguyên dương (m;n)với m+n≤16 để hàm số
y=|3x4−mx3+ 6x2+n−3|đồng biến trên khoảng (0; +∞)?
A76.B92.C68.D63.
Câu 21. Cho hàm số f(x)liên tục trên Rcó f(2) = 1 và đồ thị hàm
số f′(x)như hình vẽ bên. Có bao nhiêu số nguyên dương ađể hàm số
y=|3f(x)−x3+a|nghịch biến trên khoảng (0; 2) ?
A3.B5.C6.D4.
x
y
O1
1
2
4
Câu 22. Gọi Slà tập hợp tất cả các giá trị nguyên của msao cho hàm số
y=|x4−mx3−m2x2−m+ 1|đồng biến trên khoảng (1; +∞). Số phần tử của Sbằng
A3.B1.C2.D4.
Câu 23. Có bao nhiêu số nguyên m∈(−20; 20) để hàm số f(x) = (x3−3(m+ 2)x2+ 3m(m+ 4)x)2
đồng biến trên khoảng (0; 2) ?
A3.B37.C35.D32.
Câu 24. Cho hàm số y=f(x)có đồ thị của hàm số y=f′(x)như
hình vẽ bên. Biết f(−2) <0. Hàm số y=|f(1 −x2018)|đồng biến
trên khoảng nào dưới đây?
A(−2018
√3; 2018
√3).B(−1; +∞).
C(−∞;2018
√3).D(−2018
√3; 0).
x
y
O
−2
2
191 3/191 pTh.S Phạm Hùng Hải – Ô0905.958.921