Bài 34
BÀI TẬP VỀ CÁC ĐỊNH LUẬT BẢO TOÀN
I. MỤC TIÊU
- Biết vận dụng các định luật bảo toàn và chuyển hóa năng lượng để giải
một số bài tập từ căn bản đến nâng cao.
II. CHUẨN BỊ
- _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
III. TỔ CHỨC HOẠT ĐỘNG DẠY HỌC
Ổn định lớp học
1) Kiểm tra bài củ :
+ Câu 01 : Va chạm là gì ? Tại sao hệ hai vật va chạm có thể coi là hệ kín
?
+ Câu 02 : Phân biệt va chạm đàn hồi và va chạm mềm ?
+ Câu 03 : Tìm công thức xác định các vận tốc sau va chạm đàn hồi ?
2) Nội dung bài giảng :
Phần làm việc của giáo viên Phần ghi chép của học sinh
Bài 01
GV : Ta xem hệ người – thuyền là hệ
kín (P và FA cân bằng nhau )
Ta gọi :
v : Vận tốc người đối với thuyền.
V : Vận tốc thuyền đối với nước.
GV : Các em cho biết vận tốc người
đối với nước ?
HS : v + V
GV : Em hạy viết định luật bảo toàn
động lượng cho hệ kín cho bài toán
này ?
HS : M(v + V) + MV = 0
GV :
m
M
m
v
V
Chúng ta biết rằng thời gian để
người đi từ đầu đến cuối thuyền cũng
là thời gian để thuyền dịch chuyển
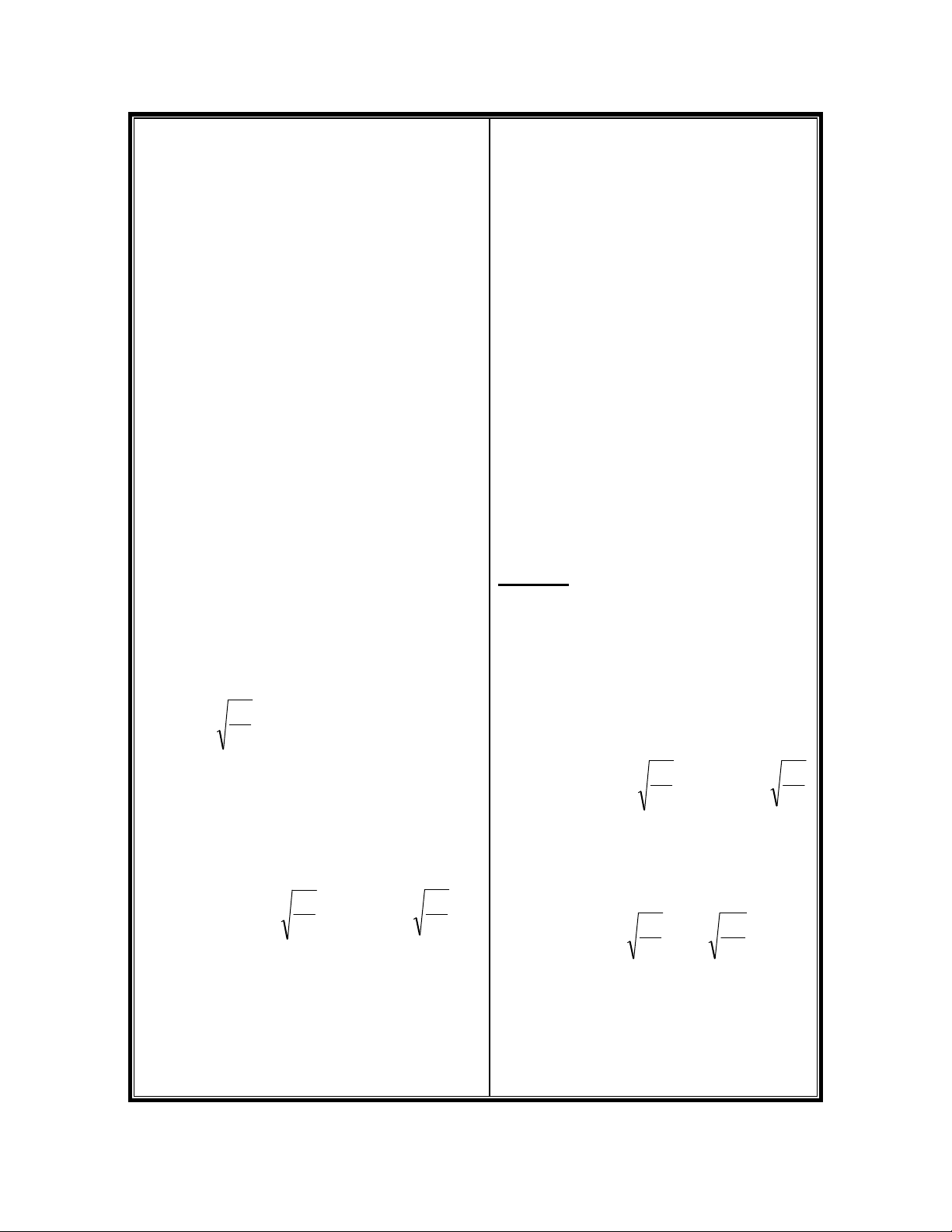
Bài 01 : M
ột chiếc thuyền có
chiều dài L = 5,6 m, khối lư
ợng 80
kg chở một người có khối lư
ợng 52
kg, cả hai ban đầu đứng y
ên trên
mặt hồ phẳng lặng. Nếu ngư
ời
bư
thuyền thì thuy
ền dịch chuyển so
với mặt nước được độ dời bằ
ng
nhiêu và theo chiều nào ? B
ỏ qua
sức cản của nước.
Bài giải
Ta xem hệ người – thuyền là h
ệ
kín (P và FA cân bằng nhau )
Ta gọi :
v : Vận tốc người đối với thuyền.
V : Vận tốc thuyền đối với nước.
v + V : Vận tốc ngư
ời đối với
nước.
Áp dụng định luật bảo toàn đ
ộng
được độ dời s : t =
V
s
v
L
Từ đó ta tìm được :
s =
v
VL = –
m
M
m
. L
s = –
52
80
52
.5,6 = – 2,2 m
GV : các em có nhận xét như thế nào
về dấu “-“ trong trường hợp này ?
HS : Dấu “–“ chứng tỏ thuyền chuyển
động người chiều với người.
Bài 02 :
lượng cho hệ kín :
M(v + V) + MV = 0
m
M
m
v
V
Thời gian để ngư
ời đi từ đầu đến
cuối thuyền cũng là th
ời gian để
thuyền dịch chuyển đư
ợc độ dời s :
t =
V
s
v
L
Từ đó ta tìm được :
s =
v
VL = –
m
M
m
. L
s = –
52
80
52
.5,6 = – 2,2 m
Nhận xét : dấu “–“ ch
ứng tỏ thuyền
chuyển động ngư
ời chiều với
người.
Bài 02 : M
ột quả cầu có khối
lượng M = 300 g nằm ở mép b
àn.
Một viên đạn có khối lư
ợng 10 g
bắn theo ph
ương ngang đúng vào
Câu a)
GV : các em có thể nhắc lại công thức
tính thời gian của một vật ném xiên ?
HS : t = g
h2
GV : Từ đó các em hãy tính quãng
đường vật đi được sau va chạm ?
HS : s = v.t = v. g
h2 hay v = s. h
g
2
GV : Vận tốc của quả cầu và viên đạn
sau va chạm ?
tâm quả cầu, xuy
ên qua nó và rơi
cách mép bàn
ở khoảng cách nằm
ngang s2 = 15 m, còn quả cầu th
ì
rơi cách mép bàn ở khoảng cách s1
= 6m. Biết chiều cao của bàn so v
ới
mặt đất là h = 1m. Tìm :
a) Vận tốc ban đầu của vi
ên
đạn ?
b) Độ biến thiên đ
ộng năng của
hệ trong va chạm ?
Bài giải
a) Áp d
ụng công thức chuyển động
của vật đư
ợc ném ngang từ một độ
cao h so với mặt đất ta có :
s = v.t = v. g
h2 hay v = s. h
g
2
Vận tốc của quả cầu sau va chạm :
v1 = s1. h
g
2= 6. 1.2
8,9
= 13,3
m/s
Vận tốc đạn sau va chạm :
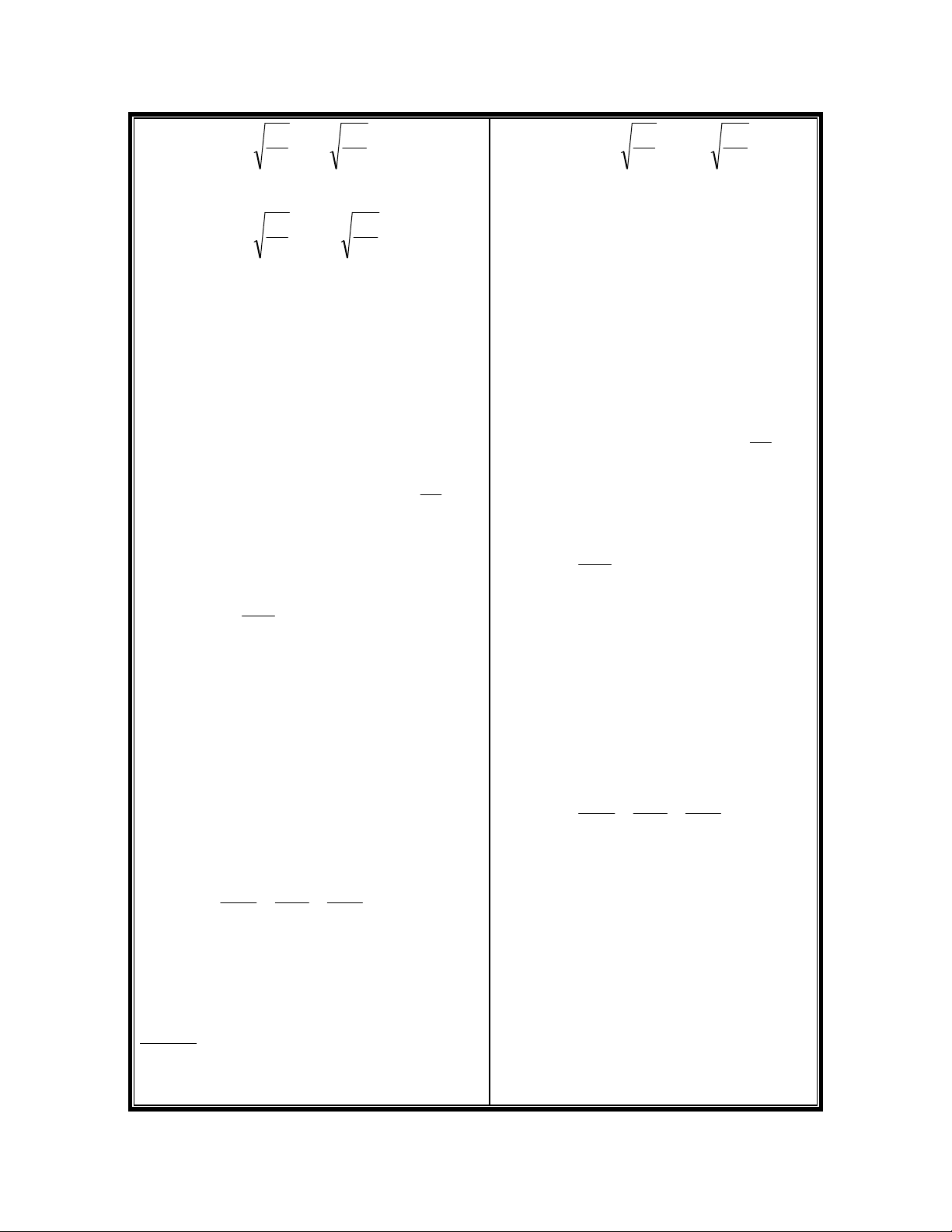
v1 = s1. h
g
2= 6. 1.2
8,9 = 13,3 m/s
v2 = s2. h
g
2= 15. 1.2
8,9 = 33,2 m/s
GV : Gọi u là vận tốc ban đầu của đạn,
các em hãy áp dụng định luật bảo toàn
động lượng theo phương ngang cho hệ
đạn và quả cầu !
HS : m.u = M.v1 + mv2 u =
m
Mv1 +
v2
= 01,0
3,0 13,3 + 33,2 = 432 m/s
b) GV : Em hãy tính độ biến thiên
động năng của hệ trong quá trình va
chạm ?
HS : Wđ = Wđ2 – Wđ1
=
2
2
2
2
2
2
2
1mu
mvMv
= 26,5 + 5,5 – 933 = - 901 (J)
Bài 03 :
v2 = s2. h
g
2= 15. 1.2
8,9
= 33,2
m/s
Gọi u là v
ận tốc ban đầu của đạn,
áp dụng định luật bảo toàn đ
ộng
lượng theo phương ngang cho h
ệ
đạn và quả cầu, ta có :
m.u = M.v1 + mv2 u =
m
Mv1
+
v2
= 01,0
3,0 13,3 + 33,2 = 432 m/s
b) Ta tính biến thiên đ
ộng năng của
hệ trong quá trình va chạm :
Wđ = Wđ2 – Wđ1
=
2
2
2
2
2
2
2
1mu
mvMv
= 26,5 + 5,5 – 933 = - 901
(J)
Như v
ậy : Độ giảm động năng
chuyển thành nhiệt lư
ợng tỏa ra sau
khi va chạm.