Bài tập về Diện tích hình phẳng (Phần 2)

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:4

Thêm vào BST

Báo xấu

22
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài tập về Diện tích hình phẳng (Phần 2) cung cấp cho các bạn những dạng bài toán thuộc chủ đề Diện tích hình phẳng như: hàm số bậc bốn; hàm số bậc ba; diện tích hình phẳng giới hạn; đồ thị hàm số. Mời các bạn tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài tập về Diện tích hình phẳng (Phần 2)

– Câu 1: Hàm số bậc ba y  f  x  có đồ thị  C1  đi qua điểm A 1;0  ; hàm số bậc hai y  g  x  có đồ thị  C2  đi qua điểm B 1; 4 .  C1  ,  C2  cắt nhau tại ba điểm phân biệt có hoành độ lần lượt là 1; 2;3 . Tính diện tích hình phẳng giới hạn bởi hai đồ thị  C1  ,  C2  115 32 71 112 A. B. C. D. 3 3 6 3 Câu 2: Biết đồ thị  C  của hàm số f  x   x  bx  c  b, c    có điểm cực trị là A 1; 0  . Gọi  P  là 4 2 parabol có đỉnh I  0; 1 và đi qua điểm B  2;3 . Diện tích hình phẳng giới hạn bởi  C  và  P  thuộc khoảng nào sau đây? A.  0;1 B.  2;3 C.  3; 4  D. 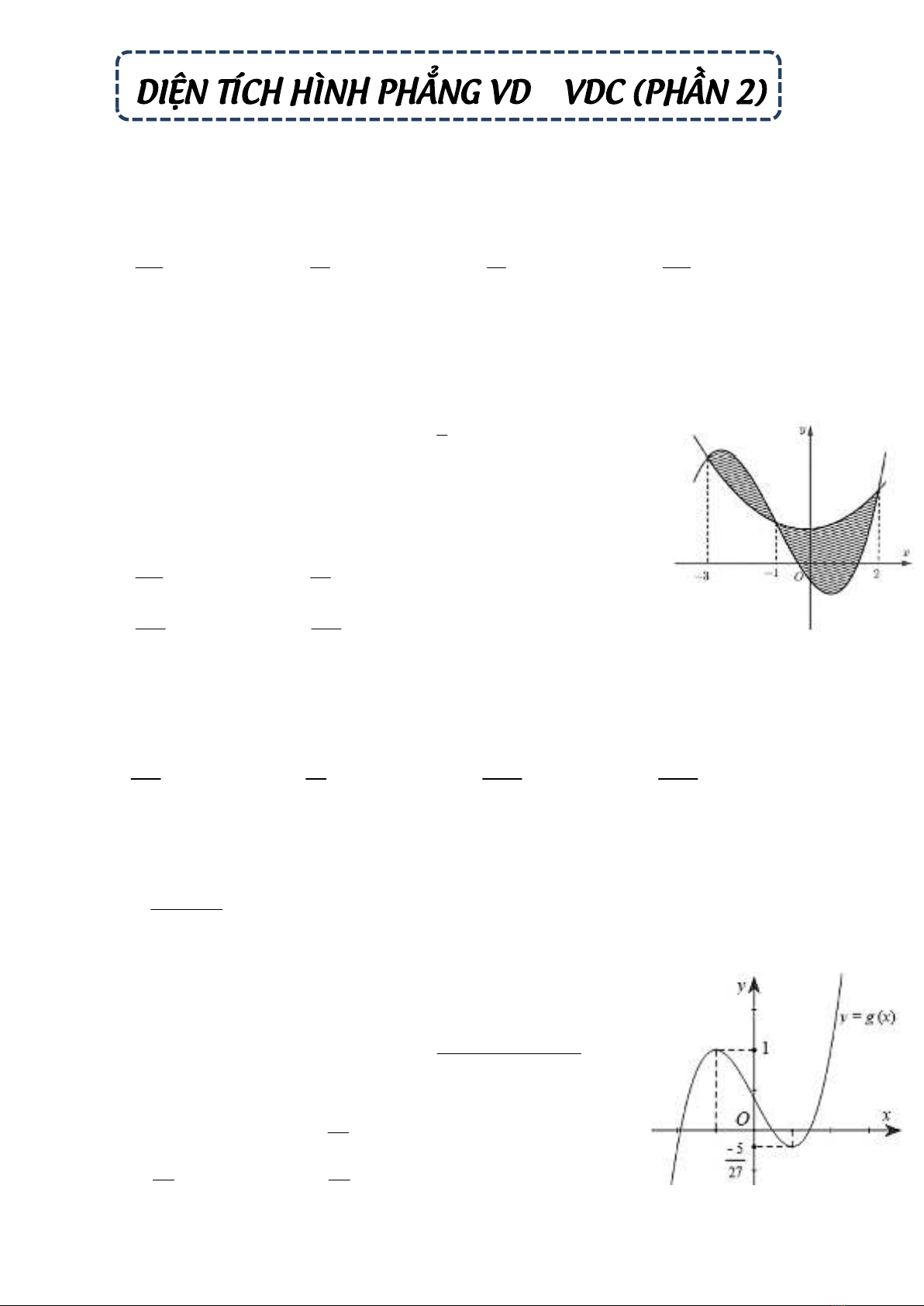1; 2  1 Câu 3: Cho hai hàm số y  f  x   ax3  bx2  cx  và y  g  x   dx 2  ex  1 2 trong đó a, b, c, d , e là những số thực. Biết rằng hai đồ thị đó cắt nhau tại các điểm có hoành độ lần lượt bằng 3; 1; 2 (tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đường y  f  x  và y  g  x  bằng 125 63 A. B. 48 16 253 253 C. D. 48 24 Câu 4: Cho hàm số f  x   3x 4  ax3  bx 2  cx  d a, b, c, d    có ba điểm cực trị là 2 , 1 và 1. Gọi y  g  x  là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y  f  x  . Diện tích hình phẳng giới hạn bởi hai đường y  f  x  và y  g  x  bằng 500 36 2932 2948 A. B. C. D. 81 5 405 405 Câu 5: Cho hàm số f ( x)  2x3  ax2  bx  c với a, b, c là các số thực . Biết hàm số g ( x)  f ( x)  f '( x)  f ''( x) có hai giá trị cực trị là 6 và 10 . Tính diện tích hình phẳng giới hạn bởi các 2 f ( x)  8 đường y  và y  2 g ( x)  8 A. 2ln 3 B. 4ln 3 C. 3ln 2 D. ln 2 Câu 6: Cho hàm số y  f ( x)  ax  bx  c với a, b, c là các số thực. 2 Biết hàm số g  x  x3  f  x  f '  x  f ''  x có đồ thị như hình vẽ bên. f  x   x3  3x 2  1 Diện tích hình phẳng giới hạn bởi các đường y  g  x  1 và y  1 bằng 22 A. ln 3 B. ln 5 44 27 C. ln D. ln 27 11
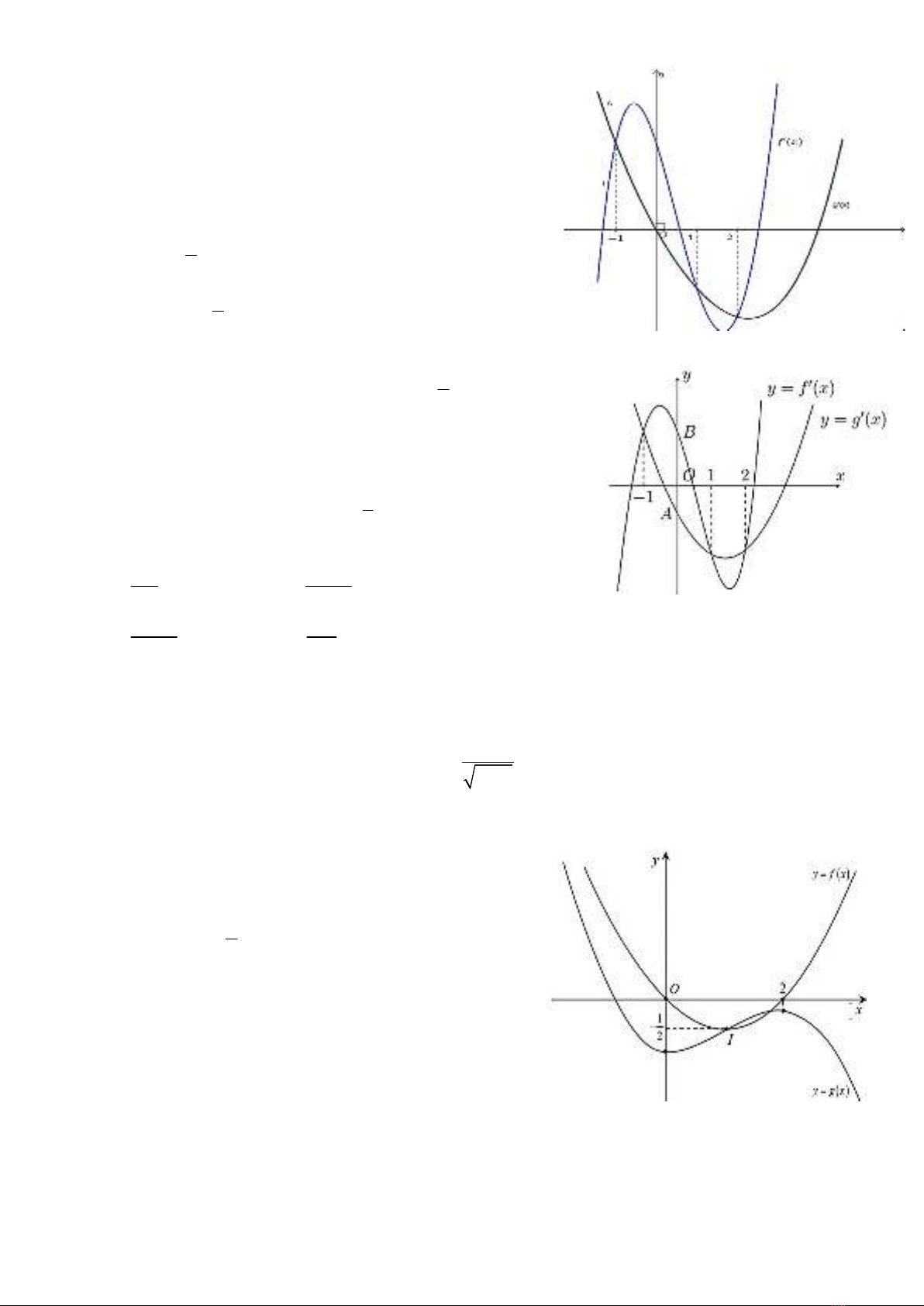
Câu 7: Cho các hàm số f  x   mx4  nx3  px2  qx  r và g  x  ax3  bx2  cx  d  m, n, p, q, r, a, b, c, d  thỏa mãn f  0   g  0  . Các hàm số y  f   x  và y  g   x  có đồ thị như hình vẽ bên. Gọi S là tổng tất cả nghiệm của phương trình f  x   g  x  . Khi đó mệnh đề nào sau đây đúng ?  3  A. S    ; 1 . B. S   0;1 .  2   3 C. S   2;   . D. S  2.  2 4 Câu 8: Cho hàm số f  x   ax 4  bx 3  cx 2  dx   a, b, c, d   3 và g  x   mx3  nx 2  px  m, n, p    .Đồ thị hai hàm số f '  x  và g '  x  được cho ở hình vẽ bên. Tính diện tích hình phẳng giới hạn 1 bởi hai đường y  f  x  và y  g  x    x  2  , biết rằng AB  4 2 3 . 175 14848 A. B. 45 1215 14336 512 C. D. 1215 45 Câu 9: Cho hàm số f ( x)  x 4  bx3  cx 2  dx  e  b, c, d , e    có các giá trị cực trị là 1, 4 và 9. f '( x) Diện tích hình phẳng giới hạn bởi đồ thị hàm g ( x)  và trục hoành bằng f ( x) A. 4 B. 6 C. 2 D. 8 Câu 10: Cho đồ thị hàm số y  f  x  và y  g  x  như hình vẽ bên. Biết đồ thị hàm số của y  f  x  là một Parabol đỉnh 1 I có tung độ bằng  và y  g  x  là một hàm số bậc ba. 2 Hoành độ giao điểm của hai đồ thị là x1 , x2 , x3 thỏa mãn x1.x2 .x3  6. Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số y  f  x  và y  g  x  gần nhất với giá trị nào dưới đây? A. 5. B. 7. C. 6. D. 8.
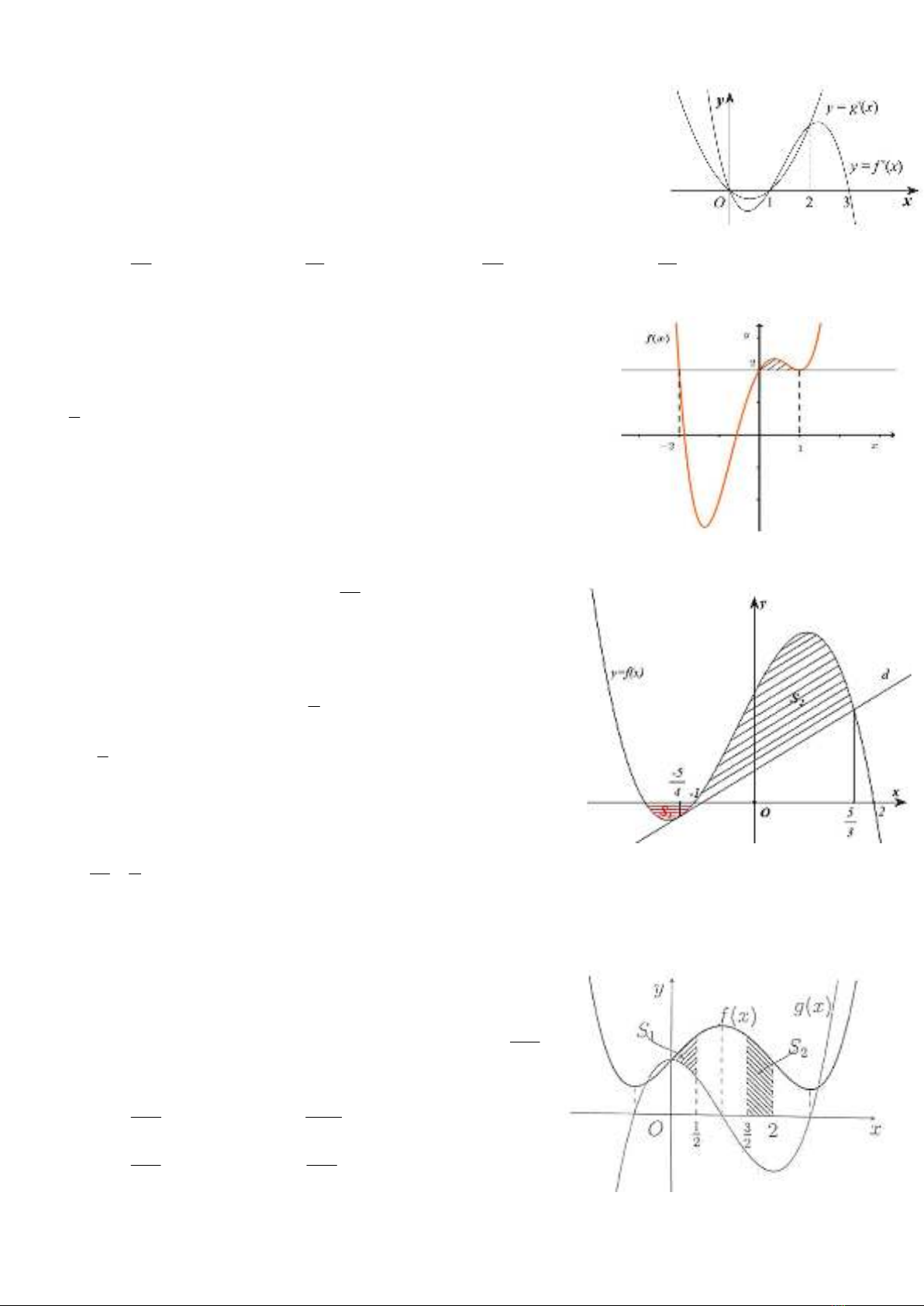
Câu 11: Cho hàm số bậc bốn f  x   ax 4  bx 3  cx 2  dx  e và hàm số bậc ba g  x   mx3  nx 2  px  q . Các hàm số y  f '  x  và y  g '  x  có đồ thị như hình vẽ bên. Biết f 1  g 1  2 và diện tích hình phẳng giới hạn bởi các đồ thị hàm số y  f '  x  , y  g '  x  bằng 4. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y  f  x  , y  g  x  bằng 32 16 16 16 A. B. C. D. 15 3 25 15 Câu 12: Cho hàm số f  x   ax 4  bx 2  cx  d ,  a  0  , có đồ thị tiếp xúc và cắt đường thẳng y  2 tại các điểm có hoành độ x  1, x  0, x  2 (hình vẽ bên). Biết diện tích phần gạch chéo bằng 1 ,gọi g  x  là hàm số bậc hai có đồ thị đi qua 3 điểm cực trị của đồ 5 thị hàm số f  x  .Diện tích hình phẳng giới hạn bởi hai đường y  f  x  , y  g  x  gần bằng với giá trị nào nhất A. 6 . B. 3 . C. 4 . D. 5 . 1 3 Câu 13: Cho hàm số bậc ba f  x   x  bx 2  cx  d có đồ thị là 2  C  cắt trục hoành tại 3 điểm phân biệt trong đó 2 điểm có hoành độ lần lượt là x  1, x  2. Đường thẳng d là tiếp tuyến của đồ thị 5  C  tại điểm có hoành độ x cắt đồ thị tại điểm có hoành độ 4 5 x  . Gọi S1 là diện tích hình phẳng giới hạn bởi phần đồ thị  C  3 bên dưới trục hoành với trục hoành, S 2 là diện tích hình phẳng giới hạn bởi đồ thị  C  và tiếp tuyến d (như hình vẽ bên). Biết rằng tỉ S1 a số  (phân số tối giản) khi đó 19a  b bằng S2 b A. 459. B. 435. C. 705. D. 775. Câu 14: Cho hàm số f  x   ax 4  x3  2 x  2 và hàm số g  x   bx 3  cx 2  2 có đồ thị như hình vẽ bên. Gọi S1 ; S2 là 221 diện tích các hình phẳng gạch chéo trong hình vẽ, biết S1  . 640 Khi đó S 2 bằng 791 1361 A. B. 640 640 271 571 C. D. 320 640
BẢNG ĐÁP ÁN 1.C 2.B 3.C 4.D 5.B 6.D 7.C 8.B 9.B 10.C 11.A 12.B 13.A 14.A Câu 1: 00:00 - 03:53 Câu 8: 1:02:19 - 1:18:41 Câu 2: 03:55 - 10:15 Câu 9: 1:18:42 - 1:29:39 Câu 3: 10:16 - 18:03 Câu 10: 1:29:40 - 1:44:44 Câu 4: 18:05 - 31:18 Câu 11: 1:44:45 - 1:55:53 Câu 5: 31:20 - 43:16 Câu 12: 1:55:54 - 2:15:50 Câu 6: 43:18 - 53:36 Câu 13: 2:15:51 - 2:31:59 Câu 7: 53:37 - 1:02:18 Câu 14: 2:32:00 - 2:42:09