14 BÀI TOÁN HÌNH HC PHNG
TRONG  THI HC SINH GII
NM 2000-2010
trang 1
Trong các  thi chn hc sinh gii vòng quc gia hàng nm, bài toán hình hc phng c xem là bài
toán cơ bn, bt buc.  gii chúng, òi hi ngi hc nm vng các kin thc cn bn v hình hc
và nng lc tng hp các kin thc ó. Nhm phc v k thi sp n, tôi xin gii thiu vi các em mt
s bài toán trong các k thi va qua, giúp các em có cái nhìn tng quan v mc  và kin thc òi hi
trong các bài thi.
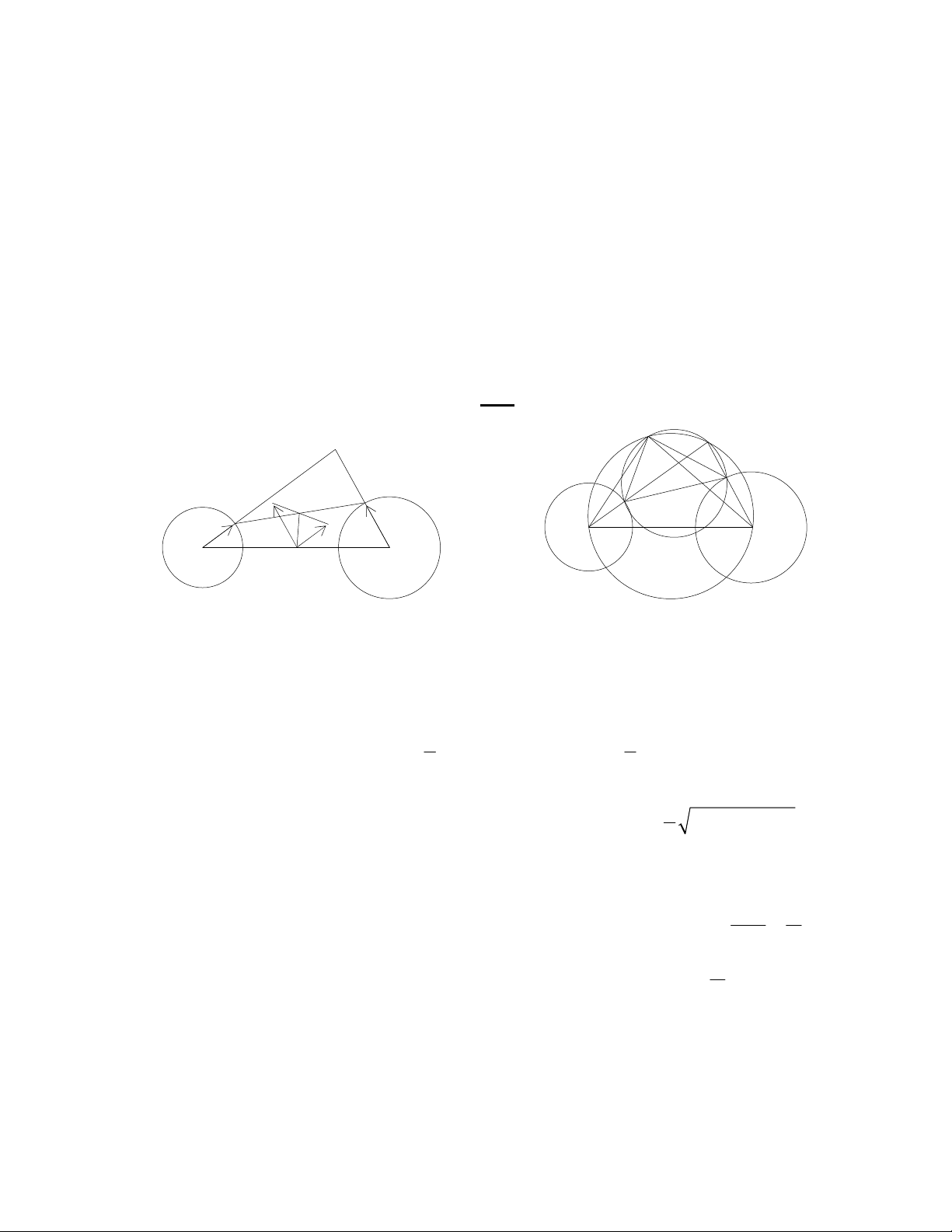
Bài 1. (Bng B - nm 2000)
Trên mt phng cho trc cho hai ng tròn (O1 ; r1) và (O2 ; r2). Trên ng tròn (O1 ; r1) ly
mt im M1 và trên ng tròn (O2 ; r2) ly mt im M2 sao cho ng thng O1M1 ct ng thng
O2M2 ti im Q. Cho M1 chuyn ng trên ng tròn (O1 ; r1), M2 chuyn ng trên ng tròn (O2 ;
r2) cùng theo chiu kim ng h và cùng vi vn tc góc nh nhau.
1) Tìm qu tích trung im on thng M1M2.
2) Chng minh rng giao im th hai ca hai ng tròn ngoi tip tam giác M1QM2 vi ng
tròn ngoi tip tam giác O1QO2 là 1 im c nh.
Gii
1) Gi O là trung im ca O1O2. Hin nhiên O là im c nh.
Ly các im M’1 , M’2 sao cho: 1 1
1 2
1 2
OM' O M , OM' O M
= =
. Vì M1 , M2 tơng ng chuyn ng
trên (O1 ; r1), (O2 ; r2) theo cùng chiu và vi cùng vn tc góc nên M’1 , M’2 s quay quanh O theo
cùng chiu và vi vn tc góc (*).
Ta có : M là trung im M1M2 ⇔ 1 2 1 1 2
2
1 1
OM (OM OM ) OM (O M ' O M ' )
2 2
= + ⇔ = +
⇔ M là trung im ca M’1 , M’2 (**).
T (*), (**) suy ra: qu tích ca M là ng tròn tâm O và bán kính
1 2
1
R 2r 2r d
2
= + −
, trong ó d
= M1M2 = const.
2) Gi P là giao im th hai ca ng tròn ngoi tip tam giác M1QM2 và ng tròn ngoi tip tam
giác O1QO2. D dàng chng minh c: ∆ PO1M1 ng dng ∆ PO2M2. Suy ra
1 1
2 2
PO r
PO r
=
. Do ó, P
thuc ng tròn Apôlôniut dng trên on O1O2 c nh, theo t s không i
1
2
r
r
(1).
D thy 1 2
(PO , PO ) const
= α =
. Suy ra, P thuc cung cha góc nh hng không i α dng trên
on O1O2 c nh (2). T (1), (2) suy ra P là im c nh (pcm).
Q
O1 O2
O
M1’
M2’
M1
M2
M
Q
O1 O2
M1
M2
P
www.VNMATH.com
trang 2
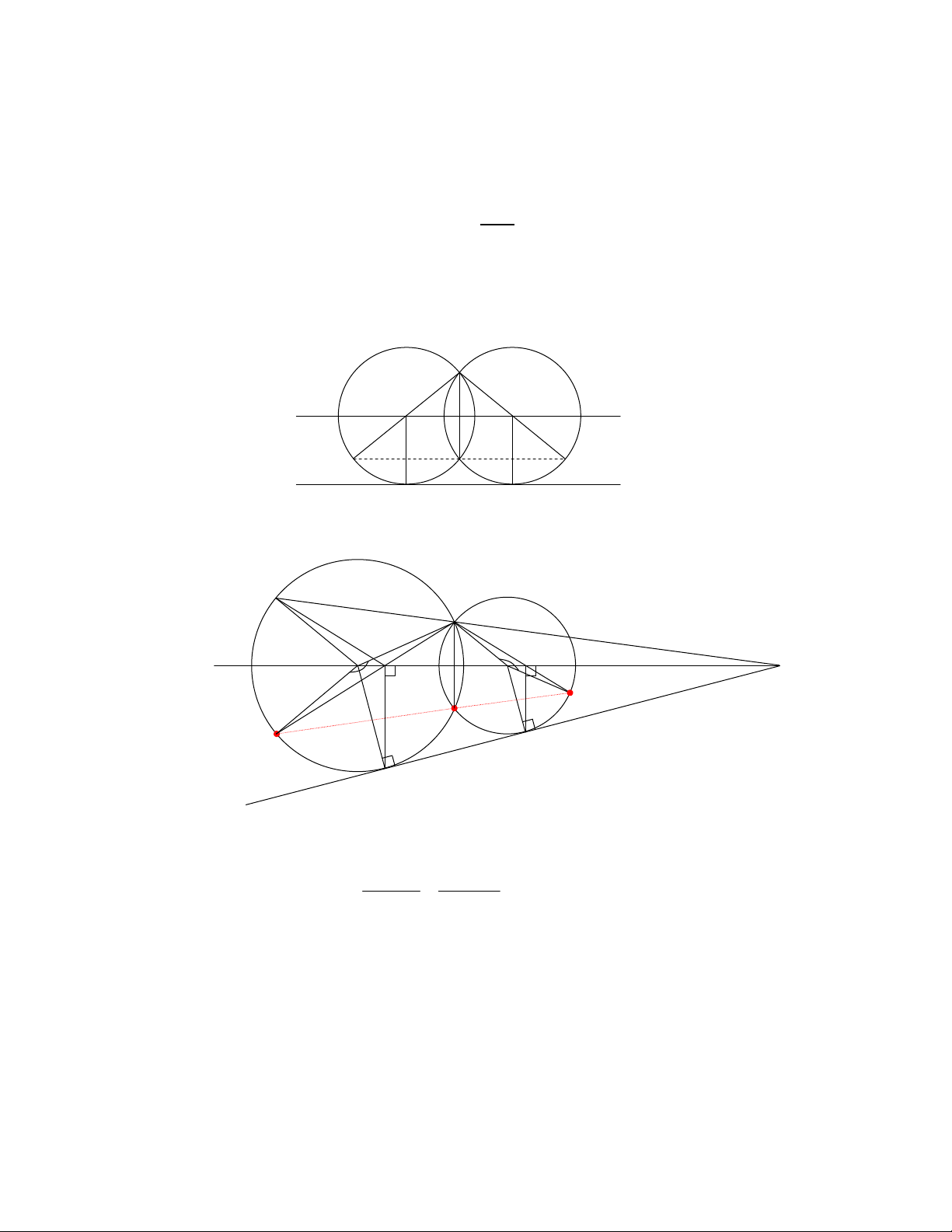
Bài 2. (Bng B - nm 2001)
Trong mt phng cho hai ng tròn (O1) và (O2) ct nhau ti hai im A, B và P1 , P2 là mt tip
tuyn chung ca hai ng tròn ó (P1
∈
(O1), P2
∈
(O2)). Gi Q1 và Q2 tơng ng là hình chiu vuông
góc ca P1 và P2 trên ng thng O1O2 . ng thng AQ1 ct (O1) ti im th hai M1, ng thng
AQ2 ct (O2) ti im th hai M2. Hãy chng minh M1 , B, M2 thng hàng .
Gii
Gi R1 và R2 tơng ng là bán kính ca (O1) và (O2).
1) Trng hp 1 : R1 = R2. Khi ó Q1 ≡ O1 và Q2 ≡ O2
0
1 2
M BA M BA 90
= = M1 , B, M2 thng
hàng .
2) Trng hp 2 : R1 ≠ R2. Gi s! R1 > R2 .
Khi ó Q1 nm trên on O1O2 và Q2 nm trên tia i ca tia O2O1.
Do ó :
01 1 2 2
1 2
M O A M O A
M BA M BA 180
2 2
+ = − + (*) trong ó
0
1 1
M O A 180
<
Gi S = P1P2 ∩ Q1Q2 thì S là tâm ca phép v t VS bin (O1) thành (O2).
Gi A1 là giao im th hai ca SA và (O1).
Ta có VS : A1 → A ; O1 → O2 ; Q1 → Q2 nên
1 1 1 2 2
O A Q O AQ
=
Mà SP1.SQ1 = SA.SA1 (= SP12) A, Q1 , O1 , A1 cùng thuc mt ng tròn
1 1 1 1 1
O A Q O AQ
=.
Suy ra
1 1 2 2
O AQ O AQ
=
1 1 2 2
M O A M O A
=.
T (*)
0
1 2
M BA M BA 180
+ = M1 , B, M2 thng hàng .
P1 P2
O1
≡
Q1 O2
≡
Q2
M1 M2
B
A
P1
P2
O1
O2
M1
M2
B
A
Q2
Q1
A1
S
www.VNMATH.com
trang 3
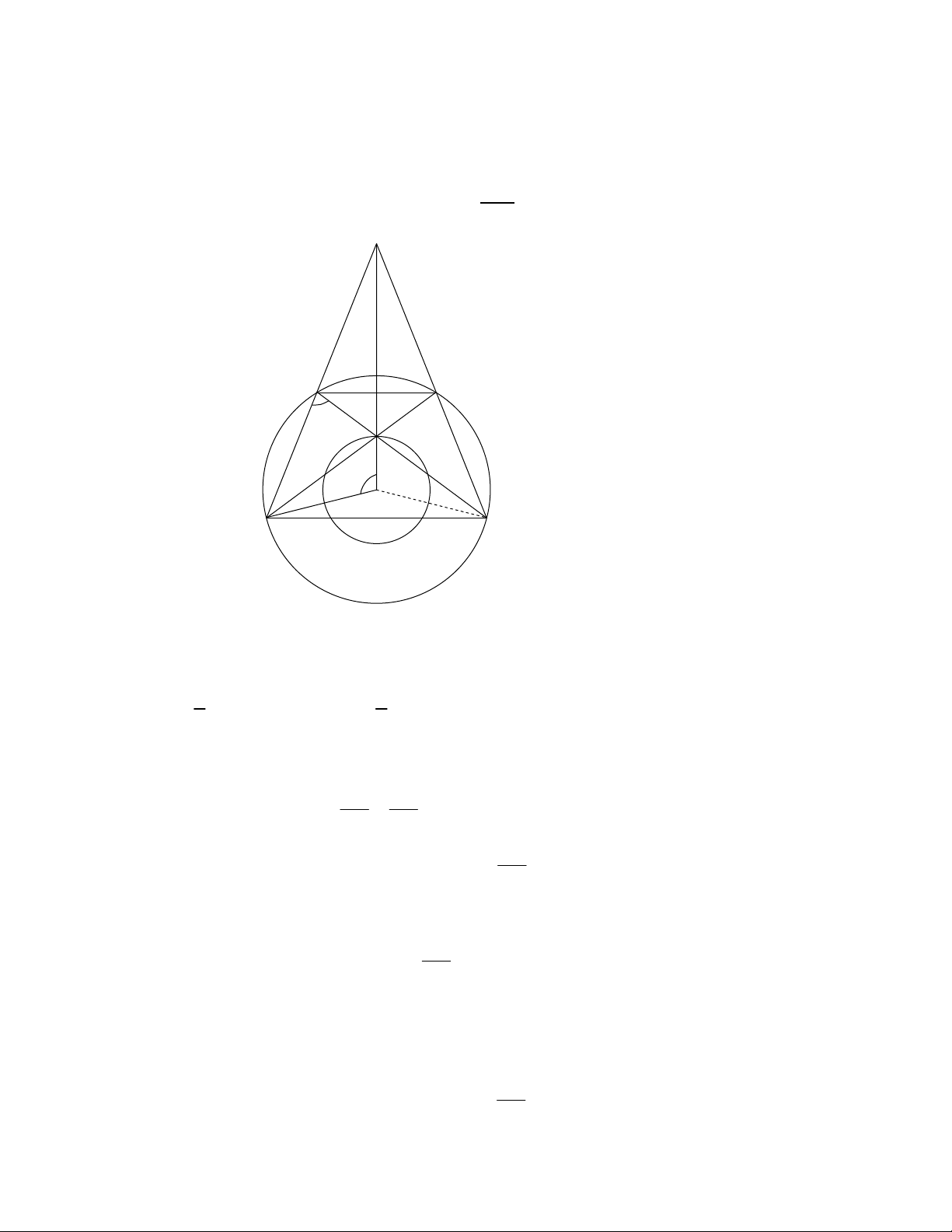
Bài 3. (Bng B - nm 2002)
Trong mt phng cho hai ng tròn c nh (O, R1) và (O, R2) có R1 > R2 . Mt hình thang ABCD
(AB // CD) thay i sao cho bn "nh A, B, C, D nm trên ng tròn (O, R1) và giao im ca hai
ng chéo AC, BD nm trên ng tròn (O, R2). Tìm qu tích giao im P ca hai ng thng AD
và BC .
Gii
1) Phn thun :
Gi I = AC ∩ BD. Vì ABCD là hình thang ni tip nên nó là hình thang cân.
Suy ra OI là tr#c i xng ca hình thang ABCD và O, I, P thng hàng.
Vì
0 0
1 1
POD (DOI IOC) 180 DOC 180 DAC
2 2
= + = − = −
0
POD DAC 180
+ =
t giác AIOD ni tip PA.PD = PI.PO = OP(OP – OI) = OP2 – OP.OI.
Mt khác : PA.PD = P/(O) = OP2 – R12
Suy ra : OP.OI = R12
2 2
1 1
2
R R
OP
OI R
= = = hng s
P chuyn ng trên ng tròn tâm O, bán kính
2
1
2
R
R
.
2) Phn o :
Ly im P bt k$ trên ng tròn (O;
2
1
2
R
R
). Gi I là giao im ca OP và (O, R2). D dàng dng
c hình thang ABCD ni tip ng tròn (O, R1), nhn I làm giao im ca hai ng chéo và và
nhn P là giao im ca hai ng thng cha hai cnh bên.
3) Kt lun :
Tp hp các im P là ng tròn tâm O, bán kính
2
1
2
R
R
.
A B
C
D O
I
P
www.VNMATH.com
trang 4
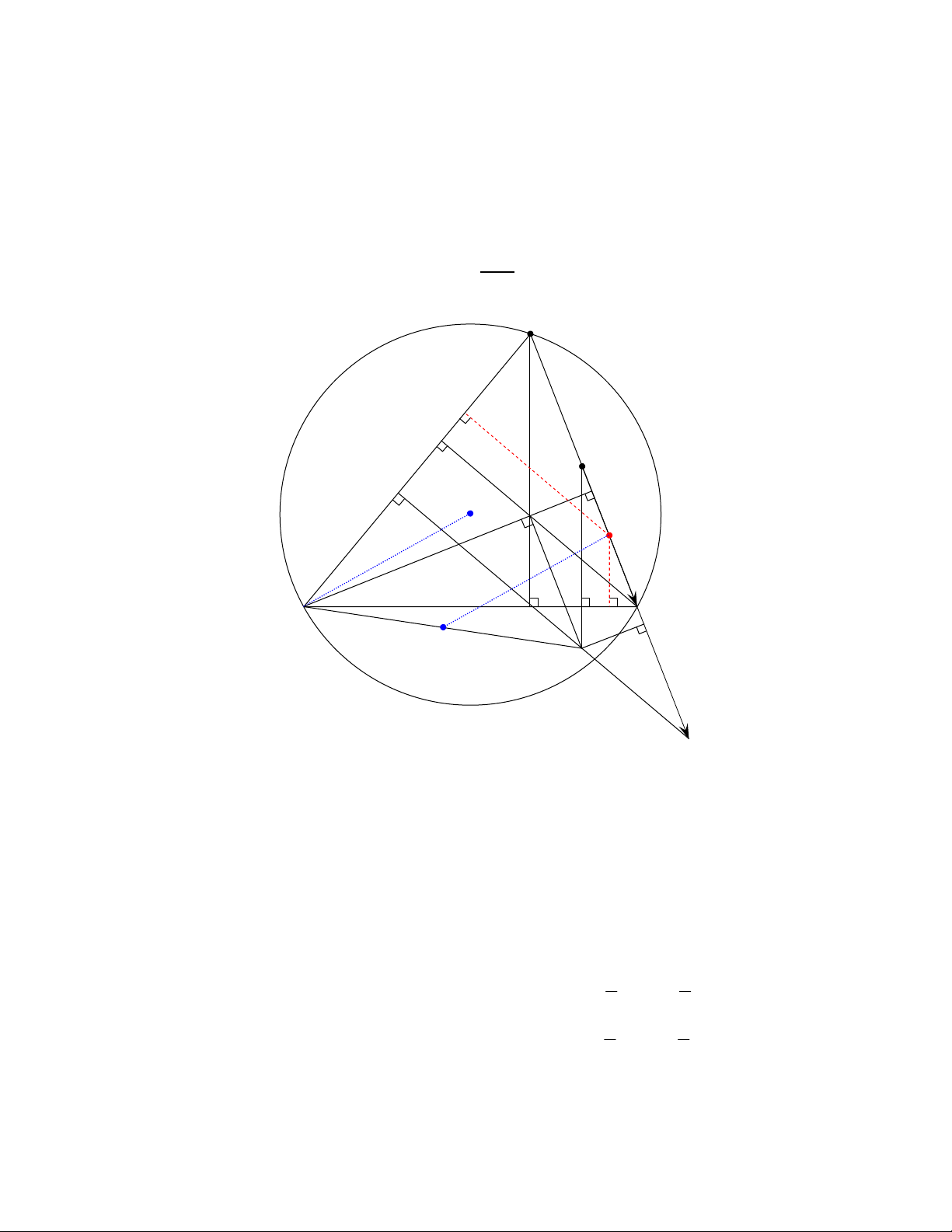
Bài 4. (Bng B - Nm 2003)
Cho tam giác nhn ABC ni tip ng tròn tâm O. Trên ng thng AC ly các im M, N sao
cho
MN AC
=
. Gi D là hình chiu vuông góc ca M trên ng thng BC; E là hình chiu vuông góc
ca N trên ng thng AB.
1) Chng minh rng trc tâm H ca tam giác ABC nm trên ng tròn tâm O’ ngoi tip tam
giác BED.
2) Chng minh rng trung im I ca on thng AN i xng vi B qua trung im ca on
thng OO’.
Gii
1) Gi K = MD ∩ NE.
Vì
0
BEK BDK 90
= = nên ng tròn ng kính BK ngoi tip tam giác BED.
Ta có : AH // MK và CH // NK nên
HAC KMN
= và
ACH MNK
=.
Mt khác AC = MN, suy ra : ∆AHC = ∆MKN. Do ó : d(H, AC) = d(K, AC).
Mà H và K nm cùng phía i vi AC nên KH // AC BH ⊥ KH
H nm trên ng tròn tâm O’, ng kính BK ngoi tip tam giác BED.
2) Gi I1 và I2 l%n lt là hình chiu vuông góc ca I trên AB và BC thì I1 là trung im AE, I2 là trung
im DC. Do ó :
* Hình chiu vuông góc ca
O'I
trên BA và BC l%n lt bng 1
BA
2
và 1
BC
2
* Hình chiu vuông góc ca
BO
trên BA và BC l%n lt bng 1
BA
2
và 1
BC
2
Vy :
O'I BO
=
BO’IO là hình bình hành B và I i xng nhau qua trung im ca OO’.
A
B C
M
N
H
E
D
K
I1
I2
I
O’
O
www.VNMATH.com