BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIAN
THS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84
1
BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIAN
Loại 1. Khoảng cách từ điểm đến mặt phẳng, một đường thẳng
A. Tóm tắt lý thuyết
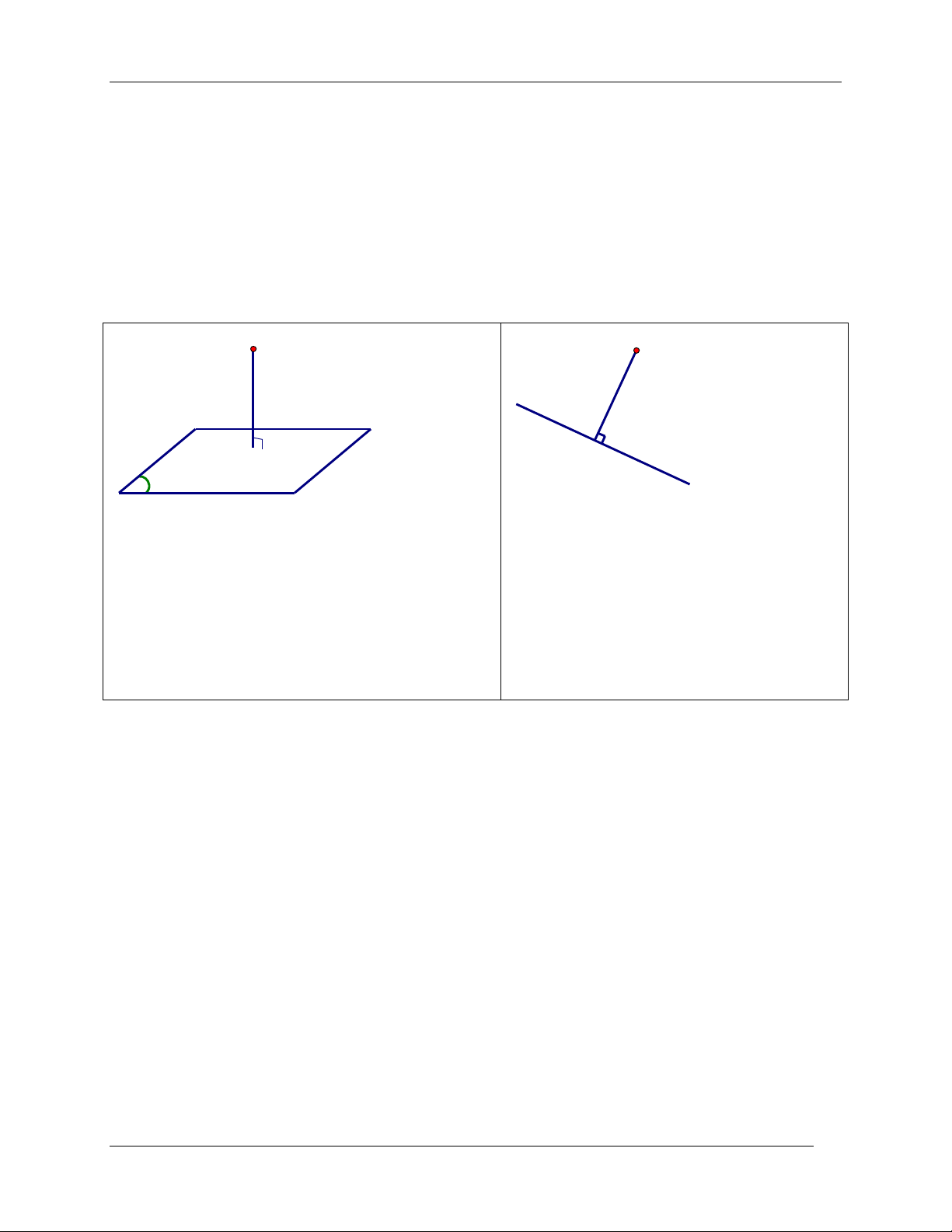
1. Định nghĩa: Khoảng cách từ một điểm đến mặt phẳng (hoặc đường thẳng) bằng khoảng cách
từ điểm đó tới hình chiếu vuông góc của nó lên mặt phẳng (hoặc đường thẳng).
Khoảng cách từ điểm
M
tới mặt phẳng
P
được
ký hiệu là
d M; P
.
là hình chiếu vuông góc của
M
lên
P
thì
d M; P MH
Khoảng cách từ điểm
M
tới đường thẳng
được ký hiệu là
d M;
.
là hình chiếu vuông góc của
M
lên
thì
d M; MH
.
2. Bài toán cơ bản: Nhiều bài toán tính khoảng cách từ điểm tới mặt phẳng, từ điểm tới đường
thẳng có thể quy về bài toán cơ bản sau
Bài toán: Cho hình chóp
S.ABC
có
SA
vuông góc với đáy. Tính khoảng cách từ điểm
đến
mặt phẳng
SBC
và khoảng cách từ điểm
S
đến đường thẳng
BC
.
Cách giải
H
P
M
Δ
M
H
BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIAN
THS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84
2
Gọi
D
là chân đường vuông góc hạ từ
xuống
BC
,
là chân
đường vuông góc hạ từ
xuống
SD
. Ta có
+)
SA ABC
BC SA
, lại có
BC AD
(do dựng)
BC SAD
SD BC
d S;BC SD
.
+) Từ chứng minh trên, đã có
BC SAD
AH BC
, lại
có
AH SD
(do vẽ)
AH SBC
d A; SBC AH
.
3. Một số lưu ý
* Về cách tính khoảng cách một cách gián tiếp
+)
MN P
d M; P d N; P
.
+)
M, N Q
Q P
d M; P d N; P
.
+)
MN P I
d M; P d M; Q
MI NI
.
Trường hợp đặc biệt:
I
là trung điểm của
MN
d M; P d N; P
.
+)
MN
d M; d N;
.
+)
MN I
d M; d M;
MI NI
.
Trường hợp đặc biệt:
I
là trung điểm của
MN
d M; d N;
.
* Về cách sử dụng thể tích để tính khoảng cách từ điểm đến mặt phẳng: Cho hình chóp
1 2 n
S.A A ...A
. Ta có
3V
S.A A ...A
1 2 n
1 2 n SA A ...A
1 2 n
d S, A A ...A
.
* Khoảng cách từ một đường thẳng tới mặt phẳng song song với nó: Cho
P
,
M
là một
điểm bất kỳ trên
. Khi đó
d ; P d M; P
.
* Khoảng cách giữa hai mặt phẳng song song: Cho
P Q
,
M
là một điểm bất kỳ trên
P
. Khi đó
S
A
C
B
D
H
BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIAN
THS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84
3
d P ; Q d M; Q
.
B. Một số ví dụ
Ví dụ 1. [ĐHD03] Cho hai mặt phẳng
P
và
Q
vuông góc với nhau, cắt nhau theo giao
tuyến
. Lấy
A
,
B
thuộc
và đặt
AB a
. Lấy
C
,
D
lần lượt thuộc
P
và
Q
sao cho
AC
,
BD
vuông góc với
và
AC BD a
. Tính khoảng cách từ
A
đến mặt phẳng phẳng
BCD
.
Giải
Ta có
P Q
,
P Q
,
AC P
,
AC
AC Q
BD AC
. Lại có
BD AB
BD ABC
1
.
Gọi
H
là chân đường vuông góc hạ từ
A
xuống
BC
. Vì
ABC
vuông cân tại
A
nên
AH BC
và
2
2 2
a
BC
AH .
Từ
1
suy ra
AH BD
AH BCD
. Do đó
H
là chân đường vuông góc hạ từ
A
lên
BCD
2
2
;a
d A BCD AH .
Ví dụ 2. [ĐHD12] Cho hình hộp đứng
. ' ' ' '
ABCD A B C D
có đáy là hình vuông, tam giác
'
A AC
vuông cân, '
A C a
. Tính khoảng cách từ điểm
A
đến mặt phẳng
'
BCD
theo
a
.
Giải
Q
P
Δ
a
a
aH
AB
C
D
BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIAN
THS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84
4
'
A AC
vuông cân (tại
A
) nên
'
2
' 2
A C
AC AA a
.
ABC
vuông cân (tại
B
) nên
2
AC
AB a
.
Hạ
'
AH A B
(
'
H A B
) .Ta có
' '
BC ABB A
AH BC
, lại có
'
AH A B
(do dựng)
'
AH BCD
.
AH
là đường cao của tam giác vuông
'
ABA
2 2 2 2 2 2
3
1 1 1 1 1
' 2 2
AH AB AA a a a
6
3
a
AH
.Vậy
6
3
; ' a
d A BCD AH AH.
Ví dụ 3. Cho hình chóp .
S ABC
có
3
SA a
và
SA ABC
. Giả sử
2
AB BC a
,
120
ABC
. Tìm khoảng cách từ
A
đến mặt phẳng
SBC
.
Giải
Dựng
AD BC
(
D BC
) và
AH SD
(
H SD
).
Thật vậy, từ giả thiết ta có
CD SA
, lại có
CD AD
(do dựng)
CD SAD
AH CD
, mà
AH SD
AH SCD
H
là chân đường
vuông góc hạ từ
A
lên
SBC
.
Ta có
sin 2 sin 60 3
AD AB ABD a a
.
AH
là đường cao của tam giác
SAD
vuông tại
A
nên:
2 2 2 2 2 2
1 1 1 1 1 4
9 3 9
AH AS AD a a a
3
2
a
AH
. Vậy
3
2
;
a
d A SBC AH
.
a
a 2
a 2
2a
C
C'
D
D
'
A
A
'
B
B
'
H
2a 2a
3a
120o
S
A
C
B
D
H
BÀI GIẢNG ÔN THI VÀO ĐẠI HỌC BÀI TOÁN KHOẢNG CÁCH TRONG HÌNH HỌC KHÔNG GIAN
THS. PHẠM HỒNG PHONG – GV TRƯỜNG ĐH XÂY DỰNG DĐ: 0983070744 website: violet.vn/phphong84
5
Ví dụ 4. [ĐHD11] Cho hình chóp .
S ABC
có đáy là tam giác vuông tại
B
,
3
BA a
,
4
BC a
;
mặt phẳng
SBC
vuông góc với mặt phẳng
ABC
. Biết
2 3
SB a
và
30
SBC
. Tính
khoảng cách từ điểm
B
đến mặt phẳng
SAC
theo
a
.
Giải
Hạ
SK BC
(
K BC
). Vì
SBC ABC
nên
SK ABC
.
Ta có
3
2
cos 2 3. 3
BK SB SBC a a
4 3
KC BC BK a a a
.
Do đó nếu ký hiệu
1
d
,
2
d
lần lượt là các khoảng cách từ
các điểm
B
,
K
tới
SAC
thì 1
2
4
dBC
d KC
, hay
1 2
4
d d
.
Hạ
KD AC
(
D AC
), hạ
KH SD
(
H SD
). Từ
SK ABC
AC SK
, lại có
AC KD
(do dựng)
AC SKD
KH AC
, mà
KH SD
(do dựng)
KH SAC
2
d KH
.
Từ
ADK ABA
suy ra: CK
DK
CA BA
. 3 . 3
5 5
BA CK a a a
CA a
DK
(
2 2
2 2
3 4 5
CA BA BC a a a
).
.sin 3
KS SB SBC a
.
KH
là đường cao của tam giác vuông
SKD
nên:
2 2 2 2 2 2
25 28
1 1 1 1
9 3 9
KH KD KS a a a
3 7
14
a
KH .
Vậy
6 7
1 2
7
; 4 4 a
d B SAC d d KH .
Ví dụ 5. [ĐHB11] Cho lăng trụ
1 1 1 1
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật,
AB a
,
3
AD a
. Hình chiếu vuông góc của điểm
1
A
lên mặt phẳng
ABCD
trùng với giao điểm của
AC
và
BD
. Tính khoảng cách từ điểm
1
B
đến mặt phẳng
1
A BD
theo
a
.
Giải
30°
2a 3
4a
3a
K
S
C
A
B
D
H