lùc c¶n trong dßng s«ng vμ kªnh
cã mÆt c¾t phøc t¹p
TS. trÇn ®×nh nghiªn
Bé m«n Thuû lùc - Thuû v¨n - §H GTVT
Tãm t¾t: B¸o c¸o lý gi¶i sù ®¸nh gi¸ nhiÒu mÆt vÒ lùc c¶n trong s«ng vμ trong kªnh theo
quan niÖm cña hai t¸c gi¶ (Rouse 1965 vμ Ben Chie Yen, 2002). §ã lμ vai trß cña h×nh d¹ng
mÆt c¾t tÝnh kh«ng ®Òu cña líp biªn, dßng kh«ng æn ®Þnh vμ tÝnh chÊt nh¸m cña líp biªn khi
xem xÐt søc c¶n cña dßng ch¶y. Tõ ®ã t¸c gi¶ tr×nh bμy søc c¶n cña dßng s«ng cã mÆt c¾t
phøc t¹p vμ nªu ra nh÷ng vÊn ®Ò cÇn nghiªn cøu tiÕp ®Ó chÝnh x¸c h¬n viÖc tÝnh l−u l−îng mÆt
c¾t theo h×nh th¸i mÆt c¾t.
Summary: This report extends critically reviewed hydroulic resistance in reviers and open
channels by Rouse, 1965 and Ben Chi Yen, 2002. Their study showed the offects of cross -
senctional shape, boundary nonuniformity, flow unstedies and wall roughness in hydraulic
resistance. From that points, authors pointed out a compound rivers and channels resistance,
as well ass the need for further research on the subject for better pridicting dischagre based on
the cross - sectional shape of rivers or channels.
1. Giíi thiÖu
Søc c¶n trong dßng ch¶y hë lµ vÊn ®Ò
®−îc nghiªn cøu ®· l©u vµ cã nhiÒu ®ãng gãp
quan träng gióp gi¶i quyÕt dÔ dµng nhiÒu bµi
to¸n thuû lùc vÒ kªnh hë vµ dßng s«ng ®¹t
hiÖu qu¶ cao. Bµi b¸o nµy chØ bµn thªm vÒ lùc
c¶n vµ hÖ sè søc c¶n cña hai t¸c gi¶ lµ Rouse
(1965) ®· ph©n lo¹i khi sö dông hÖ sè søc c¶n
Weisbach, f vµ Ben Chie Yen (2002).
Theo Rouse hÖ sè søc c¶n lµ hµm cña
06 biÕn:
f = f(Re, ks/R, η, N, Fr, U) (1)
trong ®ã: Re lµ hÖ sè Reynolds; ks/R lµ nh¸m
t−¬ng ®èi; R lµ b¸n kÝnh thuû lùc; ks lµ nh¸m
tuyÖt ®èi; η lµ h×nh d¹ng mÆt c¾t ngang; N lµ
tÝnh kh«ng ®Òu cña dßng ch¶y ë d¹ng mÆt c¾t
vµ mÆt b»ng; Fr lµ hÖ sè Froude; U lµ møc ®é
kh«ng æn ®Þnh.
Theo Rouse th× lùc c¶n gåm 4 thµnh
phÇn: Søc c¶n bÒ mÆt; Søc c¶n h×nh d¹ng;
Søc c¶n sãng do bÒ mÆt n−íc bÞ t¹o sãng,
kh«ng b»ng ph¼ng; Søc c¶n g¾n liÒn víi gia
tèc côc bé hay sù kh«ng æn ®Þnh cña dßng
ch¶y. Tõ gãc ®é nµy ta thÊy to¸n ®å cña
Moody dïng tÝnh ®−êng èng lµ mét tr−êng hîp
®Æc biÖt cña (1) ®èi víi dßng ch¶y æn ®Þnh
trong èng cã ®−êng kÝnh kh«ng ®æi, trong ®ã
chØ sö dông hai trong s¸u biÕn lµ sè Re vµ
nh¸m mÆt t−¬ng ®èi ks/R theo Nikurade.
Trong kªnh hë vµ s«ng (gäi chung lµ kªnh hë)
vÊn ®Ò hÖ sè søc c¶n th−êng quan hÖ víi vËn
tèc th«ng qua c¸c c«ng thøc:
C«ng thøc Sªdi: RSCV = (2)
C«ng thøc Maning: 2
1
3
2SR
n
1
V= (3)
C«ng thøc Darcy - Weisbach:
RSf/g8V = (4)
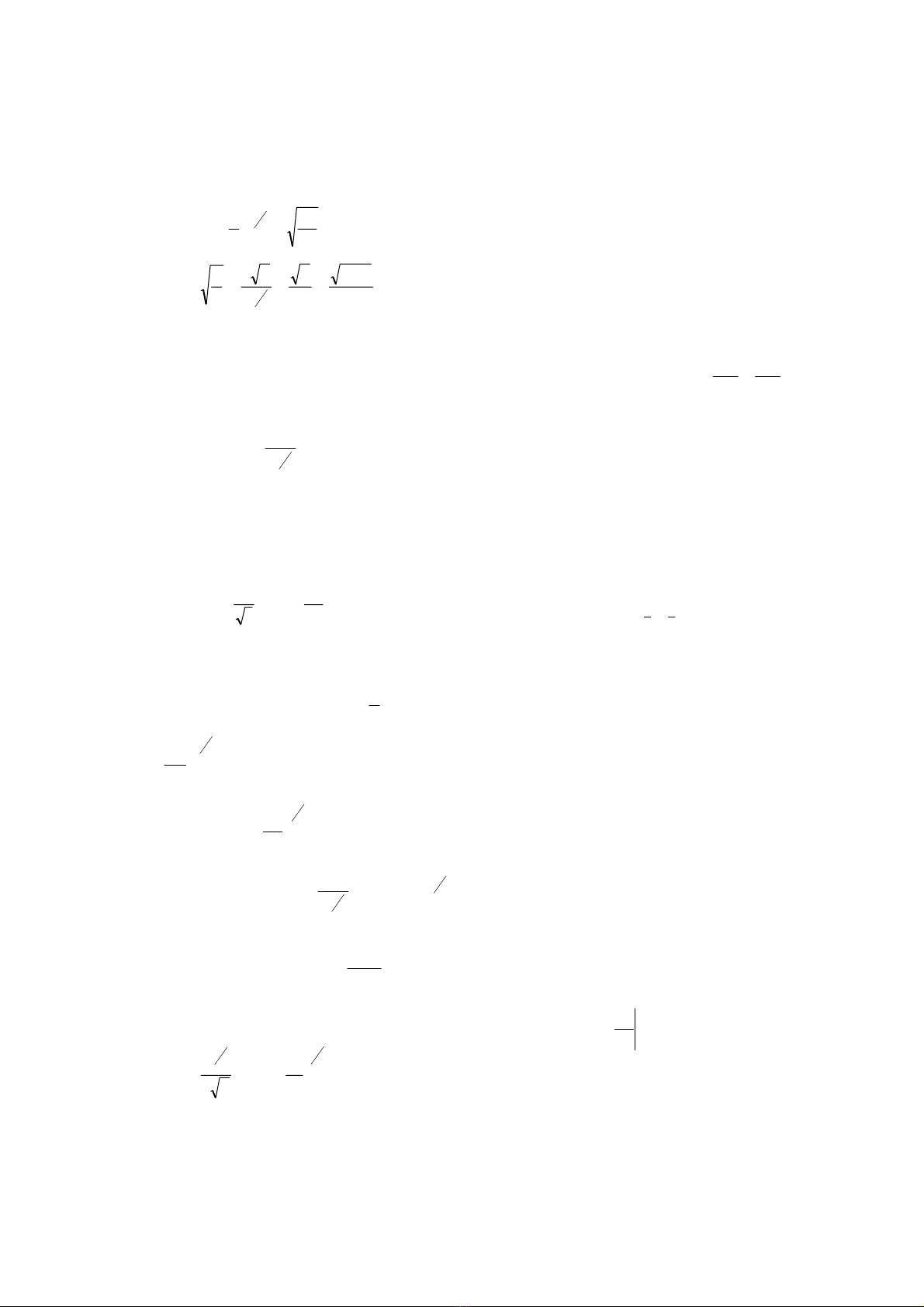
Tõ (2) vµ (4) rót ra hÖ sè søc c¶n cã quan
hÖ:
f
g8
R
n
1
C6
1== (5)
V
gRS
C
g
R
gn
8
f
6
1=== (6)
Tõ (5) vµ (6) chØ cÇn biÕt gi¸ trÞ mét lùc
c¶n nµy sÏ tÝnh ra gi¸ trÞ lùc c¶n kh¸c t−¬ng
øng:
Tõ (2) vµ (4) rót ra quan hÖ t×m trùc tiÕp
hÖ sè f: g8
R
n
f
3
1
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
= (7)
Ph−¬ng tr×nh nµy kh«ng chøa tèc ®é V vµ
sè Re, do ®ã cã thÓ so s¸nh víi quan hÖ
nh¸m cña Karman ®èi víi líp biªn nh¸m khi
Re > 105: Theo Karman - Prandtl:
14.1
D
k
lg2
f
1s+−= (8)
NÕu x©y dùng quan hÖ gi÷a f vµ
4R/k
s ë to¹ ®é log - log sÏ ®−îc ®−êng cong
gÇn nh− th¼ng cã ®é dèc ⎟
⎠
⎞
⎜
⎝
⎛−3
1, do ®ã
f ~
3
1
s
k
R4 −
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ hay:
f ~ 3
1
s
R
k⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ (9-a)
V× f ë (7) quan hÖ víi
3
1
2
R
n nªn n ~ 6
1
s
k
vµ do ®ã c«ng thøc (3) vµ (4) ®Òu thÓ hiÖn
dßng rèi thµnh nh¸m, tøc lµ 60
uk *s >
ν. So
s¸nh (3) víi quy luËt tèc ®é trung b×nh ®èi víi
thµnh nh¸m, ta cã:
6
1
s
6
1
k
R
16.8
gn
R⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
= (9-b)
2. Søc c¶n mÆt vμ lý thuyÕt líp
biªn
Tõ gãc ®é lý thuyÕt líp biªn nh×n nhËn vÒ
lùc c¶n cho thÊy tèc ®é liªn quan chÆt chÏ víi
lùc c¶n. Stokes (n¨m 1845) chØ ra øng suÊt
tiÕp gi÷a c¸c líp chÊt láng tû lÖ víi nhít ®éng
lùc ph©n tö vµ Gradient tèc ®é. Tr−íc ®ã Saint
- Venant (n¨m 1843) ®Ò nghÞ quan hÖ t−¬ng
tù, song tæng qu¸t h¬n ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
ε=τ
i
j
j
i
ij x
u
x
u
(10). §èi víi chÊt láng ch¶y tÇng th× , cßn
chÊt láng ch¶y rèi th×
μ=ε
ε
gåm c¶ nhít ®éng lùc
ph©n tö vµ nhít rèi. øng suÊt tiÕp t¹i thµnh
r¾n lµm c¶n trë chÊt láng chuyÓn ®éng, t¹o ra
vïng líp biªn chÞu ¶nh h−ëng nhít. §èi víi
thµnh tr¬n, líp biªn lµ dßng tÇng vµ u = u(y),
nÕu sè Rex v−ît qua gi¸ trÞ ph©n giíi th× dßng
ch¶y bÞ chËm l¹i sÏ mÊt æn ®Þnh vµ h×nh thµnh
rèi. §èi víi dßng rèi líp biªn liªn quan tíi tèc
®é trung b×nh thêi gian
()
yuu =. TÝnh rèi lµm
cho tèc ®é gÇn thµnh t¨ng t¹o thµnh h×nh bao
tèc ®é ®Çy ®Æn h¬n so víi dßng tÇng. NÕu bÒ
mÆt lµ nh¸m, líp biªn rèi cã thÓ h×nh thµnh
ngay ë mÐp ®Çu mÆt nh¸m, x©m nhËp th¼ng
tíi thµnh ng¨n c¶n h×nh thµnh líp biªn tÇng.
Ngoµi líp biªn, dßng ch¶y tù do hÇu nh−
kh«ng cã øng suÊt tiÕp vµ tr−êng tèc ®é trung
b×nh coi nh− dßng thÕ, dßng nµy coi nh−
kh«ng rèi so víi rèi cao h¬n rÊt nhiÒu trong
líp biªn. Nghiªn cøu chØ ra kh«ng thÓ dïng
mét ph−¬ng tr×nh duy nhÊt m« t¶ sù thay ®æi
tèc ®é mµ tån t¹i vµi ph−¬ng tr×nh th«ng dông
cho khu vùc s¸t thµnh tr¬n vµ quy luËt thiÕu
hôt tèc ®é ¸p dông cho phÇn trªn cña líp biªn
®èi víi c¶ thµnh tr¬n vµ nh¸m. T¹i thµnh kªnh
øng suÊt tiÕp côc bé 0
τ
lµ:
0y
0dy
du
=
μ=τ (10)
trong ®ã y cã chiÒu vu«ng gãc víi thµnh, cßn
u lµ vÐct¬ tèc ®é, nh×n chung chÞu ¶nh h−ëng
cña kÝch th−íc h×nh häc thµnh kªnh. Khu vùc
s¸t thµnh øng suÊt tiÕp trung b×nh do nhít
®éng lùc ph©n tö quyÕt ®Þnh, cã cÊu tróc xo¸y
rêi r¹c ba chiÒu, song dao ®éng n¨ng l−îng
thùc tÕ b»ng kh«ng, dßng trung b×nh lµ dßng
tÇng vµ gäi lµ líp máng ch¶y tÇng:
y
u
dy
du
0y
0μ=μ=τ≈τ
=
(11)
§èi víi dßng ch¶y æn ®Þnh qua thµnh
ph¼ng tr¬n hay dßng hai chiÒu trong kªnh
réng th× cã thÓ chia quy luËt ph©n phèi tèc ®é
u däc theo y thµnh hai quy luËt th«ng dông
(Rouse n¨m 1959, Hinze n¨m 1975,
Schlichting n¨m 1968) lµ quy luËt gÇn thµnh
vµ quy luËt xa thµnh, hai quy luËt kh«ng ®éc
lËp mµ cã khu vùc chång lªn nhau, tøc lµ quy
luËt s¸t thµnh më réng ra ngoµi vµ khu vùc
ngoµi më réng vµo khu vùc s¸t thµnh.
Quy luËt s¸t thµnh:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
δν
=
t
s
*
*
k
;
yu
f
u
u (12)
Quy luËt xa thµnh:
⎟
⎠
⎞
⎜
⎝
⎛
δ
=
−
s
*
max H,
y
f
u
uu (13)
trong ®ã ρ
τ
=0
*
u lµ tèc ®é ®éng lùc cã
®¬n vÞ lµ m/s; ν = ρ
μ lµ hÖ sè nhít ®éng;
ρ
lµ
mËt ®é chÊt láng; tèc ®é dßng ngoµi líp
biªn; lµ chiÒu dµy líp biªn; H
max
u
δs lµ yÕu tè h×nh
d¹ng kh«ng ®¬n vÞ g¾n liÒn víi sù thay ®æi ¸p
suÊt vµ sè Rex vµ th−êng lµ tû sè cña *
δ
& θ.
Khu vùc cã quy luËt logarit trong ph¹m vi
τ
500
yu
50 *≤
ν
≤ giíi h¹n trªn phô thuéc vµo
ν
δ
max
u. Thùc tÕ kh«ng cã ph−¬ng tr×nh nμo
m« t¶ thay ®æi tèc ®é trong ph¹m vi
50
yu
5*≤
ν
≤. §©y lµ khu vùc ph©n phèi tèc ®é
thay ®æi tõ tõ, tõ quy luËt tuyÕn tÝnh ®Õn quy
luËt logarit. Trong khu vùc hai quy luËt chËp
nhau, Rouse(n¨m 1959) ®Ò nghÞ quy luËt
logarit ph©n phèi tèc ®é:
2
*
1
*
C
yu
lgC
u
u+
ν
= (14)
Chen C. L (1991) ®Ò ngÞ quy luËt sè mò:
m
*
3
*
yu
C
u
u⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ν
= (15)
C1, C2, C3 lµ h»ng sè ®èi víi kªnh cô thÓ,
m thay ®æi tõ 1/4 ®Õn 1/12 ®èi víi thµnh kh¸c
nhau Prabhta K. Swamee(1993) ®Ò nghÞ biÓu
thøc:
⎪
⎩
⎪
⎨
⎧
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ν
=
−3
10
*
*
yu
u
u
3,0
3
10
s*
*
1
ku3.0
yu9
1lg3.2*K
−
−
−
⎪
⎭
⎪
⎬
⎫
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+ν
++
(16)
tho¶ m·n sè liÖu Nikurades ®èi víi nh¸m
t−¬ng ®èi trong èng ks/d = 0,001 -> 0,033 vµ
sè liÖu thÝ nghiÖm cña Lindgren (White 1974).
Khu vùc chËp nhau thay ®æi tõ 30
yu*=
ν
(Rouse n¨m 1959, Hinze n¨m 1975) ®Õn = 70
(Schlichting), tøc lµ 70
yu
30 *≤
ν
≤. KÕt hîp
(11) vµ (12) rót ra quan hÖ khi 4
yu
0*≤
ν
≤ lµ:
dν
=yu
u
u*
*
(17)
Do viÖc trùc tiÕp ®o
τ
gÆp rÊt nhiÒu khã
kh¨n nªn ng−êi ta th−êng ®o tèc ®é rèi sö
dông c«ng thøc (14) – (15) ®Ó tÝnh . YÕu tè
τ
h×nh d¹ng Hs ë (13) chØ ra h»ng sè C1, C2 vµ
phô thuéc vµo kÝch th−íc h×nh häc cña
kªnh. §èi víi dßng ch¶y æn ®Þnh ®Òu trong
èng vµ dßng ch¶y hai chiÒu trong kªnh, (12)
vµ (13) khi ®èi chiÕu víi (1) thÓ hiÖn lùc kh¸ng
chØ lµ hµm cña Re vµ k
0
τ
s/R khi bá qua ¶nh
h−ëng cña Fr.
f, ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=R
k
Re,f
g
c
,
R
ns
6
1 (18)
ThÝ dô quan hÖ (18) ®−îc thÓ hiÖn b»ng
c«ng thøc Blasius(1913) cho èng tr¬n khi
:
5
10Re4000 ≤≤ 25.0
Re
3164.0
f= (19)
C«ng thøc Filonenko vµ Altshul ®èi víi
nh¸m tù nhiªn:
()
2
tr 64.1Relg14.4f −
−= (20)
C«ng thøc Conacop(1947) cho thµnh tr¬n
khi Re :
5
10≥
(
2
tr 5.1Relg8.1f −
−=
)
(21)
C«ng thøc Nikurade (1933):
(
)
8.0fRelg2f tr
1
tr −=
− (22)
Khi 5x103 < Re < 4x107. Khi Re > 25000
c«ng thøc Colebrook - White cã d¹ng:
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+−=
−
fRe4
K
RK
k
lgKf 3
2
s
1
1 (23)
ThÝ dô K1 = 2,0; K2 = 12,0; K3 = 2,5 cho
kªnh réng (Henderson, 1966) hay K1 = 2,0;
K
2 = 12,9; K3 = 2,77 còng cho kªnh réng
(Graf, 1971). §Ó tr¸nh ph¶i thö dÇn theo (23)
ng−êi ta th−êng sö dông trong thùc hµnh c«ng
thøc cho dßng ch¶y ®Çy èng cña (Barr, 1972.
Churchill 1973, Barr 1977) (Barr sö dông sè
mò 0,89 thay cho 0,9 vµ h»ng sè 5,2 cho
5,76).
()
2
9.0
s
Re4
76.5
R8.14
k
lg
4
1
f
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡+
⎟
⎠
⎞
⎜
⎝
⎛
−= (24)
hay c«ng thøc Barr:
()()
()
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+−= 7.0
s
52.0
s
k/d29Re1Re
7Re/lg518.4Relg02.5
d7.3
k
lg2
f
1
(25)
Yªn (1991) ®Ò nghÞ c«ng thøc kªnh réng
khi Re > 30000 vµ ks/R < 0,05:
2
9.0
s
Re
95.1
R12
k
lg
4
1
f
−
⎥
⎦
⎤
⎢
⎣
⎡⎟
⎠
⎞
⎜
⎝
⎛+−= (26)
Quan hÖ (18) còng lµ c¬ së cho to¸n ®å
cña Moody (1944); cña to¸n ®å ®Ó thiÕt kÕ
kªnh vµ ®−êng èng cña tr¹m nghiªn cøu thuû
lùc (HRS, n¨m 1978).
3. Quan ®iÓm thùc tÕ ®èi víi c¸c hÖ
sè n, C, f
Cho tíi nay ch−a cã mét tiÕn bé nµo vÒ lý
thuyÕt gi¶i quyÕt vÊn ®Ò vÒ hÖ sè lùc c¶n ®Ó
thay thÕ cho n, C vµ f, vÉn sö dông c¸ch tiÕp
cËn theo quan ®iÓm ®éng l−îng hay n¨ng
l−îng mµ biÓu thøc quan hÖ gi−· chóng lµ (6).
VÒ mÆt c¬ häc chÊt láng, f liªn quan trùc tiÕp
®Õn nhËn thøc vÒ ®éng l−îng, song kü s− thuû
lùc hay kü s− cã liªn quan ®Õn thuû lùc l¹i coi
f’ lµ hÖ sè tæn thÊt n¨ng l−îng. VËy cã thÓ coi f
nh− lµ hÖ sè søc c¶n t¹i mét ®iÓm quan hÖ víi
ph©n phèi tèc ®é dï r»ng kü s− thuû lùc më
réng quan niÖm nµy tíi toµn mÆt c¾t hay ®o¹n
dßng ch¶y vµ lµ hÖ sè tæn thÊt n¨ng l−îng. HÖ
sè C lµ d¹ng ®¬n gi¶n nhÊt vµ ®· ®−îc biÕt tõ
l©u, trong ®ã ph¶i kÓ ®Õn ®ãng gãp quan träng
cña N. N. Pavlovski vµ nhiÒu t¸c gi¶ kh¸c,
song l¹i kh«ng cã b¶ng tæng qu¸t hay biÓu ®å
tæng qu¸t nµo cho C bëi tÝnh phøc t¹p cña lùc
c¶n n»m ngay trong b¶n chÊt cña vÊn ®Ò.
C«ng thøc Maning x¸c ®Þnh th«ng qua sè liÖu
hiÖn tr−êng rót ra tõ nhËn thøc vÒ tæn thÊt
n¨ng l−îng hay tæn thÊt cét n−íc ®èi víi mét
®o¹n dßng ch¶y. KÕt qu¶ ®o ®¹c hiÖn tr−êng
vµ kinh nghiÖm thùc tÕ trong nh÷ng n¨m qua
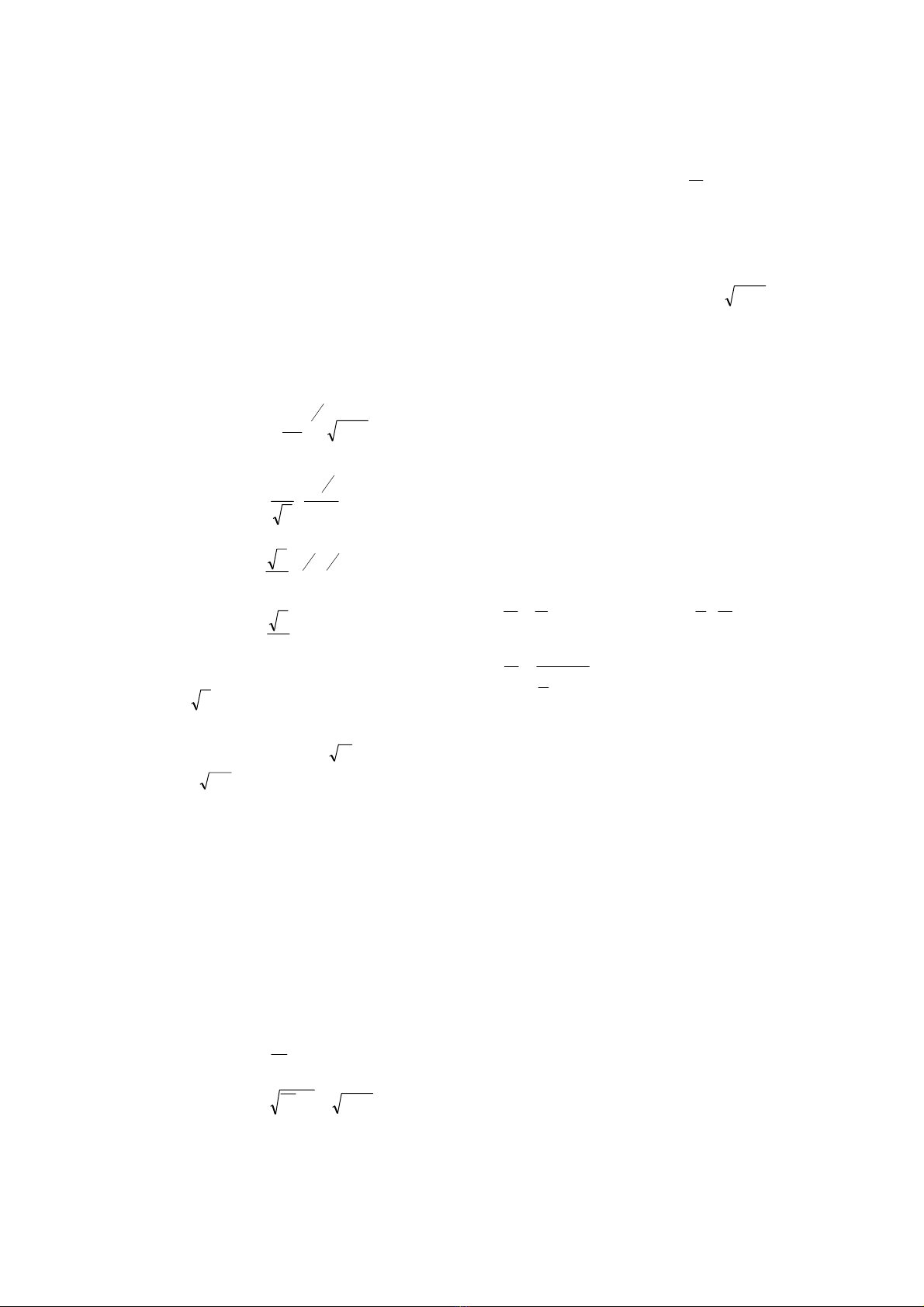
cho thÊy hÖ sè nh¸m n lµ hÖ sè ®¬n gi¶n h¬n
®Ó ®iÒu tiÕt vµ tho¶ m·n c¸c ¶nh h−ëng cña
c¸c th«ng sè kh¸c trong quan hÖ (1) bæ sung
cho sè Reynolds vµ nh¸m t−¬ng ®èi. ChÝnh v×
vËy mµ hiÖn nay cã mét sè b¶ng thÓ hiÖn
quan hÖ gi÷a ks vµ n, ch¼ng h¹n b¶ng quan
hÖ ks ~ n cña Chow (1959). Tõ quan niÖm c¬
häc chÊt láng th× c«ng thøc Maning kh«ng
®ång nhÊt vÒ thø nguyªn, do ®ã Mostafa&
Mcdermid (1971) Dooge (1991), Yen(1991,
1992) ®Ò nghÞ:
gRS
k
R
MV 6
1
s⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
= (27)
trong ®ã: ⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=n
k
g
1
M6
1
s, hay:
2
1
3
2
g
SR
n
g
V= (28)
n
g
ng=
Γ. V. Jelezniakov sö dông hÖ sè C ë
d¹ng C/ g ®Ó gi¶i quyÕt hÖ sè C vµ tÝnh sè
mò y trong c«ng thøc Pavlovski nh−ng cuèi
cïng hÖ sè C vÉn cã ®¬n vÞ S/m ®Ó tÝnh tèc
®é: RSCV =
4. VÊn ®Ò tèc ®é
Thùc tÕ trong tÝnh thuû lùc ta th−êng ph¶i
®o tÝnh tõ mÆt c¾t nµy ®Õn mÆt c¾t kh¸c, tõ
®o¹n kªnh nµy ®Õn ®o¹n kªnh kh¸c däc theo
kªnh ®Ó x¸c ®Þnh c¸c yÕu tè mÆt c¾t, thuû lùc
vµ lùc c¶n do ®ã vai trß cña c¸c yÕu tè
η
vµ N
cña (1) ®−îc thÓ hiÖn. Kh¸i niÖm ®iÓm cña
mÆt thµnh kªnh ph¶i chÞu ¶nh h−ëng cña m«i
tr−êng xung quanh, thÝ dô nh− (14) vµ (15).
Trong dßng ch¶y ®Òu cña kªnh l¨ng trô, øng
suÊt tiÕp trung b×nh RS
0γ=τ do ®ã:
gRS/u 0* =ρτ=
Song trong dßng ch¶y kh«ng ®Òu hay
trong kªnh kh«ng l¨ng trô th× RS
oγ≠τ v× sù
thay ®æi ¸p suÊt vµ vai trß cña thµnh phÇn ¸p
suÊt däc theo dßng ch¶y t¸c dông lªn thµnh
kªnh.
Sè h¹ng cuèi cïng cña (6) lµ V/gRS
th−êng ®−îc viÕt lµ u*/V. u* ®−îc ®inh nghÜa vµ
x¸c ®Þnh theo nhiÒu c¸ch, ch¼ng h¹n nh− rót
ra tõ ®o trùc tiÕp, 0
tÝnh tõ ph©n phèi tèc ®é,
tõ quan hÖ thuû lùc th«ng qua ®é dèc thuû lùc
vµ thÕ n¨ng (®iÓm, mÆt c¾t, dßng ch¶y). Tèc
®é trung b×nh theo chiÒu s©u Vh ph¶i ®−îc rót
ra tõ tæng cña hai tÝch ph©n quy luËt ph©n phèi
tèc ®é gÇn thµnh vµ xa thµnh. Thùc tÕ tèc ®é
lín nhÊt kh«ng ph¶i ë mÆt n−íc, do ®ã chiÒu
s©u h khi lÊy tÝch ph©n còng lµ vÊn ®Ò. Tèc ®é
trung b×nh mÆt c¾t V còng ®−îc ®Þnh nghÜa vµ
x¸c ®Þnh theo nhiÒu c¸ch kh¸c nhau. ThÝ dô:
∫∫
ω
=
ω
=
h
0p
udydp
1Q
V hay ∫ω
=
L
dx
Q
L
1
V hay
∫ω
=
ω
=
L
dx
L
1
QQ
V.
B¸n kÝnh thuû lùc R còng ®−îc tÝnh theo
nhiÒu c¸ch. Nh− vËy cho tíi nay víi quan
niÖm ®éng l−îng tiÕp tuyÕn cã 6 ®Þnh nghÜa
u*, ba ®Þnh nghÜa V vμ m−êi t¸m ®Þnh nghÜa
u*/V, t¹o ra cã m−êi t¸m c¸ch kh¸c nhau
tÝnh gi¸ trÞ trung b×nh cña n hay f ®èi víi
mét ®o¹n kªnh. Cã bèn c¸ch x¸c ®Þnh gi¸
trÞ trung b×nh mÆt c¾t cña n hay f; cã ba
c¸ch x¸c ®Þnh gi¸ trÞ n hay f t¹i mét ®iÓm.
Trong ®ã chØ cã ba tr−êng hîp trïng víi
®Þnh nghÜa cña ph−¬ng tr×nh Maning,
Darcy - Weisbach vμ Chezy thÓ hiÖn ë (6).
Do vËy còng kh«ng ph©n v©n vÒ tÝnh ch−a
thèng nhÊt vμ phøc t¹p, r¾c rèi khi tÝnh hÖ
sè lùc c¶n cña dßng ch¶y. Tuy nhiªn xÐt
theo quan ®iÓm thùc tÕ ta th−êng dïng
ph−¬ng ph¸p n¨ng l−îng ®èi víi mét ®o¹n
dßng ch¶y ®Ó x¸c ®Þnh u*/V nÕu mÆt c¾t ®Çu