Sai sè gãc ®Þnh h−íng vμ chiÒu dμi c¹nh
X¸c ®Þnh trªn thùc ®Þa
TS. trÇn ®¾c sö
Bé m«n Tr¾c ®Þa - §H GTVT
Tãm t¾t: Bμi b¸o giíi thiÖu c«ng thøc tÝnh ¶nh h−ëng sai sè gãc ®Þnh h−íng vμ chiÒu dμi
c¹nh ®−îc x¸c ®Þnh trªn thùc ®Þa khi chuyÓn ®iÓm l−íi khèng chÕ ra khái khu vùc x©y dùng
c«ng tr×nh.
I. §Æt vÊn ®Ò
§Ó x©y dùng c«ng tr×nh ®óng víi ®å ¸n thiÕt kÕ ®ßi hái ph¶i tiÕn hµnh c«ng t¸c tr¾c ®Þa. Mét
trong nh÷ng nhiÖm vô cña c«ng t¸c tr¾c ®Þa nµy lµ thµnh lËp l−íi khèng chÕ tr¾c ®Þa c¬ së,
nh−ng thùc tÕ trong qu¸ tr×nh thi c«ng cã nh÷ng ®iÓm cña l−íi cÇn ph¶i chuyÓn ra khái khu vùc
x©y dùng vµ ph¶i x¸c ®Þnh to¹ ®é cho chóng. §Ó ®¶m b¶o ®é chÝnh x¸c yªu cÇu chóng ta ph¶i
chó ý ®Õn ¶nh h−ëng cña sai sè gãc ®Þnh h−íng vµ chiÒu dµi c¹nh.
II. Néi dung
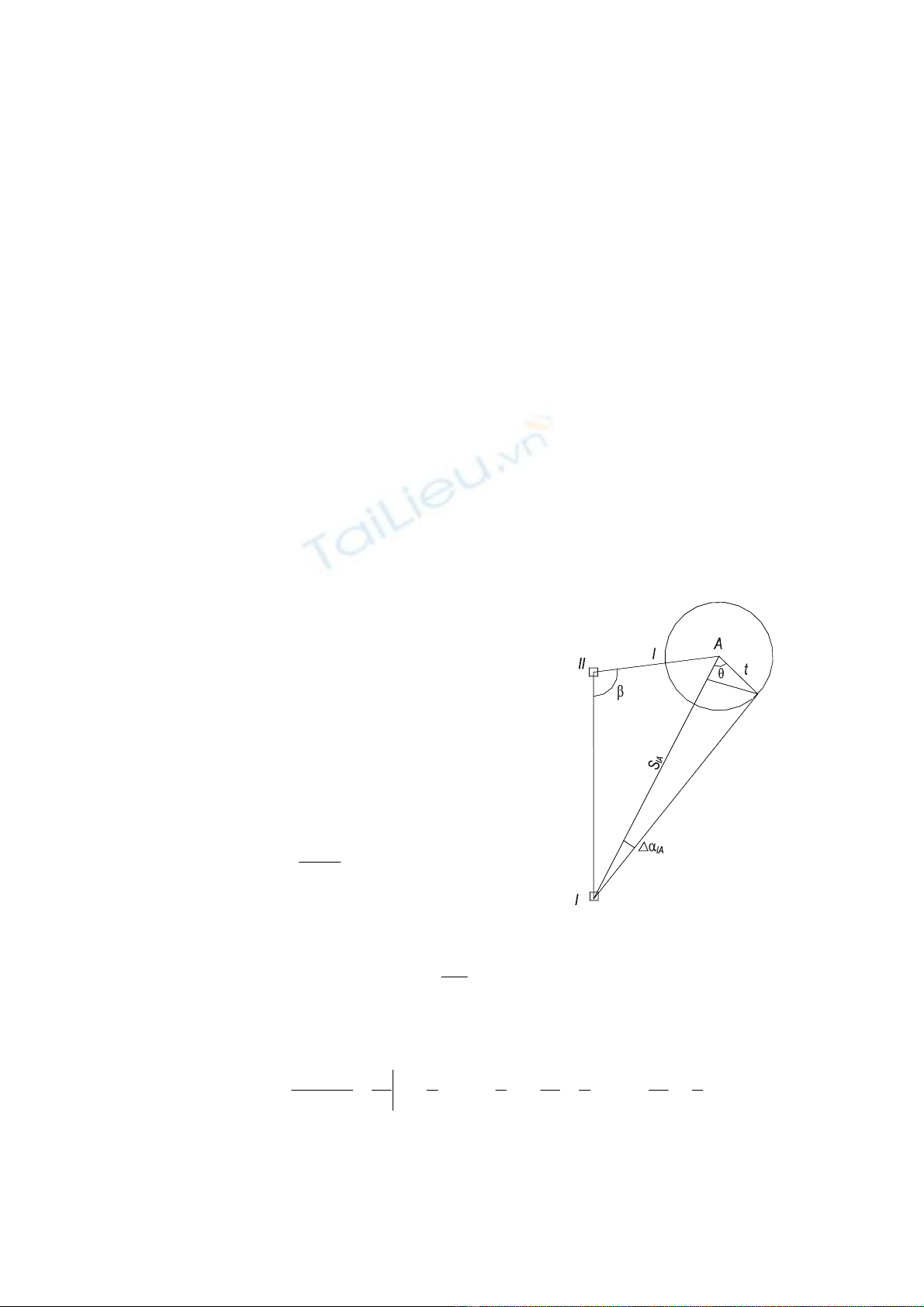
1. Tr−êng hîp x¸c ®Þnh vÞ trÝ ®iÓm A (h×nh 1)
§iÓm A x¸c ®Þnh b»ng ph−¬ng ph¸p to¹ ®é cùc tõ
®iÓm II vµ h−íng II-I (h×nh 1) nh− vËy h−íng IA vµ chiÒu
dµi cña nã sÏ ®−îc x¸c ®Þnh. Do ¶nh h−ëng cña sai sè
®o gãc β vµ chiÒu dµi l ®iÓm A lÖch mét ®o¹n t vµ mét
gãc θ so víi h−íng AI. Gãc θ cã thÓ thay ®æi tõ 00 - 3600.
V× vËy sai sè h−íng IA còng thay ®æi.
Gi¸ trÞ t rÊt nhá v× vËy sai sè ΔαIA gãc ®Þnh h−íng
c¹nh IA cã thÓ biÓu thÞ b»ng c«ng thøc sau:
IA
IA S
sin.t
.θ
ρ=αΔ (1)
Coi , t lµ nh÷ng vi ph©n vµ chuyÓn vÒ sai sè
trung ph−¬ng ta ®−îc:
IA
αΔ
H×nh 1.
θρ=
α
2
2
IA
2
t
22
IA sin.
S
m
.m (2)
Trong ®ã gi¸ trÞ trung b×nh sin2θ ®−îc x¸c ®Þnh:
2
1
)
2
2
4sin
4
1
(
2
1
)
2
1
2Sin
4
1
(
2
1
2
dSin
sin
2
0
2
0
2
2=
π
+π−
π
=θ+θ−
π
=
π
θ
=θ
π
π
∫
(3)
Thay (3) vµo (2) ta cã: 2
IA
2
t
2
2
IA S
m
.
2
mρ
=
α (4)
Sai sè chiÒu dµi c¹nh IA theo h×nh 1 lµ:
θ
=
Δ
cos.t
IA
S (5)
Coi lµ nh÷ng vi ph©n vµ chuyÓn vÒ sai sè trung ph−¬ng ta ®−îc:
t,
IA
S
Δ
θ= 22
t
2
IA
Scos.mm (6)
Trong ®ã gi¸ trÞ trung b×nh Cos2θ ®−îc x¸c ®Þnh:
2
1
)
2
2
4sin
4
1
(
2
1
)
2
1
2sin
4
1
(
2
1
2
dcos
cos
2
0
2
2=
π
+π
π
=θ+θ
π
=
π
θ
=θ
∫
π
(7)
Thay (7) vµo (6): 2
t
2
IA
Sm
2
1
m= (8)
To¹ ®é cña ®iÓm A lµ:
xA = xII + l.cos(αI-II + 1800 - β)
yA = yII + l.sin(αI-I I+ 1800 - β)
trong ®ã: l - kho¶ng c¸ch tõ ®iÓm II ®Õn ®iÓm A; αI-II - gãc ®Þnh h−íng c¹nh I-II; β - gãc cùc.
§iÓm gèc I, II kh«ng cã sai sè vµ αI-II = 00 khi ®ã:
xA = xII - l.cosβ(10)
yA = yII + l.sinβ
LÊy vi ph©n c«ng thøc (10) vµ chuyÓn vÒ sai sè trung ph−¬ng ta ®−îc:
2
2
2222
l
2
A
x
m
.sin.lcos.mm ρ
β+β= β
2
2
2222
l
2
A
y
m
.cos.lsin.mm ρ
β+β= β
(
9
)
(
10
)
(
11
)
A
y
A
xm,m lµ sai sè thµnh phÇn trªn trôc x, trôc y cña ®é lÖch ®iÓm A. V× vËy:
2
A
y
2
A
x
2
tmmm += (12)
Thay (11) vµo (12) ta ®−îc:
2
2
22
l
2
t
m
.lmm ρ
+= β (13)
¸p dông nguyªn t¾c ®ång ¶nh h−ëng ta ®−îc:
lt m.2m =
ρ
=β
m
.l.2mt
Thay (14) vµo (4) ta ®−îc:
IA
l
IA S
m
.m ρ=
α (15)
Thay (14) vµo (8) ta ®−îc: β
ρ
=m.
l
mIA
S (16)
Theo c«ng thøc (12) mt = M - Sai sè trung ph−¬ng vÞ trÝ ®iÓm. Khi ®ã sai sè trung ph−¬ng
h−íng tõ ®iÓm gèc (I) ®Õn ®iÓm x¸c ®Þnh (A) theo c«ng thøc (4) lµ:
IA
IA S
M
.
2
mρ
=
α (17)
Vµ sai sè trung ph−¬ng chiÒu dµi c¹nh IA theo c«ng thøc (8) lµ:
2
M
mIA
S= (18)
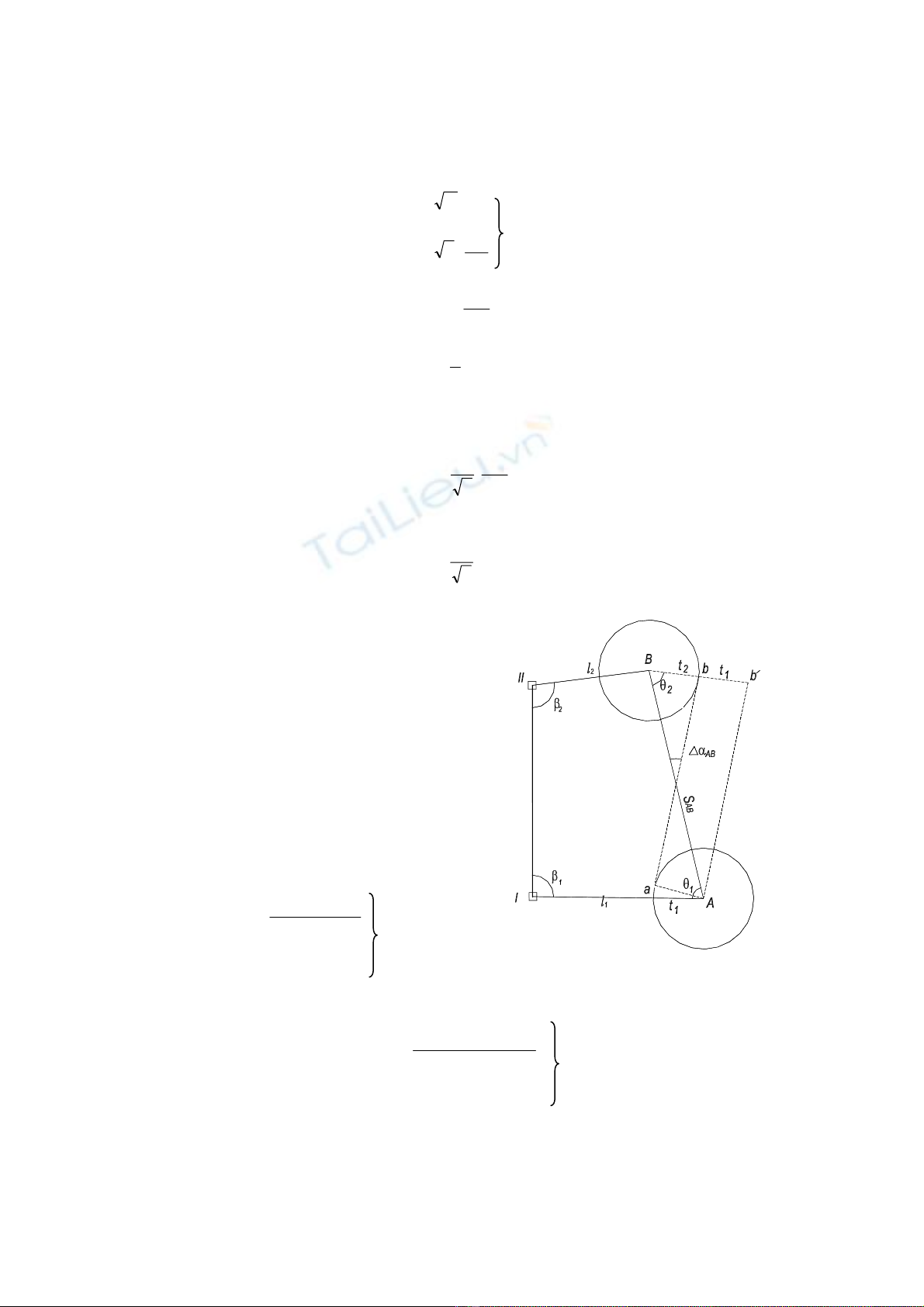
2. Tr−êng hîp x¸c ®Þnh vÞ trÝ ®iÓm A vμ B
(h×nh 2).
Trªn thùc ®Þa tõ hai ®iÓm gèc I vµ II x¸c ®Þnh
®iÓm A vµ B. Sai sè gãc ®Þnh h−íng vµ chiÒu dµi
c¹nh AB cã thÓ thµnh lËp t−¬ng tù nh− trªn.
Gi¶ thiÕt A, B vÞ trÝ ®óng trªn thùc ®Þa vµ t1, t2,
θ1, θ2 - ®é lÖch chiÒu dµi vµ gãc so víi h−íng AB;
- sai sè gãc ®Þnh h−íng míi.
AB
α
Δ
Gi¶ sö θ1 = θ2 = θ vµ tõ A kÎ ®−êng th¼ng
song song víi ab c¾t Bb t¹i b'.
Gi¸ trÞ t1, t2 rÊt nhá so víi SAB v× vËy:
AB
21
AB S
sin).tt(
.θ+
ρ=Δα
θ
+
=Δ cos)tt( 21
AB
S
ChuyÓn (19) vÒ sai sè trung ph−¬ng ta ®−îc:
θ+=
θ+
ρ=
α
22
2t
2
1t
2
AB
S
2
AB
22
2t
2
1t
22
AB
cos).mm(m
S
sin).mm(
.m
(20)
H×nh 2.
(19)
(
14
)
¸p dông c«ng thøc (3), (7)vµ (19) ta ®−îc:
2
mm
m
2
mm
.
S
m
2
2t
2
1t
AB
S
2
2t
2
1t
AB
AB
+
=
+
ρ
=
α
(21)
¸p dông c«ng thøc (14) ta ®−îc:
AB
2
2l
2
1l
AB S
mm.
m+ρ
=
α (22)
NÕu th×:
l
2
l
1
lmmm ==
AB
l
AB S
2m
.m ρ=
α (23)
ρ
+
=ββ 22
2
2
21
2
1
AB
S
mlml
m (24)
NÕu mβ1= mβ2= mβ th×: 2
2
2
1
AB
Sll.
m
m+
ρ
=β (25)
Khi l1 = l2 = l th×: 2.l.
m
mAB
Sρ
=β (26)
Gi¶ thiÕt mt1 = M1, mt2 = M2. Khi ®ã:
2
MM
m
2
MM
.
S
m
2
2
2
1
AB
S
2
2
2
1
AB
AB
+
=
+
ρ
=
α
(27)
Khi M1 = M2 = M th×:
Mm
.
S
M
m
AB
S
AB
AB
=
ρ=
α (28)
III. KÕt luËn
Trªn c¬ së c¸c c«ng thøc ®¸nh gi¸ ®é chÝnh x¸c h−íng vµ chiÒu dµi c¹nh ®−îc x¸c ®Þnh ë
thùc ®Þa khi chuyÓn c¸c ®iÓm l−íi khèng chÕ ra ngoµi khu vùc x©y dùng ®· cho chóng ta kh¶
n¨ng tæ chøc vµ tiÕn hµnh c«ng t¸c tr¾c ®Þa mét c¸ch hîp lý víi ®é chÜnh x¸c yªu cÇu trong mäi
®iÒu kiÖn khã kh¨n cña khu vùc x©y dùng.
Tµi liÖu tham kh¶o
[1] Zacatèp P. X. Tr¾c ®Þa C«ng tr×nh. Matxc¬va, 1976.
[2] Balsacèp V. D; Lepchuc G. P; Novac V. E. TuyÓn tËp Tr¾c ®Þa C«ng tr×nh Matxc¬va 1980¡