Vietnam Journal of Mathematics 33:1 (2005) 97–110
9LHWQDP -RXUQDO
RI
0$7+(0$7,&6
9$67 
N ew C haract erizat ions and G eneralizat ions
of P P R ings
Lix in M ao1,2, N anqing D ing1,andWentingTong
1
1Department of Mathematics, Nanjing University,
Nanjing 210093, P. R. China
2Department of Basi c Courses, Nanji ng I nsti tute of Technology,
Nanjing 210013, P.R. China
Received Febuary 8, 2004
Revised December 28, 2004
A bst ract . T his pap er consist s of t wo part s. In t he first p art , it is proven t h at a ring
Ris right PP if and only if every right R-module has a monic PI -cover, where PI
denot es t he class of all P-inject ive right R-modules. In t he secon d part , for a non -
empt y subset Xof a ring R, we int roduce t he not ion of X-PP rings which unifies PP
rings, PS rings an d nonsin gular rings. Sp ecial at t ent ion is paid t o J-PP rings, where
Jis t he J acob son radical of R. It is shown t hat right J-PP rings lie st rict ly b et ween
right PP rings and right PS rings. Som e new charact erizat ions of (von Neumann)
regular rings and sem isimple Art in ian rings are also given .
1. Int ro d uct ion
AringRis called right PP if every principal right ideal is project ive, or equiva-
lently t he right annihilator of any element of Ris a summand of RR.PP rings
and t heir generalizations have been st udied in many papers such as [4, 9, 10, 12,
13, 21].
In Sec. 2 of this paper, some new charact erizat ions of PP rings are given. We
prove that a ring Ris right PP if and only if every right R-module has a monic
PI -cover if and only if PI is closed under cokernels of monomorphisms and
E(M)/ M is P-inject ive for every cyclically covered right R-module M,where
PI denot es the class of all P-inject ive right R-modules.
In Sec. 3, we first int roduce t he not ion of X-PP rings which unifies PP
98 Lixin Mao, Nanqi ng Ding, and Wenting Tong
rings, PS rings and nonsingular rings, where Xis a non-empty subset of a ring
R. Special at tent ion is paid to t he case X=J, the J acobson radical of R.It
is shown that right J-PP rings lie st rictly between right PP rings and right
PS rings. Some results which are known for PP rings will be proved to hold
for J-PP rings. T hen some new charact erizat ions of (von Neumann) regular
rings and semisimple Artinian rings are also given. For example, it is proven
that Ris regular if and only if Ris right J-PP and right weakly cont inuous if
and only if every right R-module has a PI -envelope wit h the unique mapping
property if and only if PI is closed under cokernels of monomorphisms and every
cyclically covered right R-module is P-injective; Ris semisimple Art inian if and
only if Ris a right J-PP and right (or left) Kasch ring if and only if every right
R-module has an inject ive envelope wit h t he unique mapping property if and
only if every cyclic right R-module is both cyclically covered and P-inject ive.
Finally, we get t hat Ris right PS if and only if every quotient module of any
mininject ive right R-module is mininject ive. Moreover, for an Abelian ring R,it
is obt ained that Ris a right PS ring if and only if every divisible right R-module
is mininject ive, and we conclude this paper by giving an example t o show that
there is a non-Abelian right PS ring in which not every divisible right R-module
is mininject ive.
Throughout , Ris an associat ive ring wit h ident ity and all modules are uni-
tary. We use MRt o indicat e a right R-module. As usual, E(MR) st ands for t he
inject ive envelope of MR,andpd(MR) denot es the project ive dimension of MR.
We wr it e J=J(R), Zr=Z(RR)andSr=Soc(RR) for t he J acobson radical,
the right singular ideal and t he right socle of R, respect ively. For a subset Xof R,
the left (right ) annihilator of Xin Ris denoted by l(X)(r(X)). If X={a},we
usually abbreviat e it t o l(a)(r(a)). We use KeN,K
m ax Nand K
⊕Nto
indicat e that Kis an essent ial submodule, maximal submodule and summand of
N, respect ively. Hom(M , N )(Ext
n(M , N )) means HomR(M , N )(Ext
n
R(M , N ))
for an int eger n≥1. General background mat erial can be found in [1, 6, 18, 20].
2. N ew Characterizat ions of P P R ings
We start with some definitions.
Apair(F,C)ofclassesofright R-modules is called a cotorsion theory [6]
if F⊥=Cand ⊥C=F,whereF⊥={C:Ext
1(F, C) = 0 for all F∈F},and
⊥C={F:Ext
1(F, C) = 0 for all C∈C}.
Let Cbe a class of right R-modules and Maright R-module. A homomor-
phism φ:M→Fwit h F∈Cis called a C-preenvelope of M[6] if for any
homomorphism f:M→F′with F′∈C, there is a homomorphism g:F→F′
such that gφ =f. Moreover, if t he only such gare aut omorphisms of Fwhen
F′=Fand f=φ,theC-preenvelope φis called a C-envelope of M. Following
[6, Definition 7.1.6], a monomorphism α:M→Cwit h C∈Cis said t o be
aspecial C-preenvelope of Mif coker(α)∈⊥C. Dually we have t he definit ions
of a (special) C-precover and a C-cover. Special C-preenvelopes (resp., special
C-precovers) are obviously C-preenvelopes (resp., C-precovers).
Let Mbe a right R-module. Mis called cyclically presented [20, p.342] if it
New Character i zati ons and Generali zati ons of PP Ri ngs 99
is isomorphic t o a fact or module of Rby a cyclic right ideal. Mis P-injective
[14] if Ext1(N , M ) = 0 for any cyclically present ed right R-module N.Mis
called cyclically covered if Mis a summand in a right R-module Nsuch that
Nis a union of a continuous chain, (Nα:α < λ), for a cardinal λ,N0= 0,
and Nα+ 1 / N αis a cyclically present ed right R-module for all α < λ (see [19,
Definition 3.3]).
Denote by CC (PI ) the class of all cyclically covered (P-inject ive) right
R-modules. Then (CC,PI ) is a complet e cotorsion t heory by [19, Theorem
3.4] (note that P-inject ive modules are exact ly divisible modules in [19]). In
part icular, every right R-module has a special PI -preenvelope and a special
CC-precover.
To prove the main theorem, we need t he following lemma.
Lem m a 2.1. Let PI be closed under cokernels of m onomorphisms. If M∈CC,
then Extn(M , N )= 0for any N∈PI and any integer n≥1.
Proof. F or a n y P-inject ive right R-module N, there is an exact sequence 0 →
N→E→L→0, where Eis inject ive. T hen Ext 1(M , L)→Ext 2(M , N )→0
is exact . Not e t hat Lis P-inject ive by hypothesis, so Ext1(M , L)= 0. Thus
Ext 2(M , N )= 0,and hence the result holds by induct ion.
We are now in a position t o prove
T heorem 2.2. T he following are equivalent for a ring R:
(1) Ris a right PP ring;
(2) Every quotient module of any (P-)injective right R-module is P-injective;
(3) Every (quotient module of any injective) right R-m odule Mhas a m onic
PI -cover φ:F→M;
(4) PI is closed under cokernels of monom orphisms, and every cyclically cov-
ered right R-m odule Mhas a m onic PI -cover φ:F→M;
(5) PI is closed under cokernels of monom orphisms, and pd(M)1for every
cy clically covered ( cy clically presen t ed) right R-module M;
(6) PI is closed under cokernels of monomorphisms, and E(M)/ M is P-injective
for every cyclically covered right R-module M.
Proof.
(1) ⇔(2) holds by [21, T heorem 2].
(2) ⇒(3). Let Mbe any right R-module. Writ e F=
{NM:N∈PI}
and G=⊕ { NM:N∈PI}. Then t here exist s an exact sequence 0 →
K→G→F→0. Not e t hat G∈PI,soF∈PI by (2). Next we prove that
the inclusion i:F→Mis a PI -cover of M.Letψ:F′→Mwit h F′∈PI
be an arbitrary right R-homomorphism. Note t hat ψ(F′)Fby (2). Define
ζ:F′→Fvia ζ(x)= ψ(x)forx∈F′.Theni ζ =ψ,andsoi:F→Mis a
PI -precover of M. In addit ion, it is clear that the ident ity map IFof Fis the
only homomorphism g:F→Fsuch that i g =i, and hence (3) follows.
(3) ⇒(2). Let Mbe any P-inject ive right R-module and Nany submodule
of M.WeshallshowthatM / N is P-inject ive. Indeed, t here exist s an exact
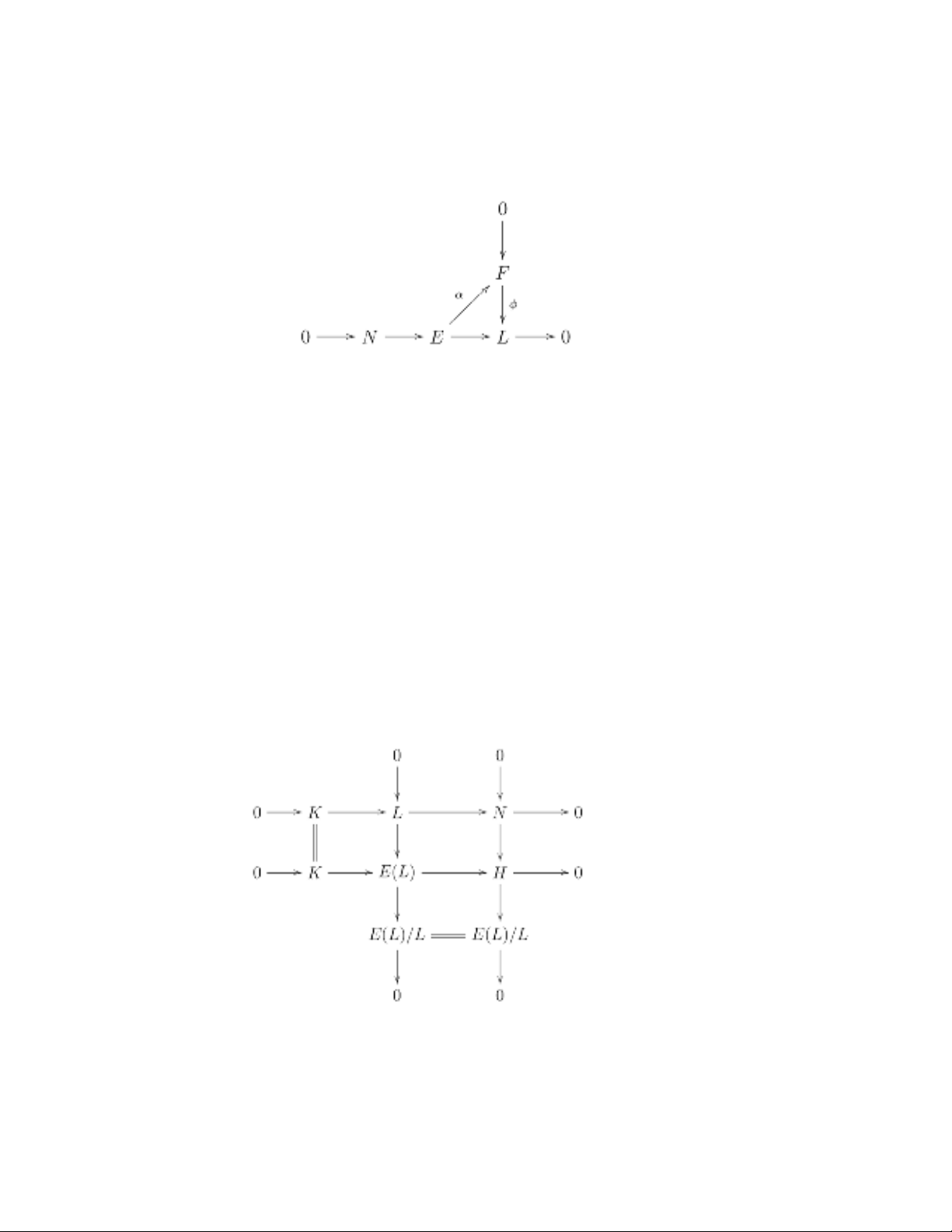
100 Li xin Mao, Nanqing Ding, and Wenting Tong
sequence 0 →N→E→L→0withEinject ive. Since Lhas a monic PI -cover
φ:F→Lby (3), there is α:E→Fsuch t hat t he following exact diagram is
commutat ive:
Thus φis epic, and hence it is an isomorphism. T herefore Lis P-inject ive. For
any cyclically present ed right R-module K,wehave
0= Ext
1(K , L )→Ext2(K , N )→Ext 2(K , E )= 0.
Therefore Ext 2(K , N ) = 0. On the ot her hand, the short exact sequence 0 →
N→M→M / N →0 induces t he exact ness of t he sequence
0= Ext
1(K , M )→Ext1(K , M / N )→Ext2(K , N )= 0.
Therefore Ext1(K , M / N ) = 0, as desired.
(3) ⇒(4) and (2) ⇒(6) are clear.
(4) ⇒(2). Let Mbe any P-inject ive right R-module and Nany submodule
of M.WehavetoprovethatM / N is P-inject ive. Not e t hat Nhas a special
PI -preenvelope, i.e., t here exist s an exact sequence 0 →N→E→L→0with
E∈PI and L∈CC. T he rest of the proof is similar to that of (3) ⇒(2) by
not ing that Ext2(K , E ) = 0 for any cyclically present ed right R-module Kby
Lemma 2.1.
(6) ⇒(2). Let Mbe any P-inject ive right R-module and Nany submodule of
M.NotethatNhas a special CC-precover, i.e., there exist s an exact sequence
0→K→L→N→0withK∈PI and L∈CC. We have the following
pushout diagram
New Character i zati ons and Generali zati ons of PP Ri ngs 101
Since Kand E(L)areP-inject ive, so is Hby (6). Not e that E(L)/ L is P-
injective by (6). T hus (6) ⇒(2) follows from t he proof of (3) ⇒(2) and Lemma
2.1.
(2) ⇒(5). Let Mbe a cyclically covered right R-module. T hen Madmit s a
project ive resolut ion
···→ Pn→Pn−1→ ···P1→P0→M→0.
Let Nbe any right R-module. There is an exact sequence
0→N→E→L→0,
where Eand Lare P-inject ive. T herefore we form the following double complex
00 0
↑↑ ↑
0→Hom(M , L)→Hom(P0,L)→ ··· →Hom(Pn,L)→ ···
↑↑ ↑
0→Hom(M , E )→Hom(P0,E)→ ··· →Hom(Pn,E)→ ···
↑↑ ↑
0→Hom(P0,N)→ ··· →Hom(Pn,N)→ ···
↑↑
00
Not e that , by Lemma 2.1, all rows are exact except for the bot tom row since
Mis cyclically covered, Eand Lare P-injective, also not e t hat all columns are
exact except for t he left column since all Piare project ive.
Using a spectral sequence argument , we know that the following two com-
plexes
0→Hom(P0,N)→Hom(P1,N)→ ···→ Hom(Pn,N)→ ···
and
0→Hom(M , E )→Hom(M , L)→0
have isomorphic homology groups. Thus Extj(M , N ) = 0 for all j≥2, and
hence pd(M)1.
(5) ⇒(1). For any principal right ideal Iof R, consider the exact sequence
0→I→R→R/ I →0. Since pd(R/ I )1by(5),Iis project ive. So Ris a
right PP ring. T his complet es t he proof.
If Ris an integral domain, then Ris a Dedekind ring if and only if every
cyclic R-module is a summand of a direct sum of cyclically present ed modules
[20, 40.5]. Here we generalize the result to t he following
P ro p osit io n 2.3. Let Rbe a ring such that every cyclic right R-m odule is
cyclically covered. T hen the following are equivalent:
(1) Ris a right PP ring;
(2) Ris a right hereditary ring.