T
ẠP CHÍ KHOA HỌC
TRƯ
ỜNG ĐẠI HỌC SƯ PHẠM TP HỒ CHÍ MINH
Tập 21, Số 2 (2024): 256-263
HO CHI MINH CITY UNIVERSITY OF EDUCATION
JOURNAL OF SCIENCE
Vol. 21, No. 2 (2024): 256-263
ISSN:
2734-9918
Websit
e: https://journal.hcmue.edu.vn https://doi.org/10.54607/hcmue.js.21.2.4072(2024)
256
Bài báo nghiên cứu1
BẤT ĐẲNG THỨC HARNACK YẾU CHO TOÁN TỬ LOẠI SCHRODINGER
Nguyễn Đức Trung*, Nguyễn Trọng Nhân,
Trương Lê Gia Khánh, Nguyễn Ngọc Hữu Ân, Nguyễn Thủy Tiên
Trường Đại học Sư phạm Thành phố Hồ Chí Minh, Việt Nam
*Tác giả liên hệ: Nguyễn Đức Trung – Email: nguyenductrung2282002@gmail.com
Ngày nhận bài: 22-12-2023; ngày nhận bài sửa: 01-02-2024; ngày duyệt đăng: 20-02-2024
TÓM TẮT
Trong lí thuyết chính quy, bất đẳng thức Harnack yếu đóng vai trò quan trọng. Bất đẳng thức
Harnack yếu là cần thiết để chứng minh tính liên tục Holder của nghiệm yếu. Trong bài báo này,
chúng tôi chứng minh bất đẳng thức Harnack yếu cho toán tử loại Schrodinger
()div A u Vu− ∇+
,
là một trong những phương trình có nhiều ứng dụng quan trọng trong vật lí cơ học lượng tử, với A
là ma trận hằng và thế năng V thuộc lớp Holder ngược. Để thu được điều đó, chúng tôi cần đến các
đánh giá cho hàm phụ trợ, bất đẳng thức Fefferman-Phong, bất đẳng thức Caccioppoli và bắt đẳng
thức Friedrichs. Trong Shen (1995), ông đã thiết lập bất đẳng thức Hanack yếu cho nghiệm của
phương trình
0u Vu−∆ + =
. Kết quả của chúng tôi là sự tổng quát kết quả đã có của Shen (1995).
Từ khóa: biên Neumann; toán tử loại Schrodinger; Bất đẳng thức Harnack yếu
1. Giới thiệu
Khi xét toán tử Schrodinger, trong bài báo quan trọng và khởi đầu của Shen (1995),
tác giả đã chứng minh bất đẳng thức Harnack yếu cho toán tử loại Schrodinger
V−∆ +
với
thế năng
V
thuộc lớp Holder ngược. Trong bài báo này chúng tôi mở rộng kết quả trên cho
toán tử
()div A u Vu− ∇+
với A là ma trận hằng với điều kiện biên Neumann.
Thế năng V thuộc lớp Holder ngược, được định nghĩa như sau:
Định nghĩa 1.1. Ta nói
V RH∞
∈
khi đó
. Hơn nữa,
()
()
||
LB B
C
V V X dX
B
∞
≤
∫
với mọi quả cầu mở
B
trong
n
.
Với
Q∈∂Ω
tùy ý và
()r diam< ∂Ω
, ta gọi:
{ }
' ''
( , ) ( , ) : , (1 2 )
n nn
ZQr X X X Q r X Q mr= − < − <+
là tọa độ trụ và m là hệ số Lipschitz của biên.
Cite this article as: Nguyen Duc Trung, Nguyen Trong Nhan, Truong Le Gia Khanh, Nguyen Ngoc Huu An, &
Nguyen Thuy Tien (2024). Weak Harnack inequality for Schrodinger operator. Ho Chi Minh City University of
Education Journal of Science, 21(2), 256-263.
Tạp chí Khoa học Trường ĐHSP TPHCM
Tập 21, Số 2 (2024): 256-263
257
Ta sẽ chứng minh bất đẳng thức Harnack yếu cho nghiệm của phương trình
() 0div A u Vu− ∇+ =
trong bài toán sau:
Bài toán: Cho
12p<≤
và
V RH∞
∈
,
Ω
là miền Lipschitz bị chặn và cho
()
p
gL∈ ∂Ω
:
*
()
div( ) 0, trong
. , trên
()
∂Ω
− ∇+ = Ω
∇ = ∂Ω
∇ <∞
p
L
A u Vu
Au g
u
ν
trong đó:
•
.Au g
ν
∇=
trên
∂Ω
theo nghĩa
, ()
lim ( ) () ()
X QX Q
uX Q gQ
ν
→ ∈Γ
∇⋅=
hầu khắp nơi cho
Q∈∂Ω
.
•
()Q
ν
là vectơ pháp tuyến đơn vị hướng ra ngoài biên
∂Ω
.
•
A
là ma trận hằng số cấp
nn×
, đối xứng và eliptic đều. Nghĩa là:
22
1
,0
; (0,1] sao cho
n
ij ji ij i j
ij
aa a
λ λξ ξξ λ ξ
−
=
= ∃∈ ≤ ≤
∑
với mỗi
n
ξ
∈
.
2. Một số kết quả cần thiết
Trong phần này, ta đề cập một số kết quả về các đánh giá liên quan đến thế năng
V
và
hàm
.m
Định lí 2.1. (Shen, 1995, Bổ đề 1.4): Tồn tại
0, 0Cc>>
và
00k>
chỉ phụ thuộc vào
n
và
hằng số
RH
∞
sao cho với mọi
,, n
XY∈
ta có:
a)
(, )~ (,)mV X mV Y
nếu
1
(, )
XY mV X
−≤
.
b)
( )
0
(,) 1 (, ) (, )
k
mV Y C X YmV X mV X≤ +−
.
c)
{ }
( )
00
/1
(, )
(,) .
1 (, ) +
≥+− kk
Cm V X
mV Y
X Y mV X
trong đó
2( ,)
11
( , ) inf 0 : ( ) 1 .
nBXr
m V X V Y dY
rr
−

=>≤


∫
Hệ quả 2.2. (Shen, 1995, Hệ quả 1.5): Với mọi
,n
XY∈
, ta có:
{ }
( )
( )
{ }
0
0
1
1
1
1 (,) 1 ,
1,
k
k
C X YmVY X YmV X
C X YmVY
+
+
+− ≤+−
≤ +−
Tạp chí Khoa học Trường ĐHSP TPHCM
Nguyễn Đức Trung và tgk
258
Định lí 2.3. (Bất đẳng thức Fefferman-Phong) (Shen, 1994, Bổ đề 1.11):
Cho
( )
1
0
n
uC∈
. Khi đó:
( )
2
22
2
() (,) () .
Ω ΩΩ
≤∇ +
∫ ∫∫
u X m V X dX C u dX C u X V X dX
Định lí 2.4. (Bất đẳng thức Caccioppoli) (Kurata & Sugano, 2000, Bổ đề 2.3): Cho
( )
( )
( )
( )
( )
1 1,2 1
00
,2 : ,2
loc loc loc
u H BX R W H BX R∈=
là nghiệm của
div( )Au− ∇+
0Vu =
trên
( )
0,2 .BX R
Với mọi
(0,1),
τ
∈
tồn tại hằng số
0C>
chỉ phụ thuộc vào
n
và
λ
sao cho:
( )
( ) ( )
00
22 2
22
,,
.
(1 )
BX R BX R
C
u V u dX u dX
R
τ
τ
∇+ ≤−
∫∫
Định lí 2.5. (Bất đẳng thức Friedrichs) (Kurata, & Sugano, 2000, Định lí 6.1): Cho
Ω
là
miền Lipschitz bị chặn trong
n
với
2n≤
. Cho
E⊂ ∂Ω
thỏa
() 0E
σ
>
. Khi đó, tồn tai
hằng số
(, , ) 0C Cn E= Ω>
sao cho:
( )
2 22
E
udX C udX ud
σ
ΩΩ
≤∇ +
∫ ∫∫
với mọi
1,2
( ).uW∈Ω
Định lí 2.6. Cho
u
là nghiệm của
div( ) 0A u Vu− ∇+ =
trong
( )
0,2ZX R∩Ω
với mọi
0
X∈Ω
và
0.R>
Giả sử
*2
()uL∇∈
và
0Au
ν
∇⋅ =
trên
( )
0,2ZX R∩Ω
. Khi đó, ta có
đánh giá sau:
( )
0
0
1
2
2
3
,
,2
.
1
sup


∈

≤


∫R
nDX
X DX R
C u dXu R
Chứng minh. Cố định
0R>
. Không mất tính tổng quát, ta giả sử
X∈∂Ω
. Với mỗi
0M>
và
( ) ( )
00
,2 ,2XDXRBXR∈ = ∩Ω
, ta định nghĩa:
( ), khi ( )
() sign( ), còn lai.
−< <
=
M
uX M uX M
vX Mu
và
( ), khi ( )
() .
0, còn lai.
∇ −< <
∇=
M
uX M uX M
vX
Lấy
0
3
,2
c
R
C BX
ϕ
∞


∈



và
0
3
,2
R
D DX

=

. Theo công thức tích phân từng phần, ta có:
( )
( )
( ) ( )
2 22
2
div
div( ) 0.
,.
M D M DM
D
M
D
AA d v Adu v dX
d
Xuv u
v A uX
ϕ ν ϕσ ϕ
ϕ
∂
∇⋅∇ = ∇⋅ − ∇
=− ⋅∇
≤
∫∫
∫
∫
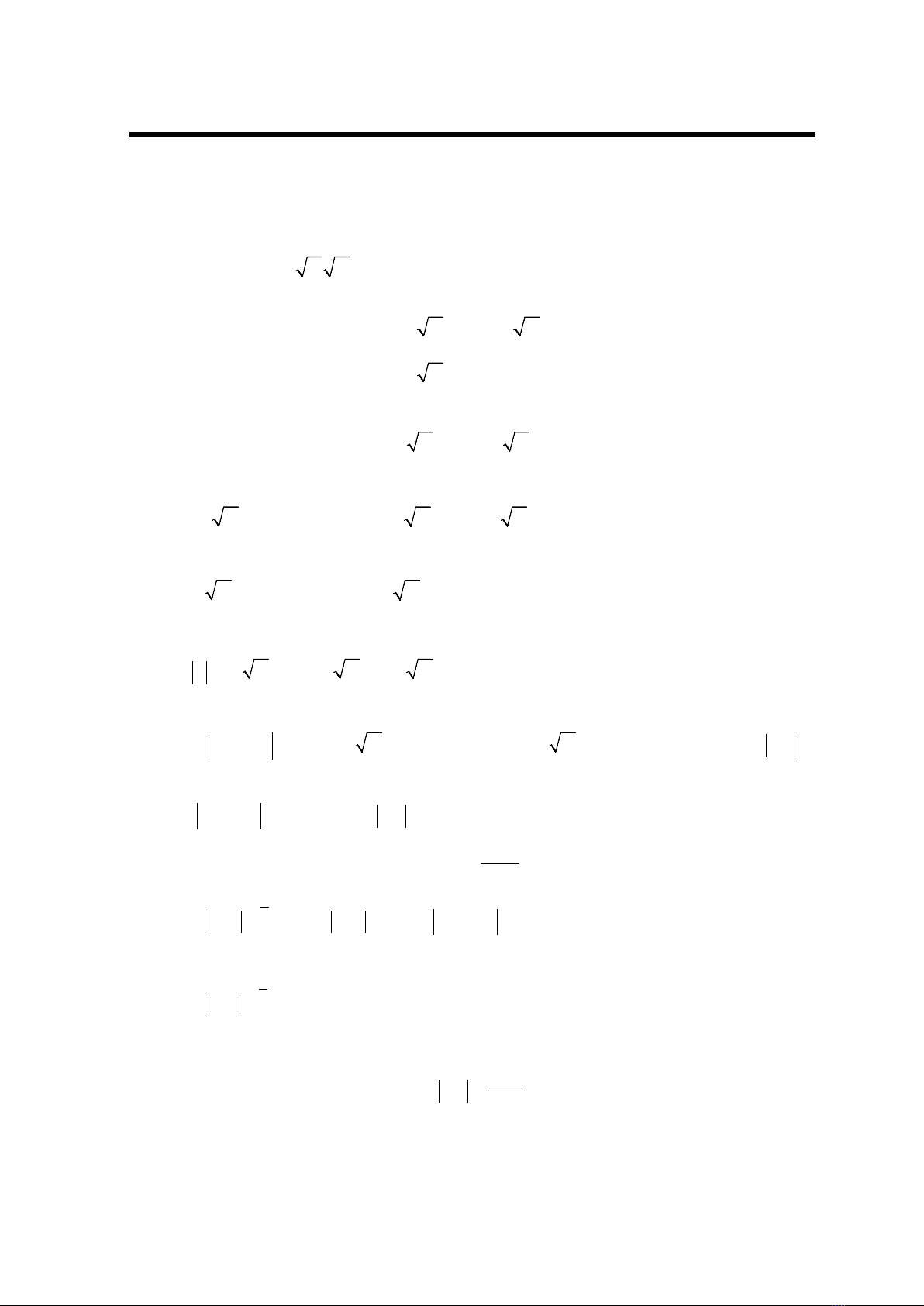
Tạp chí Khoa học Trường ĐHSP TPHCM
Tập 21, Số 2 (2024): 256-263
259
Suy ra,
( ) ( )
2
() 2() 0.
M MM
DD
A u v dX A u v v dX
ϕϕ

∇ ⋅∇ + ∇ ⋅∇ ≤
∫∫
Tiếp theo, ta chéo hóa ma trận
.A
Do
A
đối xứng nên ta có thể viết:
TT
A P EP P E E P= =
trong đó,
E
là ma trận đường chéo và
P
là ma trận trực giao. Ta có:
( ) ( )
( ) ( )
( )
22
2
.
M MM
DD
M
D
A u v dX E P v E P v dX
E P v dX
ϕϕ
ϕ


∇ ⋅∇ = ∇ ⋅ ∇



= ∇

∫∫
∫
Tương tự, ta cũng có:
( )
( ) ( )
.. MMM
DD Au v dX EP v EP dXv
ϕ ϕ ϕϕ
∇ ⋅∇ = ∇
⋅

 
∇
∫∫
Do đó
( ) ( ) ( )
2
2 . 0.
M MM
DD
EP v dX EP v EP v dX
ϕ ϕϕ

∇ + ∇⋅ ∇ ≤

∫∫
Suy ra,
( )
22
() .
MM
DD
E P v dX E P v dX
ϕϕ

∇ ≤ ∇⋅

∫∫
Hơn nữa, theo tính chất eliptic đều, với mọi
,
n
ξ
∈
ta có:
( ) ( )
( )
2
212
| .|EP EP EP A
λξ ξ ξ ξ ξ ξ λ ξ
−

≤ = ⋅ = ⋅≤

Ta suy ra:
( ) ( )
( )
2
2
22
12
..
M M MM
DD D D
v dX E P v dX E P v dX v dX
λϕ ϕ ϕ λ ϕ
−


∇ ≤∇ ≤ ∇ ≤ ∇


∫∫ ∫ ∫
Vậy
( )
22
22 .
MM
DD
v dX v dX
ϕλ ϕ
−
∇ ≤∇
∫∫
Mặt khác, với phép nhúng Sobolev số mũ
2
2
n
pn
=−
, ta có:
( )
( )
()
22
2pp
M MM
D DD
v C v dX v dX
ϕϕϕ
⋅
≤ +∇
∫ ∫∫
Theo Định lí 2.5, ta có:
( )
( )
2
2
||
pp
MM
DD
v C v dX
ϕϕ
≤∇
∫∫
Ta chọn
( )
( )
0
,
c
C BX s
ϕ
∞
∈
sao cho:
0 1, 1
ϕϕ
≤≤ =
trong
( )
0
,BX t
và
.
C
st
ϕ
∇≤−
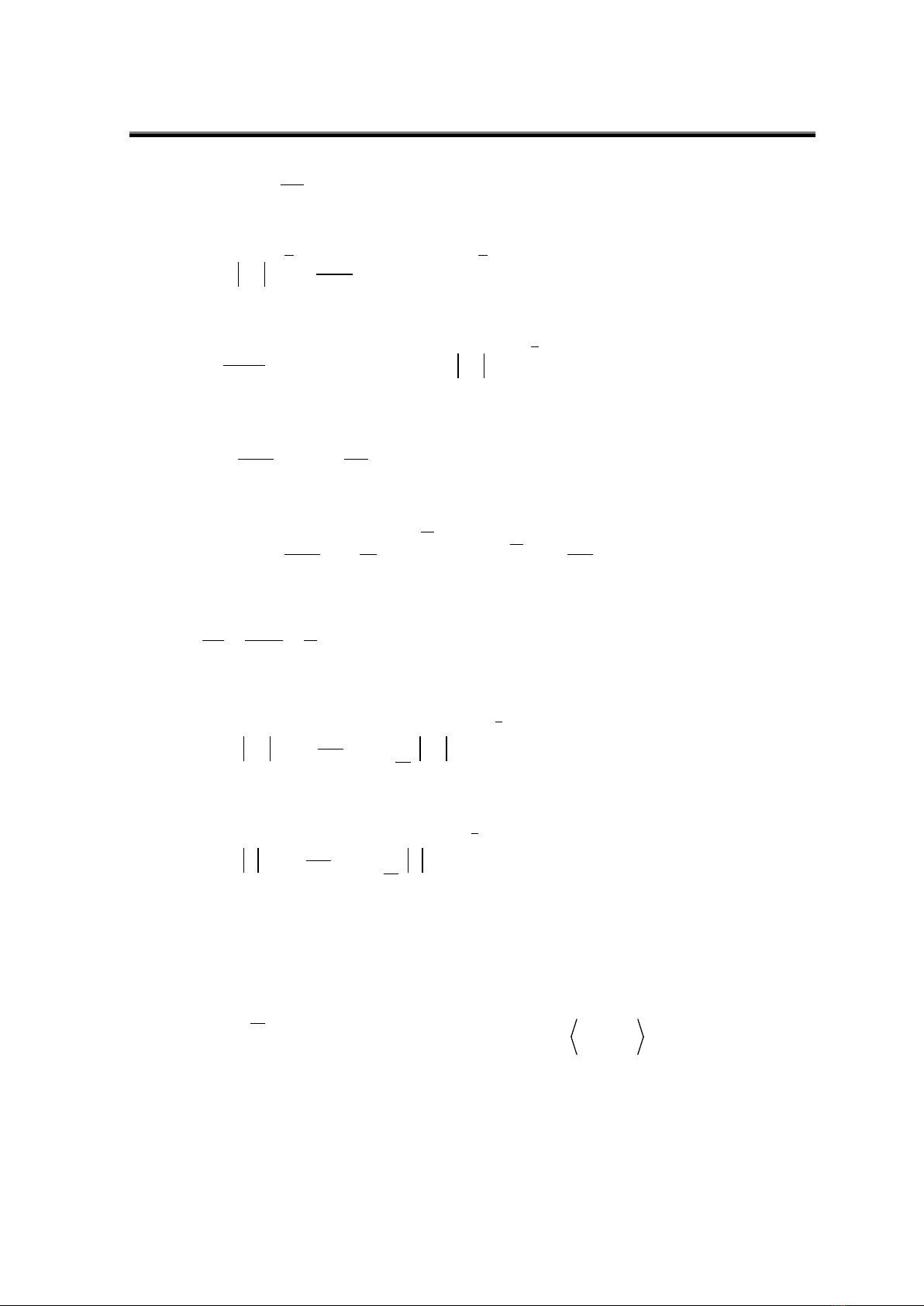
Tạp chí Khoa học Trường ĐHSP TPHCM
Nguyễn Đức Trung và tgk
260
trong đó
3
0.
2
R
ts<<<
Do đó:
( )
( )
( )
( )
00
11
2
,,
pp
p
M M
DX t DX s
C
v v dX
st
≤⋅
−
∫∫
Đặt:
:1
2
n
n
γ
= >
−
và
( )
( )
( )
0
1
,
,: M
q
q
DX t
q t v dX
φ
=∫
( )
1.1
Lặp
( )
1.1
m
lần
( )
m∈
với:
1
;
22
mm
RR
tR sR
+
=+=+
Suy ra,
( )
3
0
0
3
1
1
1
3
2 , 2 2, .
22
m
jm
j
m
m
j
RC R
RR
γγ
φγ γ φ
=
=
+
+
∑

∑
+≤


trong đó,
3
0
1.
12
m
j
n
γ
γγ
=
= =
−
∑
Cho
,m→ +∞
ta được:
( )
0
0
2
1
2
3
,2
,
sp 1
uD
MM
n
XD
R
RX
X
v C v dX
R


∈

≤⋅


∫
Cho
,M→ +∞
ta được:
( )
0
0
2
1
2
3
,2
,
s1
up R
D
n
X DX R X
u C u dX
R


∈

≤⋅


∫
3. Kết luận
Cuối cùng, chúng tôi xây dựng bất đẳng thức Harnack yếu cho toán tử
()div A u Vu− ∇+
thông qua định lí sau đây.
Định lí 3.1. (Harnack yếu): Cho
( )
,0V RH div A u Vu
∞
∈ − ∇+ =
trong
( )
0,2ZX R∩Ω
với mọi
0
X∈Ω
và
0.R>
Giả sử
( )
2
uL
∗
∇∈
và
0A uv∇⋅ =
hay
0u=
trên
( )
0
,2 .ZX R∩ ∂Ω
Thì với mỗi số nguyên dương
k
sẽ tồn tại hằng số
k
C
sao cho: