Bài 3. CÁC BẤT ĐẲNG THỨC LIÊN QUAN TỚI
LŨY THỪA MŨ HỮU TỶ HOẶC MŨ VÔ TỶ
1/Định lý 1.
a-Nếu x -1 và 0 < <1 thì:
(1 + x) ≤ 1 + x (1)
b-Nếu < 0 hoặc > 1 thì:
(1 + x) 1 + x (2)
Dấu bằng ở (1) và (2) xảy ra khi và chỉ khi x = 0.
Chứng minh. a.Trước hết ta giả sử rằng là số hữu tỷ và theo giả thiết 0 < <1. Đặt =
m
n
với m, n là các
số nguyên dương và 1 ≤ m < n. Vì theo giả thiết 1 + x 0 nên
(1 + x) =
1
m
n
x
=
1 .1 1 . 1 ... 1 .1.1...1
mn m
nn
x x x x
m n=m
≤
1 1 ... 1 1 1 ... 1
x x x
n
=
=
1
m x n m
n
=
n mx
n
= 1
m
x
n
= 1 + x
Dấu bằng trong bđt cần chứng minh xảy ra khi và chỉ khi mọi thừa số dưới dấu căn bằng nhau, tức là khi
1+x = 1 x = 0.
Còn nếu x
0 thi
1 1
x x
Như vậy ta đã chứng minh xong (1) với là số hữu tỷ.
Dưới đây ta chứng minh (1) cho trường hợp là số vô tỷ và 0 <<1.
Ta gọi r1, r2, . . ., rn là dãy các số số hữu tỷ mà chúng có giới hạn là . Thêm nữa 0 < rn < 1. Từ bđt
1 1
n
r
n
x r x
, trong đó x -1, n = 1, 2, 3, . .
đã được chứng minh ở trên với trường hợp số mũ hữu tỷ, ta có
1x
lim
1
n
r
x
lim (1+rnx) = 1 + x
rn rn
Bây giờ ta chuyển đến chứng minh bđt (1) với vô tỷ khi x 0 và 0 < < 1
Ta lấy một số hữu tỷ r sao cho < r < 1, khi đó bđt
1
x
có thể viết lại như sau
1
x
=
1
r
r
x
Vì 0 <
r
< 1 nên như ta đã chứng minh ở trên
1 1
r
x x
r
Do đó
1
x
1
r
x
r
Nếu x 0, thì 1
r
x
r
< 1 + r
x
r
= 1 + x tức là
1
x
1 + x phần (a) của định lý 1 đã cm xong!
Ta chuyển đến cm phần b.
b. Nếu 1 + x < 0 thì bđt (2) luôn luôn đúng vì vế trái của nó không âm còn vế phải là một giá trị âm.
Còn nếu 1 + x 0 x -1 thì ta sẽ xét hai trường hợp sau:
b1- Khi > 1 theo phần (a) của định lý đã được cm ở trên, ta có
1
1
x
1
1
x
= 1 + x (3)
Dấu bằng xảy ra khi và chỉ khi x = 0. Nâng cả hai vế của (3) lên lũy thừa , ta được
(1 + x) (1 + x)
b2- Trường hợp thứ hai: Khi < 0.
Nếu 1 + x < 0 thì bđt (2) hiển nhiên đúng.
Còn nếu 1 + x 0 thì ta chọn một số nguyên dương n sao cho
n
< 1.
Do phần (a) của định lý, ta có
1 1
n
x x
n
,
1
1 1
1
n
x x
n
x
n
(4)
(Bất đẳng thức (4) đúng, vì 1 1 -
2
2
2
x
n
), nâng lên lũy thừa n cả hai vế bđt (4) được
1 1 1 1
n
x x n x x
n n
Dấu bằng xảy ra khi và chỉ khi x=0. Trường hợp (b) của định lý đã cm xong.
Và định lý 1 đã được chứng minh xong hoàn toàn!
2/Định lý 2. Nếu a1, a2, . . ., an là các số dương và < thì c c, hơn nữa dấu bằng xảy ra khi và chỉ
khi a1 = a2 = . . . = an.
Với các chỉ só và trái dấu, ta đã chứng minh định lý này ở ví dụ 7 thuộc Bài 2 (“CÁC BẤT ĐẲNG THỨC
KINH ĐIỂN…”). Ở đây, vấn đề còn lại là ta chứng minh định lý với và cùng dấu.
Nhắc lại: c và c là các trung bình lũy thừa mà biểu thức toán học định nghĩa chúng có dạng:
c=
1
1 2 ... n
a a a
n
*Không làm mất tính tổng quát của chứng minh , ta có thể giả sử 0 < < và đặt
k = c =
1
1 2 ... n
a a a
n
Chia c cho k ta có
1
1 2 ... n
a
a a
c c k k k
k c n
(5)
Đến đây, để biểu thức gọn, ta đặt các đại lượng phụ d1 = 1
a
k
, d2 = 2
a
k
, . . ., dn = n
a
k
Khi đó đẳng thức (5) thành
c
k
1
1 2 ... n
d d d
n
(6)
Vì
1
1 2 ... n
d d d
n
=
1
1
1 2
1 2
... ...
1 1
n
n
a
a a
a a a
k k k
c
n k n k
= 1
1
c
c
Nên 1 2 ...
1
n
d d d
n
1 2 ... n
d d d n
(7)
Đặt d1 = 1 + x1, d2 = 1 + x2, . . ., dn = 1 + xn. Từ đẳng thức (7) xuy ra x1 + x2 + . . . +xn = 0.
Dựa trên định lý 1 (nhớ rằng
> 1) ta có:
1 1 1
2 2 2
1 1
1 1
........................................
1 1
n n n
dx x x
d x x
d x x
(8)
Cộng các bđt trên đây vế đối vế ta được:
1 2 1 2
... ...
n n
d d d n x x x
= n (9)
Từ (6) và (9) suy ra:
1
1
cn
c k c
k n
Dấu bằng xảy ra khi và chỉ khi tất cả các bđt trong (8) có dấu bằng, tức là khi x1 = x2 = . . . = xn =0
(theo định lý 1). Trong trường hợp này d1 = d2 = . . . = dn vì vậy a1 = a2 = . . . = an = k.
Còn nếu mọi số a1, a2, . . ., an không bằng nhau thì
c > c
Định lý 2 đã được chứng minh khi 0 <
<
.
* Trường hợp < < 0 thì 0 <
< 1. Đến đây lập luận tương tự như cách chứng minh trên, song lưu ý rằng
trong các bđt (8) và (9) thì dấu bất đẳng thức ngược lại và vì < 0 nên từ bđt
1 2 ...
1
n
d d d
n
suy ra:
1
1
1 2 ...
1
n
cd d d
k n
= 1
Tức là
c
k =
c
định lý 2 đã được chứng minh hoàn toàn!
Đến đây, từ nay trở đi ta có thể gọi trung bình nhân là trung bình lũy thừa cấp 0, nghĩa là g = c0 với > 0.
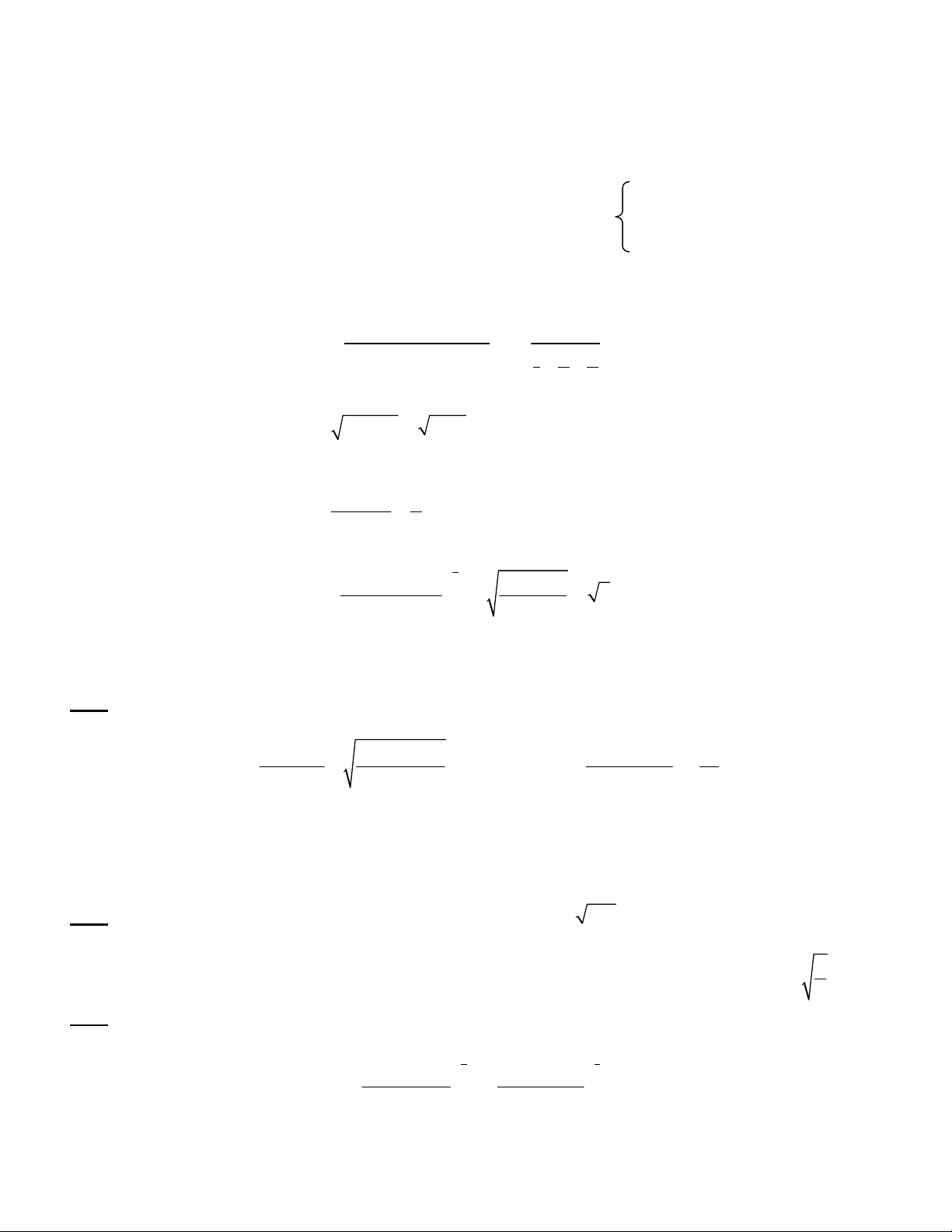
Từ kết quả chứng minh định lý 2, ta suy ra trường hợp đặc biệt sau:
c-1 c0 c1 c2 (10)
Tức là:
Trung bình điều hòa không lớn hơn trung bình nhân,
Trung bình nhân không lớn hơn trung bình cộng, của các số dương.
Trung bình cộng không lớn hơn trung bình bình phương
Ví dụ. a1 = 1, a2 = 2, a3 = 4, ta có:
c-1 =
1
1 1 1
1 2 3
... 3
1 1 1
3
1 2 4
a a a
1,7…
c0 = 3
31 2 3
. . 1.2.4 2
a a a
c1 =
1 2 4 7
3 3
2,3…
c2 =
1
2 2 2 2
1 2 3
3
a a a
1 4 16
7
3
2,6…
Luyện tập 1. Chứng minh rằng x2 + y2 + z2 12 nếu x + y + z = 6
Đáp. Theo kết luận cho bởi bđt (10): Trung bình cộng không lớn hơn trung bình bình phương, ta có
2 2 2
3 3
x y z x y z
2
2 2 2
3
x y z
x y z
=
2
6
3
= 12
Dấu bằng xảy ra khi và chỉ khi x = y = z = 2.
Luyện tập 2. Chứng minh rằng nếu x3 + y3 + z3 = 81 (x > 0, y > 0, z > 0) thì x + y + z 9
Đáp. Vì (x + y + z)3 32(x3 + y3 + z3) = 9.81 = 729 x + y + z 3
729
= 9. Xong!
Luyện tập 3. Chứng minh rằng nếu x, y, z là các số dương và x2 + y2 + z2 = 8 thì x3 + y3 + z3 16
2
3
Đáp. Vì c2 c3, nên
1 1
2 2 2 3 3 3
2 3
3 3
x y z x y z