CHÀO M NG NGÀY NHÀ GIÁO Vi T NAM 20 - 11Ừ Ệ
§ 6. B T PH NG TRÌNH MŨ VÀẤ ƯƠ
B T PH NG TRÌNH LÔGARITẤ ƯƠ
I. B T PH NG TRÌNH MŨẤ ƯƠ
II. B T PH NG TRÌNH LÔGARITẤ ƯƠ
1. B t ph ng trình lôgarit c b nấ ươ ơ ả
Yêu c u:ầ Vi t đ c b ng tóm t t v ế ượ ả ắ ề
t pậ
nghi m c a các bpt lôgarit c b nệ ủ ơ ả
2. B t ph ng trình lôgarit đ n ấ ươ ơ
gi nả
Yêu c u:ầ Gi i và tìm t p nghi m c a ả ậ ệ ủ
các bpt lôgarit đ n gi nơ ả
Th c hi n : ự ệ Nguy n Thanh Lamễ – T Toán Tinổ
Ti t 34ế
TR NG TRUNG H C PH THÔNG THANH BÌNHƯỜ Ọ Ổ
KI M TRA BÀI CŨỂ
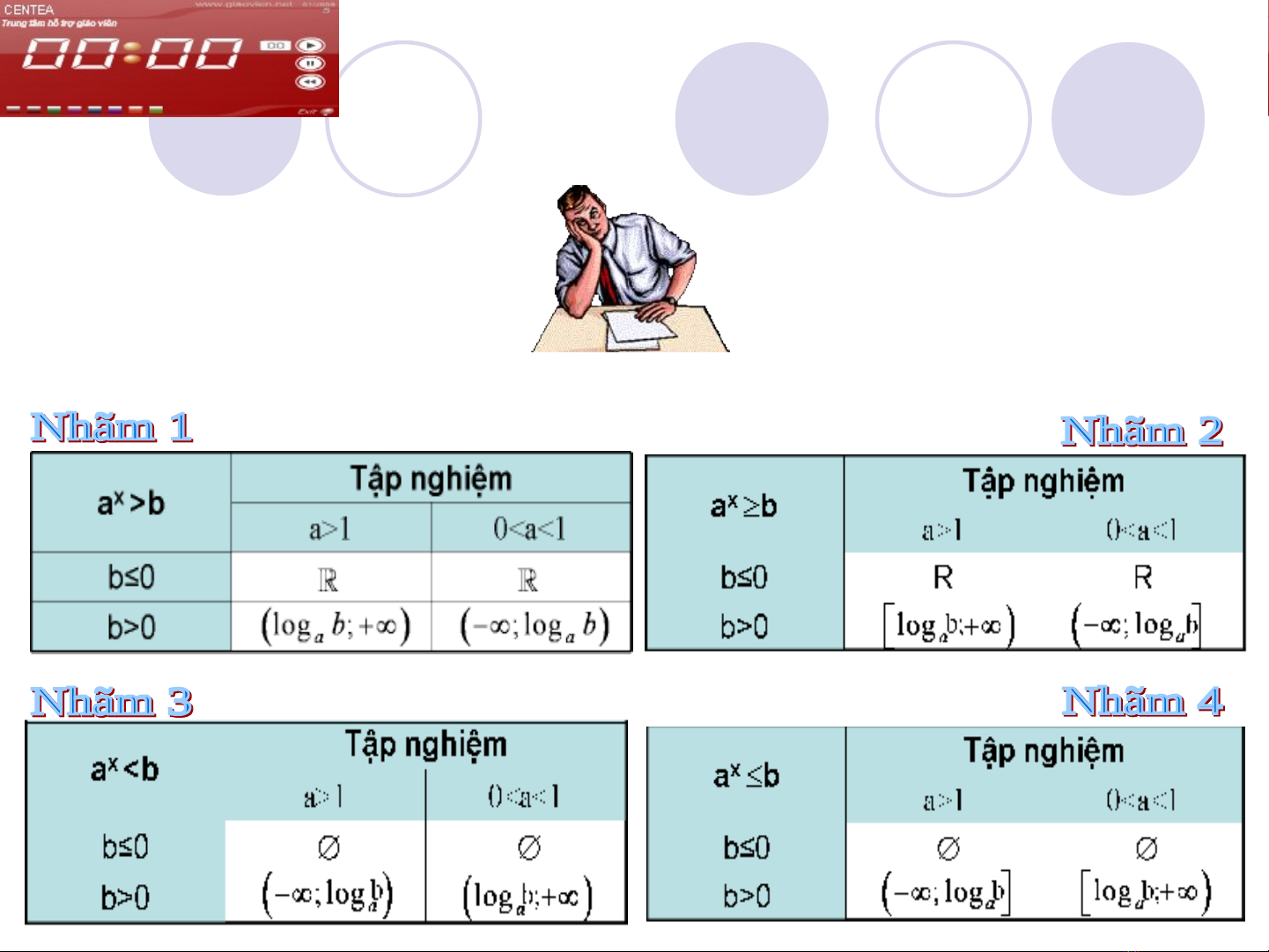
Hãy nêu b ng tóm t t v t p nghi m c a các b t ph ng trình mũ c ả ắ ề ậ ệ ủ ấ ươ ơ
b n:ả
Nhóm 1 : Bpt
Nhóm 2 : Bpt
Nhóm 3 : Bpt
Nhóm 4 : Bpt
x
a b
x
a b
>
x
a b
x
a b
<
K t qu :ế ả
T ph ng trình lôgarit c b n:ừ ươ ơ ả
log
a
x b>
log
( 0; 1)
a
x b
a a
=
>
Khi thay d uấ “=” b i các d uở ấ “>”; “<” ; “≥” ; “≤”
ta đ c cácượ b t ph ng trình lôgarit c b nấ ươ ơ ả
II. B T PH NG TRÌNH LÔGARITẤ ƯƠ
1. B t ph ng trình lôgarit c ấ ươ ơ
b nả
Có d ng :ạ
log ; log ; log )
a a a
x b x b x b
<
( 0; 1)a a
>
(ho cặ
v iớ
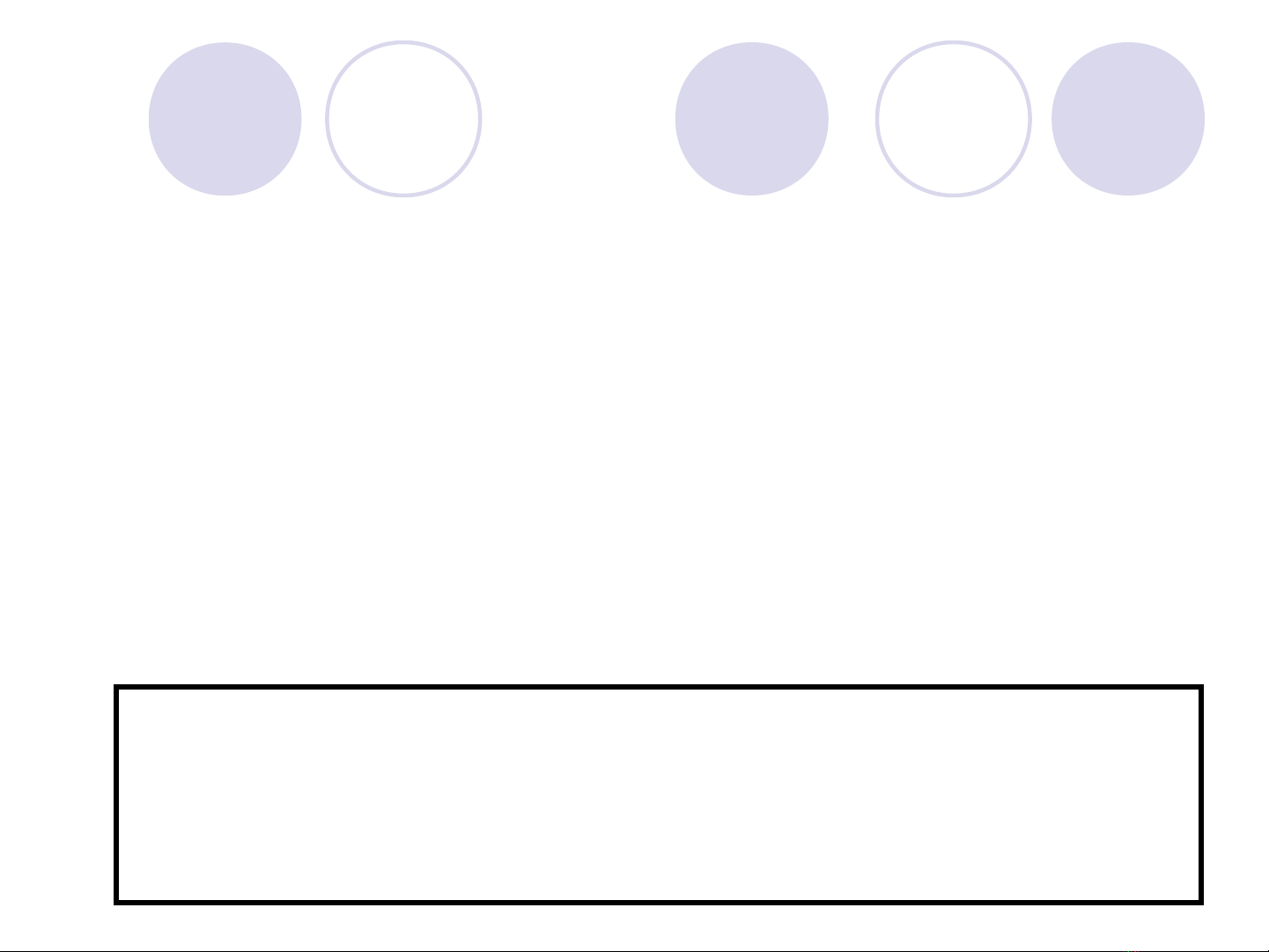
D a vào đ th c a hàm sự ồ ị ủ ố
đ xác đ nh t p nghi m c a các bpt lôgarit c b nể ị ậ ệ ủ ơ ả
log
( 0; 1)
a
y x
a a
=
>
II. B T PH NG TRÌNH LÔGARITẤ ƯƠ
1. B t ph ng trình lôgarit c b nấ ươ ơ ả
Xét b t ph ng trình :ấ ươ
log
( 0; 1)
a
x b
a a
>
>
log
( 1)
a
x b
a
>
>
log
(0 1)
a
x b
a
>
< <
0 1 a
< <
( ; )
b
a
+
B t ph ng trìnhấ ươ
log
a
x b
>
T p nghi mậ ệ
1 a
>
( ; + )
b
a
0 < 1 a
<
( 0 ; )
b
a
II. B T PH NG TRÌNH LÔGARITẤ ƯƠ
1. B t ph ng trình lôgarit c b nấ ươ ơ ả
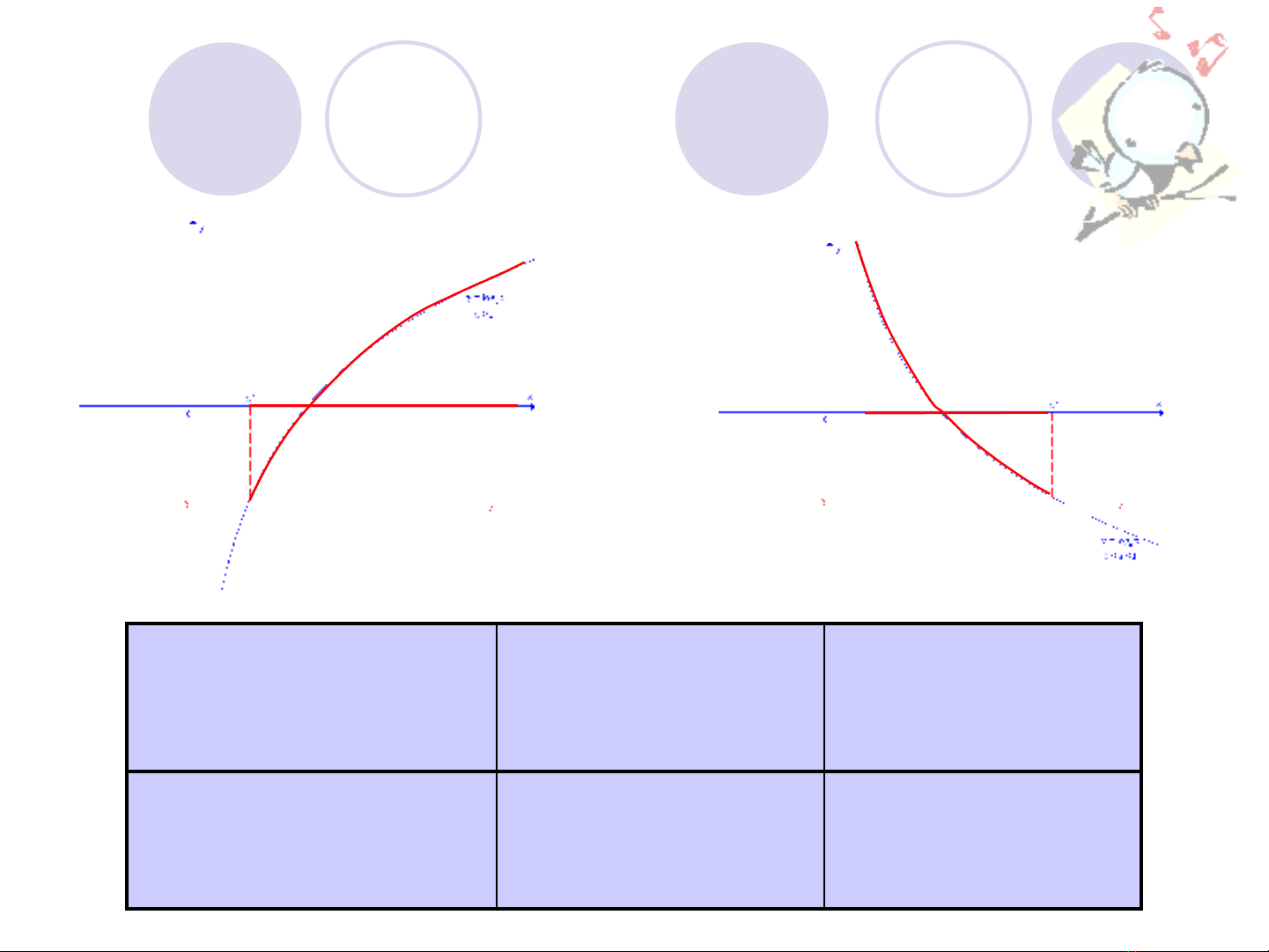
B ng tóm t tả ắ
v t p nghi m c a các b t ph ng trình lôgarit c b nề ậ ệ ủ ấ ươ ơ ả
log
a
x b
>
T p nghi mậ ệ
1a
>
0
b
x a
< <
0 1a
< <
b
x a
>
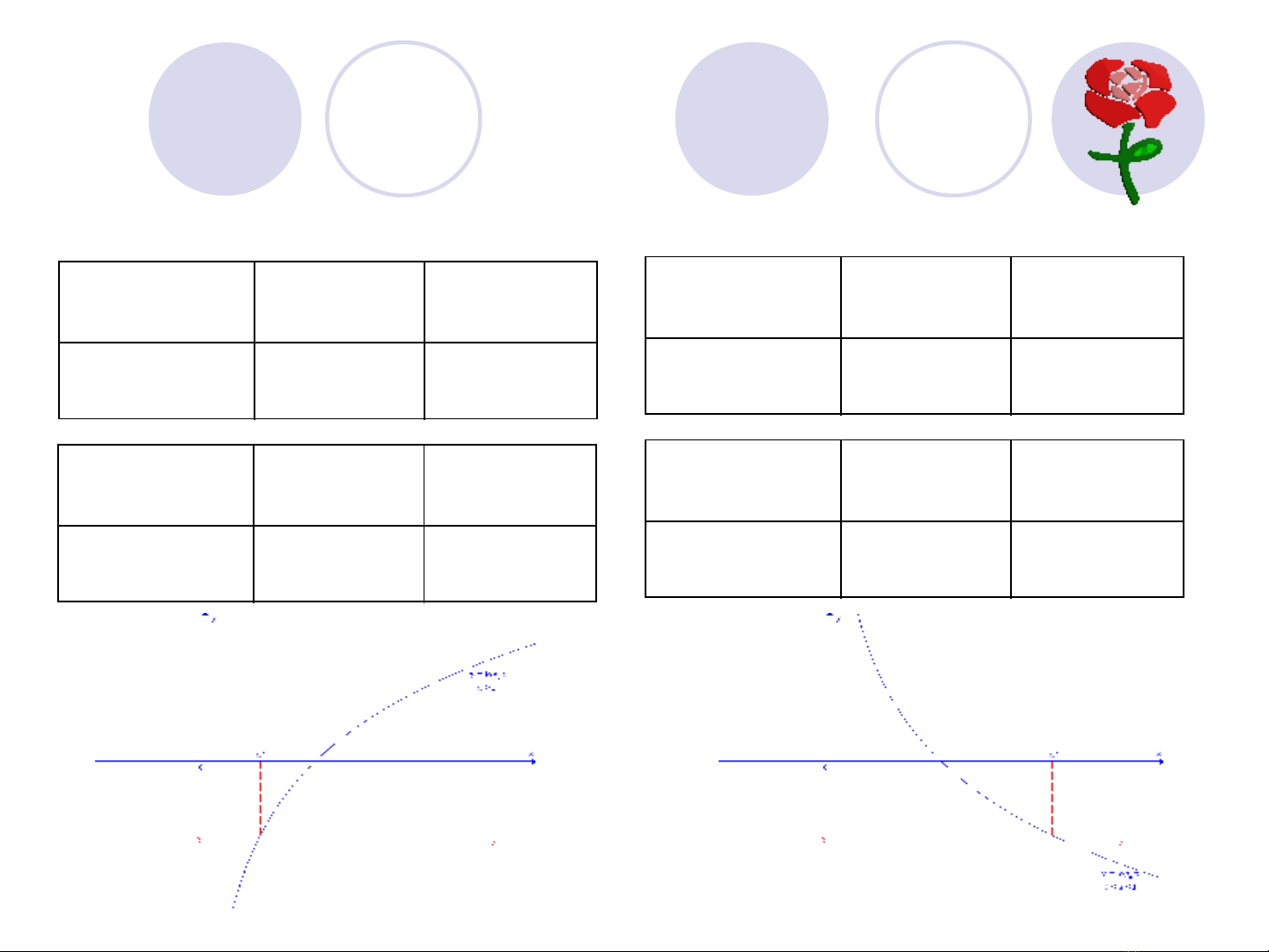
log
a
x b
T p nghi mậ ệ
1a
>
0
b
x a
<
0 1a
< <
b
x a
log
a
x b
<
T p nghi mậ ệ
1a
>
b
x a
>
0 1a
< <
0
b
x a
< <
log
a
x b
T p nghi mậ ệ
1a
>
b
x a
0 1a
< <
0
b
x a
<