CÁC D NG TOÁN Đ I S 10 HK1Ạ Ạ Ố
D ng:Xét tính đ ng bi n,ngh ch bi n c a đ thì hàm s trên (a;b)ạ ồ ế ị ế ủ ồ ố
Ph ng pháp:ươ
B c 1:ướ
Xét x1 <x2 b t kì thu c (a;b).ấ ộ
B c 2: ướ
Ki m tra f(xể1) –f(x2) xem âm hay d ng:ươ
N u f(xế1) –f(x2)<0(t c là f(xứ1) <f(x2))ta k t lu n hàm s y=f(x) đ ng bi n trên (a;b).ế ậ ố ồ ế
N u f(xế1) –f(x2)>0 ta k t lu n hàm s y=f(x) ngh ch bi n trên (a;b).ế ậ ố ị ế
D ng:Xét tính ch n ,l c a hàm s trên t p xác đ nh D c a nóạ ẵ ẻ ủ ố ậ ị ủ
PP
B c 1: ướ
Ki m tra xem TXD D c a hàm s có ph i là m t t p đ i x ng hay khôể ủ ố ả ộ ậ ố ứ ng(T p đ i x ngậ ố ứ
ch là m t trong các d ng R,(a;b), ỉ ộ ạ , , (a>0))
N u TXD D là không ph i là t p đ i x ng thì ta k t lu n hàm s không ch n,không l .ế ả ậ ố ứ ế ậ ố ẵ ẻ
N u D là t p đ i x ng ta làm ti p bế ậ ố ứ ế c 2.ướ
B c 2: ướ
Tính f(-x) và ki m tra xem th :ể ử
+N u f(-x)=f(x) v i m i x thì ta k t lu n hàm s y=f(x) ch n trên D.ế ớ ọ ế ậ ố ẵ
+N u f(-x)=-f(x) v i m i x ta k t lu n hàm s y=f(x) l trên D.ế ớ ọ ế ậ ố ẻ
+Các tr ng h p còn l i ta k t lu n hàm s không ch n cũng không l trên D.ườ ợ ạ ế ậ ố ẵ ẻ
D ng:Ki m tra xem m t đi m M(xạ ể ộ ể M;yM) có thu c đ th hàm s y=f(x) hay khôngộ ồ ị ố
PP:
Thay t a đ đi m M vào công th c c a hàm s :ọ ộ ể ứ ủ ố
N u yếM=f(xM) ta k t lu n đi m M thu c đ th y=f(x).ế ậ ể ộ ồ ị
N u yếM f(xM) ta k t lu n đi m M không thu c đ th y=f(x).ế ậ ể ộ ồ ị
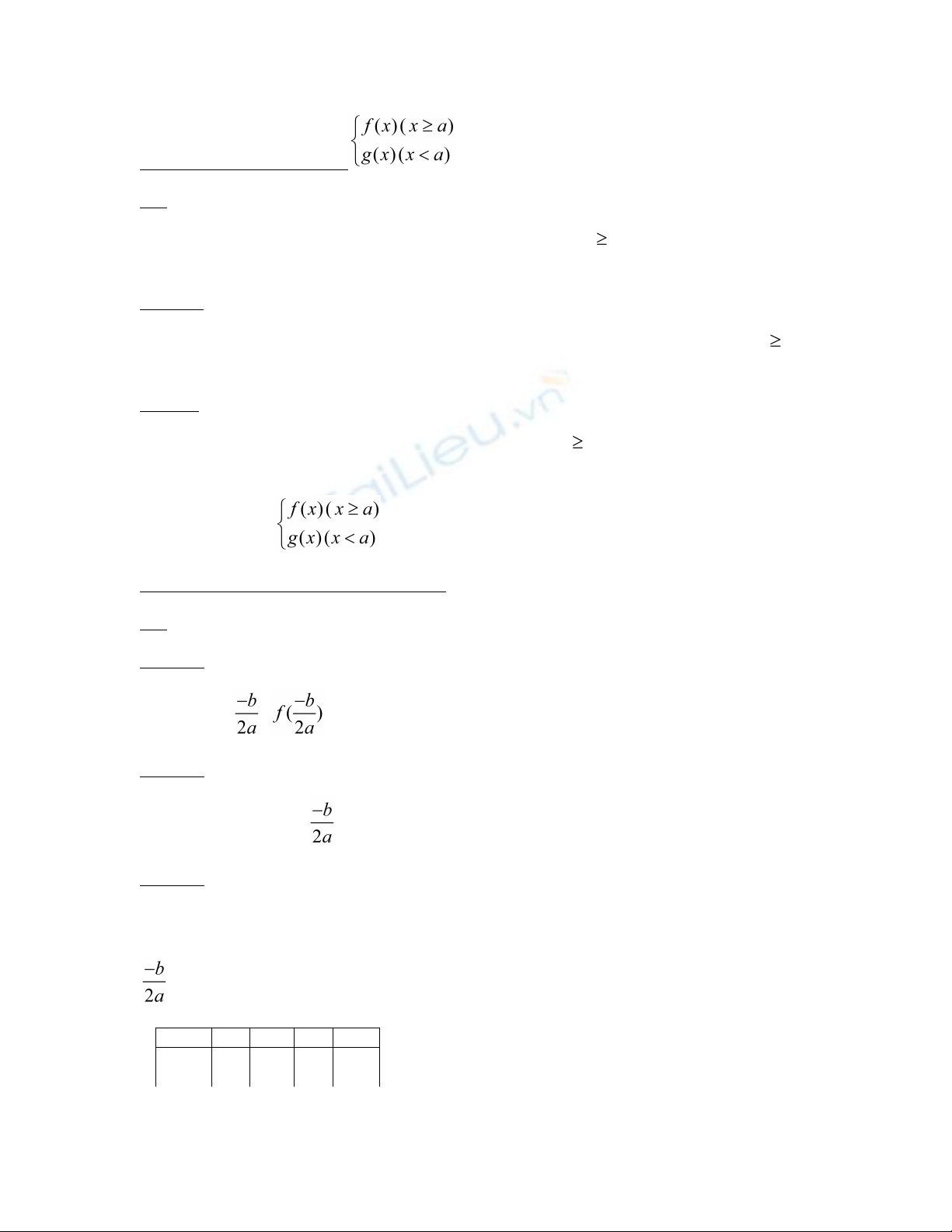
D ng :V đ th hàm s y= ạ ẽ ồ ị ố
PP:
Đ th hàm s trên là m t ph n đ th hàm s y=f(x) v i x ồ ị ố ộ ầ ồ ị ố ớ a và m t ph n đ thộ ầ ồ ị
y=g(x) v i x<a.ớ
B c 1:ướ
V đ th hàm s y=f(x) sau đó b đi ph n đ th mà x<a gi l i ph n đ th mà xẽ ồ ị ố ỏ ầ ồ ị ữ ạ ầ ồ ị a,kí
hi u ph n này là A.ệ ầ
B c 2:ướ
V đ th hàm s y=g(x) sau đó b đi ph n đ th mà xẽ ồ ị ố ỏ ầ ồ ị a gi l i ph n đ th màữ ạ ầ ồ ị
x<a,kí hi u ph n này là B.ệ ầ
Đ th hàm s y= ồ ị ố g m 2 ph n A và B.ồ ầ
D ng: V đ th hàm s y=f(x)=axạ ẽ ồ ị ố 2
+bx+c
PP:
B c 1: ướ
V đ nh I(ẽ ỉ ; ) c a đ th .ủ ồ ị
B c 2: ướ
V tr c đ i x ng x=ẽ ụ ố ứ vuông góc Ox (tr c đ i x ng luôn đi qua đ nh).ụ ố ứ ỉ
B c 3: ướ
L p b ng giá tr đ tìm nh ng đi m mà đ th hàm s đi qua,ph i ghi đi m (0;c) thu cậ ả ị ể ữ ể ồ ị ố ả ể ộ
Ox và đi m (xể1;0) và (x2;0) thu c Oy(n u có) cho d v .Ngoài ra cho nh ng giá tr x cáchộ ế ễ ẽ ữ ị
không quá 2 đ n v .Sau đó v đ th ,chú ý đ c đi m đ i x ng c a đ th .ơ ị ẽ ồ ị ặ ể ố ứ ủ ồ ị
x 0 x1x2m
y=f(x
)
c 0 0 f(m)
D ng: V đ th hàm s y=ạ ẽ ồ ị ố d a vào đ th y=f(x)ự ồ ị
PP:
Đ th y=ồ ị = do đó nó gi ng đ th y=f(x) ph n y ố ồ ị ở ầ 0,còn ở
ph n y<0 thì đ th y=ầ ồ ị đ i x ng v i đ th y=f(x) qua tr c Ox.ố ứ ớ ồ ị ụ
D ng: V đ th hàm s y=f(ạ ẽ ồ ị ố ) d a vào đ th y=f(x)ự ồ ị
PP:
Đ th y=f(ồ ị )= đ i x ng qua Oy(vì hàm s y=f(ố ứ ố ) là hàm s ch n )ố ẵ
và nó gi ng đ th y=f(x) ph n đ th x ố ồ ị ở ầ ồ ị 0,còn ph n đ th x<0 thì đ i x ng v i ph nầ ồ ị ố ứ ớ ầ
đ th x ồ ị 0 qua tr c Oy.ụ
Dạ ng: Tìm GTLN và GTNN c a hàm s y=f(x) trên ủ ố d a vào đ th hàm s đó.ự ồ ị ố
PP:
B c 1 :ướ
Gi i h n ph n đ th đang xét trên [a;b].ớ ạ ầ ồ ị
B c 2:ướ
Xét trên [a;b] đi m nào có v trí cao nh t thì tung đ đi m đó là GTLN c a hàm s trênể ị ấ ộ ể ủ ố
[a;b].
Xét trên [a;b] đi m nào có v trí th p nh t thì tung đ đi m đó là GTNN c a hàm sể ị ấ ấ ộ ể ủ ố
trên [a;b].
D ng: Tìm t a đ giao đi m c a 2 đ th y=f(x) và y=g(x)ạ ọ ộ ể ủ ồ ị
PP:
B c 1 :ướ
T a đ giao đi m c a 2 đ th là nghi m c a hpt: ọ ộ ể ủ ồ ị ệ ủ
Suy ra f(x)=g(x) (*) ,ph ng trươ ình này g i là phọng trươ ình hoành đ giao đi m c a 2 độ ể ủ ồ
th y=f(x) và y=g(x).ị
B c 2:ướ
Gi i (*) suy ra hoành đ giao đi m,sau đó th vào m t trong 2 pt y=f(x) ho c y=g(x) thìả ộ ể ế ộ ặ
tìm đ c tung đ giao đi m.ượ ộ ể
D ng : Tìm s nghi m c aạ ố ệ ủ pt f(x)=m tùy theo giá tr c a m.ị ủ
PP:
B c 1: ướ
Ph ng trươ ình trên là pt hoành đ giao đi m c a 2 đ th y=f(x) và y=m,vì v y n u 2 độ ể ủ ồ ị ậ ế ồ
th này c t nhau bao nhiêu đi m thì pt có b y nhiêu nghi m.ị ắ ở ể ấ ệ
B c 2: ướ
D a vào đ th hay b ng bi n thiên c a hàự ồ ị ả ế ủ m s y=f(x) ta suy ra đ c s đi m c t.ố ượ ố ể ắ
D ng: Tìm công th c hàm s y=ax+b, t c tìm a và bạ ứ ố ứ
Ki n th c h tr :ế ứ ỗ ợ
Hai đ ng th ng y=ax+b và y=cx+d song song ườ ẳ a=c.
Hai đ ng th ng y=ax+b và y=cx+d vuông góc ườ ẳ a.c=-1
Ph ng pháp:ươ
D a vào gi thi t bài toán ta tìm 2 bi u th c có s liên quan tr c ti p gi a a và b,sauự ả ế ể ứ ự ự ế ữ
đó gi i hpt b c nh t 2 n a và b s tìm đ c a,b.Sau đó ghi công th c hàm s th a yêuả ậ ấ ẩ ẽ ượ ứ ố ỏ
c u bài toán( ycbt).ầ
D ng: Tìm công th c hàm s y=axạ ứ ố 2
+bx+c
Ph ng pháp:ươ
+N u đ bài cho m t trong 3 h s a,b,c thì ta tìm 2 h s còn l i b ng cách tìm h 2ế ề ộ ệ ố ệ ố ạ ằ ệ
pt b c nh t 2 n.ậ ấ ẩ
+N u đ bài không cho m t trong 3 h s a,b,c thì ta d a vào gi thi t bài toán tìm 3ế ề ộ ệ ố ự ả ế
pt cho th y s liên quan gi a a,b,c sau đó l p hpt b c 1 ba n a,b,c r i gi i h tìm đ cấ ự ữ ậ ậ ẩ ồ ả ệ ượ
a,b,c.Sau đó ta vi t công th c hàm s th a ycbt.ế ứ ố ỏ
D ng: Gi i pt ạ ả =g(x)
PP:
B c 1: ướ
Đ t đi u ki n và gi i bpt g(x) ặ ề ệ ả 0
B c 2:ướ
Pt
Gi i pt (1) tìm đ c nghi m r i đ i chi u v i đk.ả ượ ệ ồ ố ế ớ
Gi i pt (2) tìm đ c nghi m r i đ i chi u v i đk.ả ượ ệ ồ ố ế ớ
Sau đó k t lu n nghi m c a pt.ế ậ ệ ủ
D ng : Gi i ptạ ả
PP:
Pt
Gi i pt (1) và pt(2) và t ng h p nghi m c a pt ban đ u mà không có đi u ki n gì c .ả ổ ợ ệ ủ ầ ề ệ ả
D ng: Gi i pt ạ ả
PP:
B c 1: ướ
Đ t đk g(x) ặ0 và gi i đi u ki n(Đk f(x) ả ề ệ 0 là th a).ừ
B c 2:ướ
Pt f(x)=g2(x) (Bình ph ng 2 v ươ ế 0)
Gi i nghi m pt này r i đ i chi u v i đk.ả ệ ồ ố ế ớ
D ng: Ch ng minh b t đ ng th c(BĐT)ạ ứ ấ ẳ ứ
Công c h tr :ụ ỗ ợ
BĐT Cauchy cho 2 s không âm x và y và các d ng khác nhau c a nó: x+y ố ạ ủ .
f(x) g(x) f(x) +h(x) g(x) +h(x) (c ng c 2 v cùng m t lộ ả ế ộ ng b ng nhau thượ ằ ì BĐT
không đ i chi u)ổ ề
f(x) g(x) f(x).h(x) g(x).h(x) ( h(x) 0) (Nhân c 2 v BĐT cho cùng m t bi uả ế ộ ể
th c dứng thươ ì BĐT không đ i chi u ).ổ ề