GII ðÁP TOÁN CP 3 – THI ðI HC
CÁC BÀI TOÁN TRONG
TAM GIÁC, T GIÁC
CÁC BÀI TOÁN V
ðƯNG THNG
CÁC BÀI TOÁN V
ðƯNG TRÒN
CÁC BÀI TOÁN V ELIP
CÁC HƯNG TƯ DUY VÀ PHƯƠNG PHÁP GII
TRONG HÌNH HC OXY
Biên son: Thanh Tùng
*) Tóm tt lý thuyt ñy ñ theo mt trình t logic và có h thng.
*) ðưa ra các hưng tư duy và phương pháp gii khái quát cho tng lp bài toán.
*) Có bài toán mu minh ha ñi kèm.
*) Phn bài tp áp dng có gi ý.
*) Li gii chi tit cho tng bài toán c th
(tham kho thêm trên http://www.facebook.com/giaidaptoancap3 ).
BÀI TOÁN TÌM ðI M
H À N!I 0 3 / 2 0 1 3
2
CÁC HƯNG TƯ DUY VÀ PHƯƠNG PHÁP GII HÌNH HC OXY
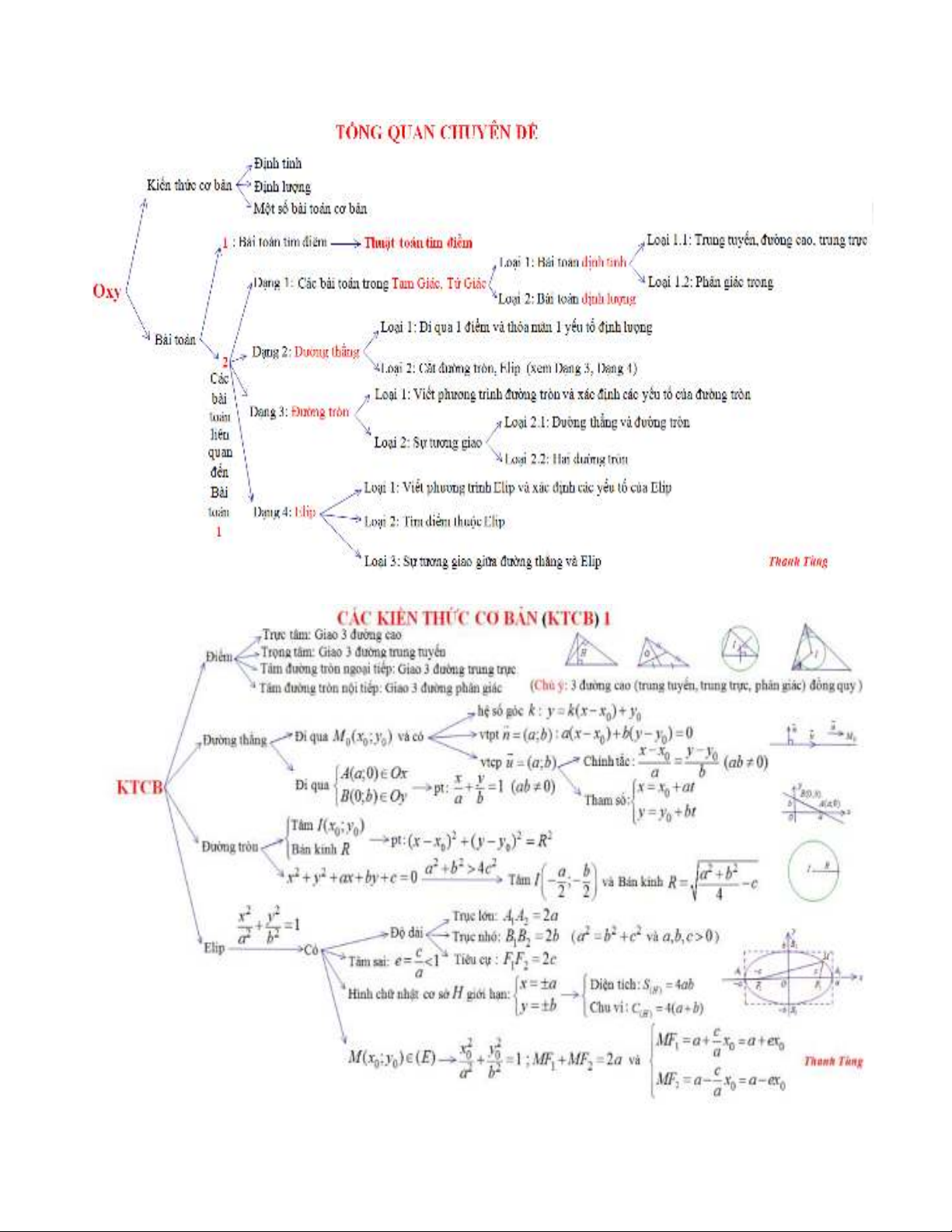
A. KIN THC CƠ BN
3
4
B. CÁC BÀI TOÁN
BÀI TOÁN 1: BÀI TOÁN TÌM ðIM
ð hiu rõ hơn cho 4 hưng tư duy tương ng vi 4 TH ca Bài toán 1: “Bài Toán Tìm ðim” thy s
dùng 6 bài thi ði Hc năm 2012 va qua ñ minh ha.
1) (A, A1 – 2012:CB). Cho hình vuông ABCD. Gi M là trung ñim ca cnh BC, N là ñim trên cnh CD sao cho
CN = 2ND. Gi s
11 1
;
2 2
M
và ñưng thng AN có phương trình
2 3 0
x y
− − =
. Tìm ta ñ ñim A.
2) (A, A1 – 2012 :NC). Cho ñưng tròn 2 2
( ) : 8
C x y
. Vit phương trình chính tc ca elip (E), bit rng (E) có
ñ dài trc ln bng 8 và (E) ct
( )
C
ti bn ñim phân bit to thành bn ñnh ca mt hình vuông.
3) (B – 2012:CB). Cho ñưng tròn 2 2
1
( ) : 4
C x y
+ =
,2 2
2
( ) : 12 18 0
C x y x
+ − + =
và ñưng thng
: 4 0
d x y
− − =
.
Vit phương trình ñưng tròn có tâm thuc
2
( )
C
, tip xúc vi d và ct
1
( )
C
ti hai ñim phân bit A và B sao cho AB
vuông góc vi d.
4) (B – 2012 :NC). Cho hình thoi ABCD có AC = 2BD và ñưng tròn tip xúc vi các cnh ca hình thoi có phương
trình 2 2
4
x y
+ =
. Vit phương trình chính tc ca elip (E) ñi qua các ñnh A, B, C, D ca hình thoi. Bit A thuc Ox.
5) (D – 2012:CB). Cho hình ch nht ABCD. Các ñưng thng AC và AD ln lưt có phương trình là
3 0
x y
+ =
và
4 0
x y
−+=
; ñưng thng BD ñi qua ñim
1
( ;1)
3
M−. Tìm ta ñ các ñnh ca hình ch nht ABCD.
6) (D – 2012 :NC). Cho ñưng thng
: 2 3 0
d x y
− + =
. Vit phương trình ñưng tròn có tâm thuc
d
, ct trc Ox
ti A và B, ct trc Oy ti C và D sao cho AB = CD = 2.
5
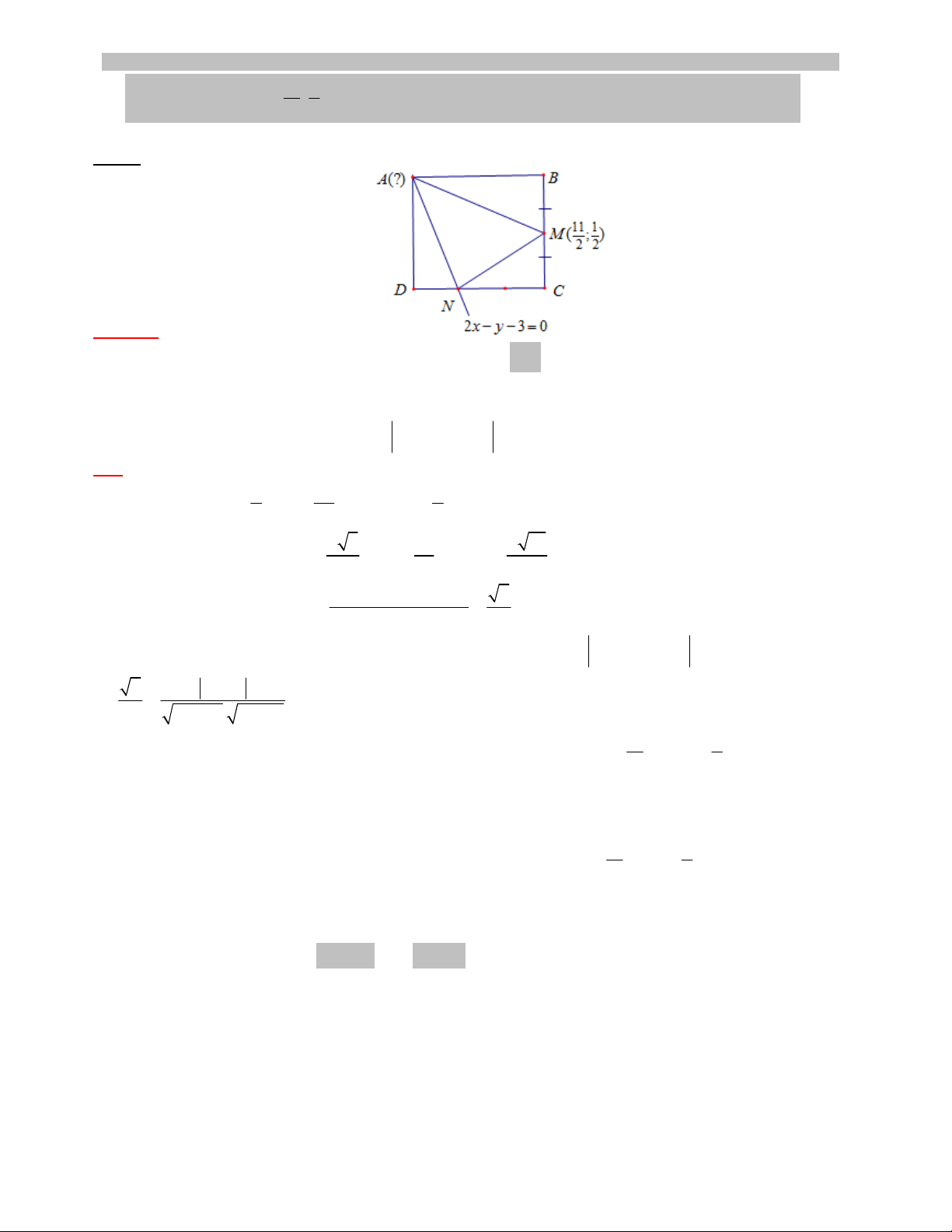
1) (A, A1 – 2012:CB). Cho hình vuông ABCD. Gi M là trung ñim ca cnh BC, N là ñim trên cnh CD sao cho
CN = 2ND. Gi s
11 1
;
2 2
M
và ñưng thng AN có phương trình
2 3 0
x y
− − =
. Tìm ta ñ ñim A.
Cách 1
Phân tích: :
+) Ta có
{
}
A AN AM
= ∩ nên Theo hưng tư duy 1 (TH1) ta phi ñi lp thêm phương trình
AM
+) Bit
M
nhưng chưa bit
A
(chính là ñáp s ta cn tìm) nên ta phi ñi tìm thêm vtpt hoc vtcp
+) Bài toán không có yu t song song, vuông góc ñ tìm vtpt hoc vtcp nên ta phi khai thác yt ñnh lưng
+) Yu t ñnh lưng: cos
MAN
∠
=
(
)
cos ,
AM AN
n n
AM
n
⇒
⇒
phương trình AM
→
ta ñ ñim
A
Gii:
ðt
AB a
=
2
; ;
3 3 2
a a a
ND NC MB MC
⇒= = = =
( vì
ABCD
là hình vuông và 2
CN ND
=
)
Và áp dng Pitago ta ñưc:
5 5
;
2 6
a a
AM MN= = và
10
3
a
AN =
Trong
AMN
∆
ta có: cos
MAN
∠
2 2 2
2
2 . 2
AM AN MN
AM AN
+ −
= =
Gi
( ; )
AM
n a b
=
là vtpt ca
AM
và ta có
(2; 1)
AN
n
= −
cos
⇒
MAN
∠
=
(
)
cos ,
AM AN
n n
2 2 2 2 2
2 2 2 2
3
2
22(2 ) 5( ) 3 8 3 0 (3 )( 3 ) 0
3
2. 2 1
a b
a b a b a b a ab b a b a b
a b
a b
= −
−
⇔ = ⇔ − = + ⇔ − − = ⇔ + − = ⇔ =
+ +
+) Vi 3
a b
= −
chn
1; 3
a b
= = −
(1; 3)
AM
n
⇒= −
⇒
phương trình 11 1
: 3 0
2 2
AM x y
− − − =
hay
: 3 4 0
AM x y
− − =
. Vì
{
}
A AN AM
= ∩ nên ta gii h: 2 3 0 1
(1; 1)
3 4 0 1
x y x A
x y y
− − = =
⇔⇒−
− − = = −
+) Vi
3
a b
=
chn
3; 1
a b
= =
(3;1)
AM
n⇒=
⇒
phương trình 11 1
:3 0
2 2
AM x y
− + − =
hay
:3 17 0
AM x y
+ − =
. Vì
{
}
A AN AM
= ∩ nên ta gii h: 2 3 0 4
(4;5)
3 17 0 5
x y x A
x y y
− − = =
⇔⇒
+ − = =
Vy
(1; 1)
A
−
hoc
(4;5)
A