2
CÁC HƯNG TƯ DUY VÀ PHƯƠNG PHÁP GII HÌNH HC OXY
A. KI N THC CƠ BN
http://megabook.vn/
3
http://megabook.vn/
4
B. CÁC BÀI TOÁN
BÀI TOÁN 1: BÀI TOÁN TÌM ðIM
ð hiu rõ h ơn c h o 4 h ưng tư d u y t ư ơ ng ng vi 4 TH ca Bà i t o án 1 : “ Bà i T o án T ìm ðim” thy s
dùng 6 bài thi ði H c năm 2012 va qua ñ minh ha.
1) (A, A1 – 2012:CB). Cho hình vuông ABCD. Gi M là trung ñim c a c nh BC, N là ñi m trên cnh CD sao cho
CN = 2ND. Gi s
11 1
;
2 2
M
và ñưng thng AN có phương trình
2 3 0
x y
− − =
. Tìm ta ñ ñim A.
2) (A, A1 – 2012 :NC). Cho ñưng tròn 2 2
( ) : 8
C x y
+ =
. Vi t phươn g t r ì nh ch í n h t c c a e l i p ( E), bit rng (E) có
ñ dài trc ln b ng 8 và (E) ct
( )C
ti bn ñ i m phân bit to thành bn ñ nh ca mt hình vuông.
3) (B – 2012:CB). Cho ñưng tròn 2 2
1
C x y
+ =
, 2 2
2
( ) : 12 18 0
C x y x
+ − + =
và ñưng thng
: 4 0
d x y
− − =
.
Vi t phương trình ñưng tròn có tâm thuc
2
( )
C
, ti p xúc vi d và ct
1
( )
C
ti hai ñim phân bi t A và B sao cho AB
vu ô n g g ó c v i d.
4) (B – 2012 :NC). Cho hình thoi ABCD có AC = 2BD và ñưng tròn ti p xúc vi các cnh ca h ì n h t h o i c ó p h ương
trình 2 2
4
x y
+ =
. Vit phương trình chính tc ca elip (E) ñi qua các ñnh A, B, C, D ca hình thoi. Bi t A thuc Ox.
5) (D – 2012:CB). Cho hình ch nht ABCD. Các ñưng th ng AC và AD ln lưt có phương trình là
3 0
x y
+ =
và
4 0
x y
− + =
; ñưng thng BD ñi qua ñim
1
( ;1)
3
M − . Tìm ta ñ các ñnh ca hình ch nht ABCD.
6) (D – 2012 :NC). Cho ñưng th ng
: 2 3 0
d x y
− + =
. Vit phương trình ñưng tròn có tâm thuc
d
, c t trc Ox
ti A và B, ct trc Oy t i C và D sao cho AB = CD = 2.
http://megabook.vn/
5
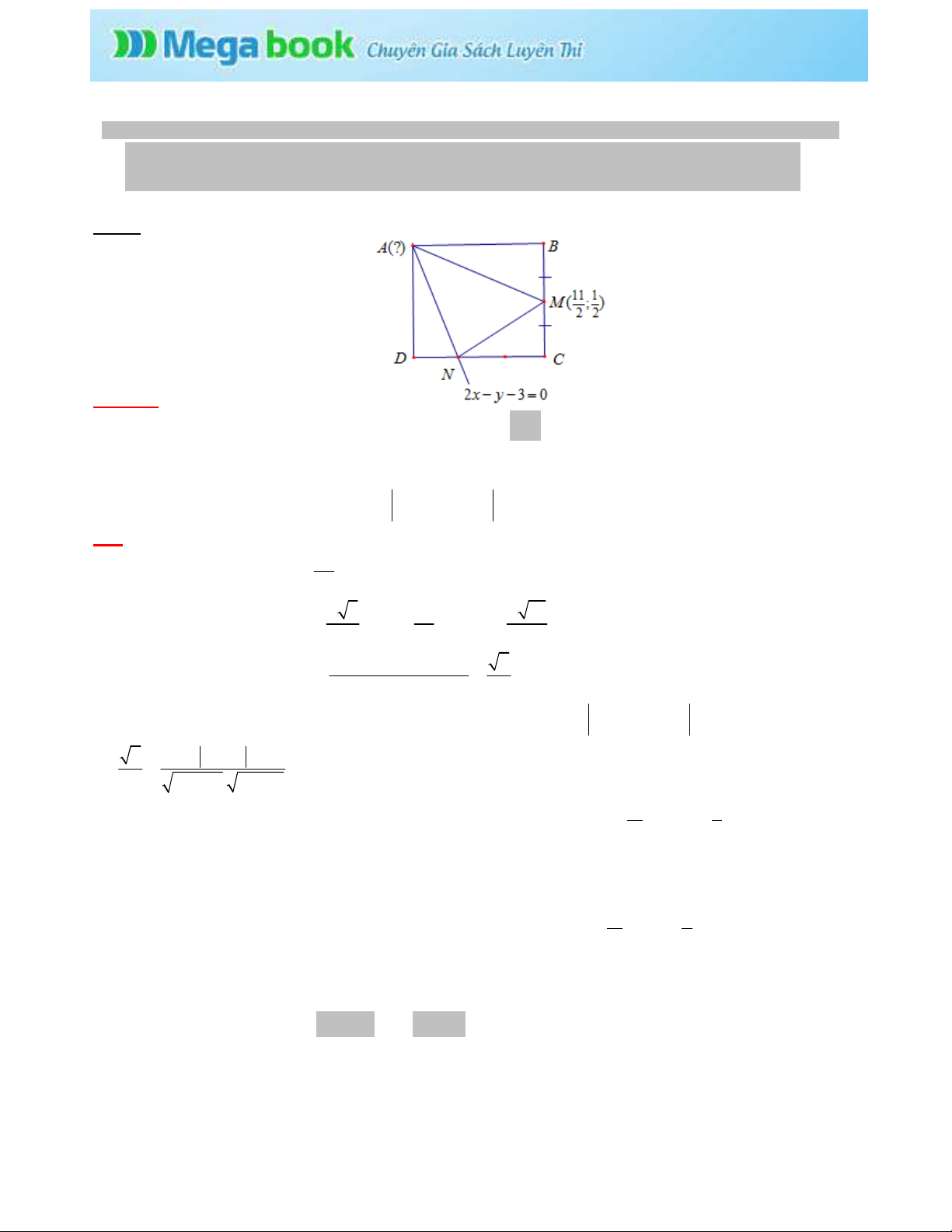
1 ) (A, A1 – 2012:CB). Cho hình vuông ABCD. Gi M là trung ñim ca c nh BC, N là ñi m trên cnh CD sao cho
CN = 2ND. Gi s
11 1
;
2 2
M
và ñưng th ng AN có phương trình
2 3 0
x y
− − =
. Tìm ta ñ ñ i m A.
Cách 1
Phân tích: :
+) Ta có
{
}
A AN AM
= ∩ nên Theo hưng tư duy 1 (TH1) ta ph i ñi lp thêm phương trình
AM
+) Bi t
M
nhưng chưa b i t
A
(chính là ñáp s ta c n tìm) nên ta phi ñi tìm thêm vtpt ho c vtcp
+) Bài toán không có y u t song song, vuông góc ñ tìm vtpt hoc vtcp nên ta ph i khai thác yt ñnh lưng
+) Yu t ñ nh lưng: cos
MAN
∠
=
(
)
cos ,
AM AN
n n
A M
n
⇒
⇒
phương trình A M
→
t a ñ ñim
A
Gii:
ðt
A B a=
2
; ;
3 3 2
a a a
ND NC MB MC
⇒= = = =
( vì
ABC D
là hình vuông và 2
C N N D=
)
Và áp dng Pitago ta ñưc:
5 5
;
2 6
a a
AM MN= = và 10
3
a
AN =
Trong
A M N
∆
ta có: cos
MAN
∠
2 2 2
2
2 . 2
AM AN MN
AM AN
+ −
= =
Gi
( ; )
AM
n a b
=
là vtpt ca
AM
và ta có
(2; 1)
AN
n
= −
cos
⇒
MAN
∠
=
(
)
cos ,
AM AN
n n
2 2 2 2 2
2 2 2 2
3
2
2 2(2 ) 5 ( ) 3 8 3 0 (3 )( 3 ) 0
3
2 . 2 1
a b
a b a b a b a ab b a b a b
a b
a b
= −
−
⇔ = ⇔ − = + ⇔ − − = ⇔ + − = ⇔ =
+ +
+) Vi 3
a b
= −
chn
1 ; 3
a b
= = −
( 1 ; 3 )
AM
n
⇒= −
⇒
phương trình 11 1
: 3 0
2 2
AM x y
− − − =
hay
: 3 4 0
AM x y
− − =
. Vì
{
}
A AN AM
= ∩ nên ta gii h: 2 3 0 1
( 1 ; 1 )
3 4 0 1
x y x A
x y y
− − = =
⇔ ⇒−
− − = = −
+) Vi
3
a b
=
chn
3 ; 1
a b
= =
(3;1)
AM
n⇒=
⇒
phương trình 11 1
:3 0
2 2
AM x y
− + − =
hay
:3 17 0
AM x y
+ − =
. Vì
{
}
A AN AM
= ∩ nên ta gi i h : 2 3 0 4
(4;5)
3 17 0 5
x y x A
x y y
− − = =
⇔ ⇒
+ − = =
Vy
( 1 ; 1 )
A
−
ho c
(4;5)
A
http://megabook.vn/
6
Cách 2:
Phân tích:
A AN∈
nên Theo hưng tư duy 2 (TH2) ta gi ( )
A t AN
∈
ta cn thit lp 1 phương trình
( ) 0
f t
=
(còn d kin
11 1
;
2 2
M
là trung ñim ca
B C
ta chưa s dng – s giúp ta làm ñiu này) ?
t
→ = →
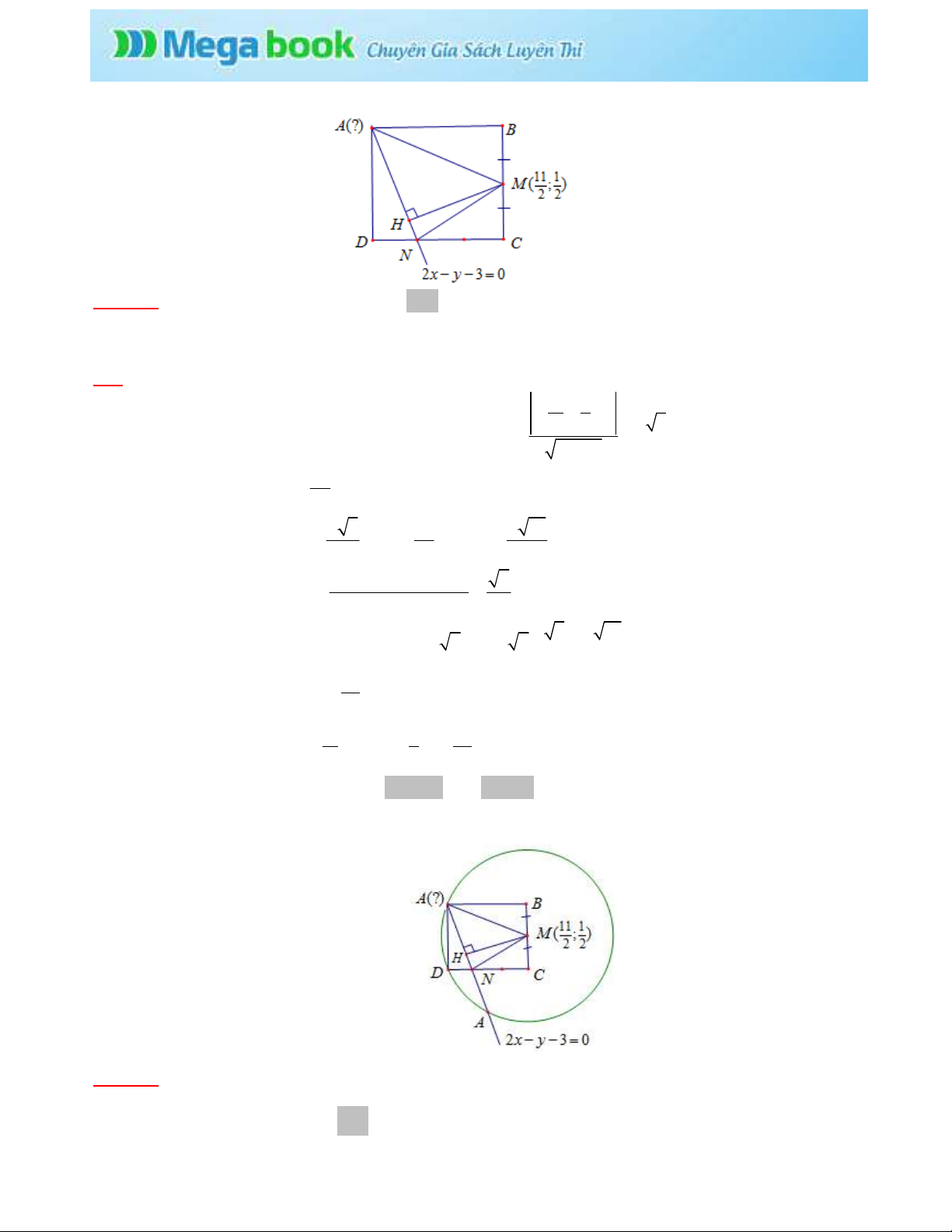
Gii:
+) Gi
H
là hình chi u ca
M
lên
A N
2 2
11 1
2. 3
3 5
2 2
( , )
2
2 1
MH d M AN
− −
⇒= = =
+
ðt
A B a=
2
; ;
3 3 2
a a a
ND NC MB MC
⇒= = = =
( vì
A B C D
là hình vuông và 2
C N N D=
)
Và áp dng Pitago ta ñưc:
5 5
;
2 6
a a
AM MN= = và 10
3
a
AN =
Trong
A M N
∆
ta có: cos
MAN
∠
2 2 2
2
2 . 2
AM AN MN
AM AN
+ −
= =
⇒
MAN
∠
=
0
45
M A H
⇒∆
cn ti
H
3 5 3 10
2 2.
2 2
AM MH⇒= = = (*)
+) Gi ( ;2 3 )
A t t AN
− ∈
và 245
2
AM = (theo (*))
⇔
2 2
2
1 ( 1 ; 1 )
11 7 45
2 5 4 0
4 (4;5)
2 2 2
t A
t t t t t A
= −
− + − = ⇔ − + = ⇔ ⇒
=
V y
( 1 ; 1 )
A
−
hoc
(4;5)
A
Cách 3:
Phân tích:
A AN∈
và
11 1
;
2 2
M
c ñnh . Nu
A M h c o n s t= =
( ta s tìm cách ñi tính
AM
).
Nên Theo hưng tư duy 3 (TH3) :
{
}
( )
A A N C
= ∩ vi
( )C
là ñưng tròn tâm
M
bán kính
R h=
http://megabook.vn/