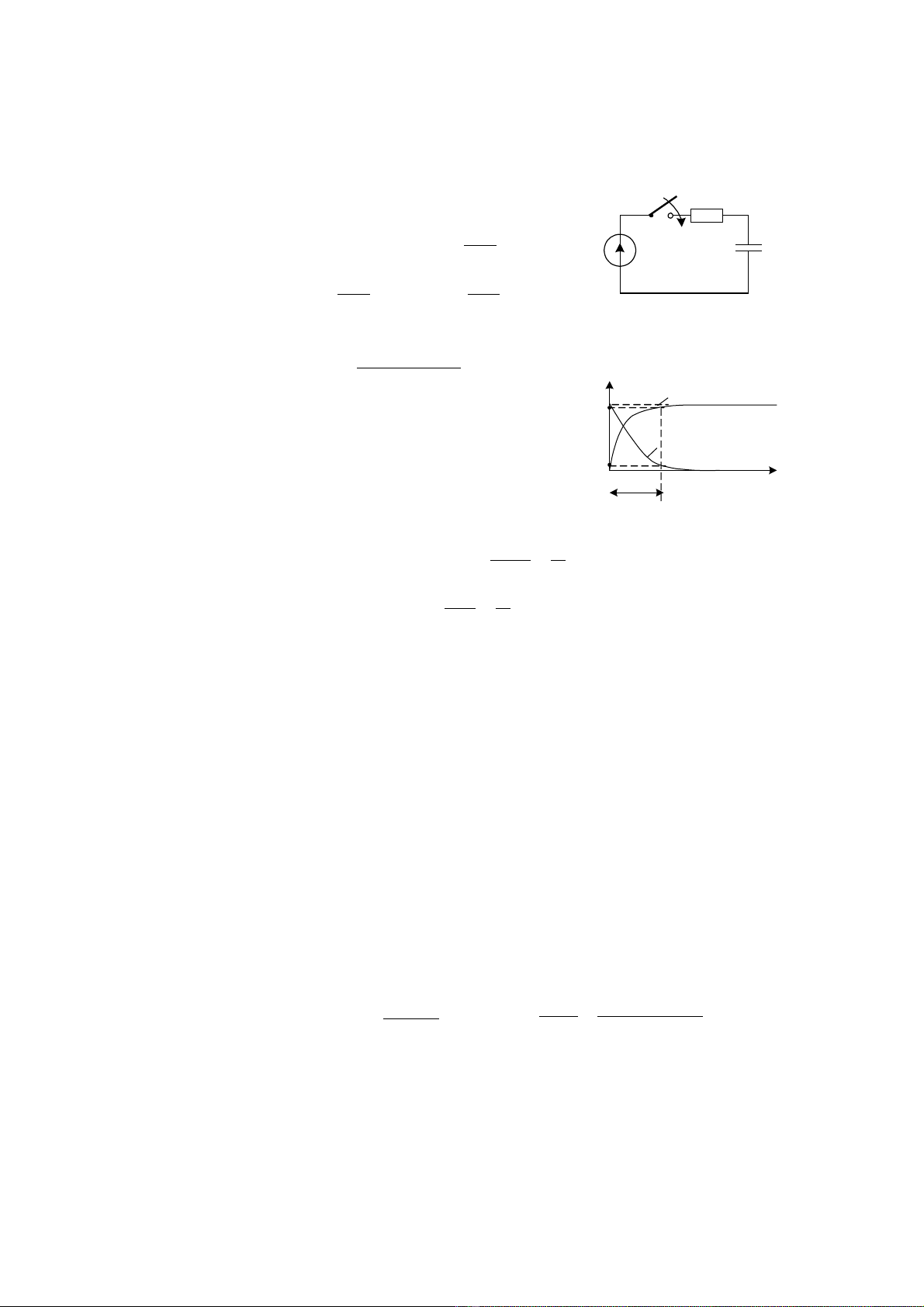
L i Gi i - đáp s - ch d nờ ả ố ỉ ẫ
3.1. Hình 3.48.
1. a) Ph ng trình đ nh lu t Kiêckhop 2:ươ ị ậ
uR+uC=E. Ch n bi n s là uọ ế ố C thì i=
dt
du
CC
.
T đó có R. i+uừC=R
dt
du
CC
+uC=E hay
dt
duC
+αuC=αE
Trong đó α=1/RC=1/τ=
10
1020105
1
63 =
−
...
[1/s]
Nghi m là: ệ
ttt
t
t
dtdt
C
C eE]eEC[e
]dteEC[e]dteEC[eu
α−αα−
α
α−
αα−
+=+=
α+=
∫
α+
∫
=∫∫
.
Vì uC(0)=E+C=0 (đây là đi u ki n ban đ u) nênề ệ ầ
C=-E→ uC(t)=E(1-e-αt)=100(1-e-10t)
T đó uừR(t)=E-uC(t)=Ee-αt=100e-10t; i(t)=
t
Re
R
E
R
)t(u α−
=
=0,02e-10t hay tính
i(t)=
t
Ce
R
E
dt
du
Cα−
=
=0,02e-10t[A]
Đ th các đ i l ng hình 3.49. ồ ị ạ ượ
b) Theo công th c 3.7. thì uứC(t)=Ae-αt +B
H s ệ ố α theo (3.8) thì α=1/RtđC=1/RC=10[1/s] vì Rtđ=R (khi đã đóng khoá K
và cho ngu n tác đ ng b ng 0). Khi tồ ộ ằ →∞ thì uC(∞)=B=E vì lúc đó m ch chạ ở ế
đ m t chi u khi C n p đ y đ n đi n áp b ng E. Khi t=0 thìộ ộ ề ạ ầ ế ệ ằ
uC(0)=A+B=A+E=0 nên A=-E và uC(t)=E(1-e-αt)= 100(1-e-10t)
2. N u không m c R thì t i t=0 có uế ắ ạ C(0)=0 nên ngu n b ch p qua t C gâyồ ị ậ ụ
h ng ngu n.ỏ ồ
3.2. i(t)=0,5(1-e-200t) [A];uL(t)=50e-100t [V] ; uR(t)=50(1-e-100t). [V]
3.3. R1=10 Ω ; L1=0,2H ; R2=20Ω ; L2=0,1H
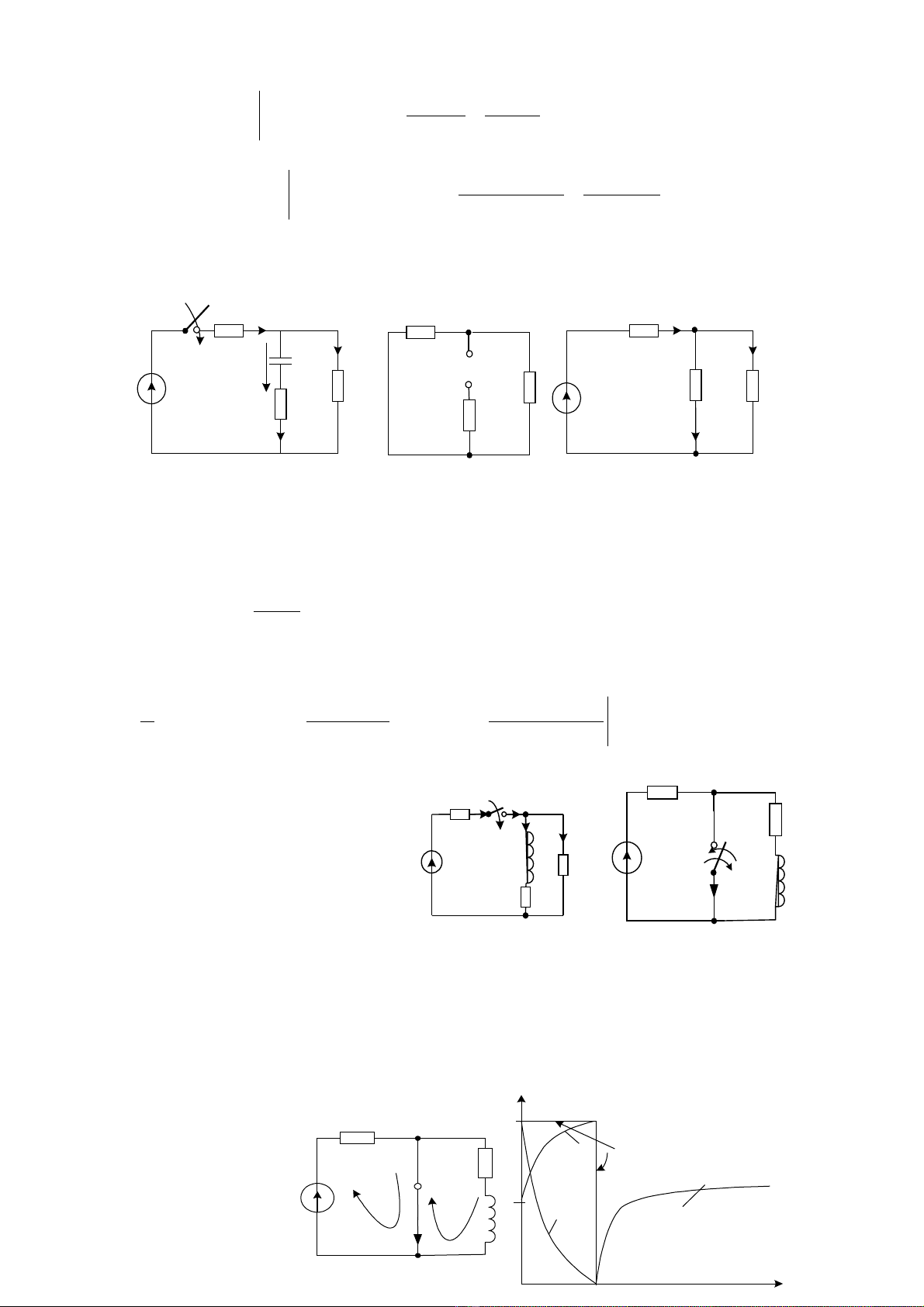
3.4. T m ch hình 3.50 a) ng t b C, nhìn t 2 đi m v a c t vào m ch khiừ ạ ắ ỏ ừ ể ừ ắ ạ
cho ngu n tác đ ng b ng 0 s có m ch hình 3.50b).T đó có:ồ ộ ằ ẽ ạ ừ
Ω=
+
+=+= 30
3020
3020
18
312
.
)R//R(RR td
;
500
10676630
11
6≈==α −
.,.
CR td
[1/s]
Đ u tiên tính dòng iầ1(t)=Ae-500t+B;
t
i(t)
0
H×nh 3.49
R
C
u (t)
u (t)
E
t
XL
0,95E
0,05E
97
i1(
1
3020
50
31
=
+
=
+
==∞=
∞→ RR
E
B)(i
t
)t
, vì khi đó m ch ch đạ ở ế ộ
m t chi u xác l p, không có dòng m t chi u qua C.ộ ề ậ ộ ề
61
251120
50
0
0321
11 ,
,R//RR
E
BA)(i
t
)t(i =
+
=
+
=+==
=
, vì khi t=0
thì uC(0)=0 nên C thay b ng dây d n (hình 3.50c).ằ ẫ
A=1,6-B=0,6 nên i1(t)=0,6e-500t+1 [A]
Các dòng khác có th tính t ng t , tuy nhiên nên áp d ng các đ nhể ươ ự ụ ị
lu t c b n đ tính qua iậ ơ ả ể 1(t) s nhanh h n:ẽ ơ
uR1(t)=R1i1(t)=12e-500t+20[V]; uR3(t)=E-uR1(t)=-12e-500t+30[V]
]A[e,
R
)t(u
)t(i
t
R
R
140
500
3
3
3
+−==
−
; iR2(t)=iR1(t)-iR3(t)=e-500t.[A]
]V[)e(e)t(iR)t(u)t(u tt
RC
500500
223 1303030 −− −=−=−=
Có th ki m tra giá tr uể ể ị C(t) theo công th c:ứ
)e(
t
.,.
e
dte
.,
)(udt)t(i
C
t
t
t
t
t
CR
500
6
500
0
500
0
6
2
130
0
106766500106766
1
0
1
−
−
−
−
−
−≈−==+
∫∫
[V]
3.5. Hình 3.51
5460 40 ,e,)t(i t+−= −
;
]A[)e(,i
];A[e,,i
t
R
t
R
40
1
40
2
181
2172
−
−
−=
+=
.e,)t(u t
L
40
846 −
=
[V]
3.6. L=0,5H
3.7. Hình 3.52.
Ch a đóng K: ưM ch xác l p v i dòng m t chi u:ạ ậ ớ ộ ề
H×nh 3.50
a)
K
C
R
ERR
1
2
3
i (t)
i (t)
i (t)
u (t)
2
3
1
C
R
RR
1
2
3
R
RR
1
2
i (t)
i (t)
2
1
b)
i (t)
3
c)
E
E=0
3
1
i (t)
H×nh 3.52.
R
1
2
R
i (t)
K
i (t)
K
LE
L
K
E
R
R
2
R
1
i
i
1
i
2
H×nh 3.51
5
t
1
i
1
(t)
i
2
(t)
[s]
10
i
1
(t)=i
2
(t)
i
K
(t)
H×nh 3.53
[V]
1
i (t)
R
1
2
2
R
i (t)
K
i (t)
K
L
E
a) b)
98
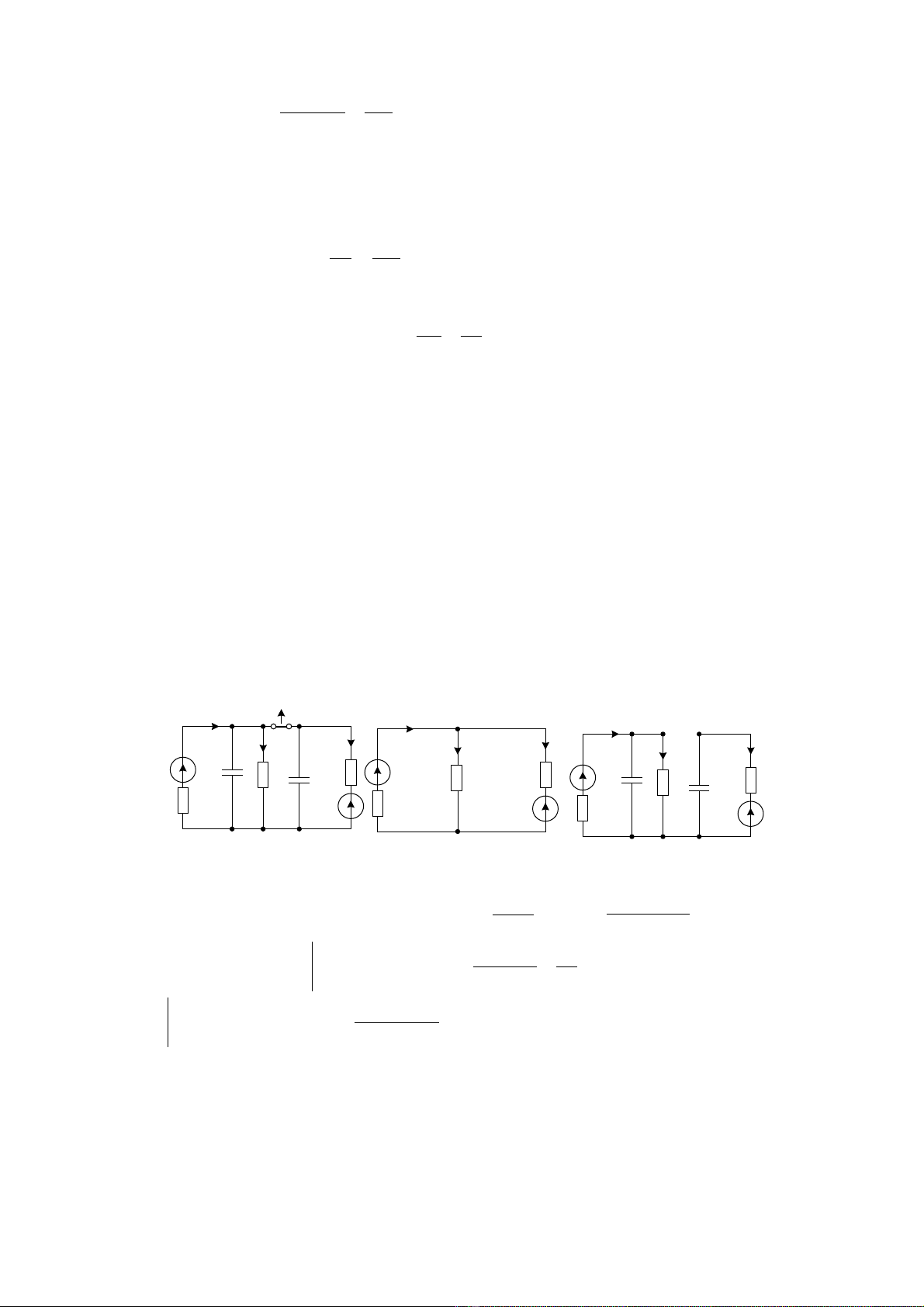
A
RR
E
)(i)(iI 5
20
100
00
21
210 ==
+
===
; iK=0. Đây là tr ng thai kh i đi m c aạ ở ể ủ
m chạ
Khi đóng K: M ch g m 2 ph n đ c l p nhau, nh ng t o thành 2 dòng dùng điạ ồ ầ ộ ậ ư ạ
qua khoá K. Hình 3.53a)
M ch bên trái g m Rạ ồ 1 và E là m ch thu n tr nên: ạ ầ ở
;A
R
E
i
R10
10
100
1
1===
M ch bên ph i là s phóng đi n t do c a L qua Rạ ả ự ệ ự ủ 2:
( ) ( )
;Aeti;
,L
R
;Ae)t(iti t
R
t
LR
100
2
2
22 100
10
10 −α− ====α==
Vì i2(0)=5 nên A=5 → i2(t) =5e-100t. Khi t=1s thì i2(1)≈0;
iK(t)=i1(t)-i2(t)=10-5e-100t
Khi h K ởm ch l i có iạ ạ 1(t)=iL(t)=iR2(t) bi n thiên theo quy lu t hàm mũ nênế ậ
i1(t)=iL(t)=i2(t)=Be-α1(t-1)+C=
;
)( CBe 1t2000 +
−−
);e()t(inªnB)s(i)s(i;AIC )t(
LXL
12000
1550115 −−
−=−=⇒====
Đ th hình 3.53b)ồ ị
3.8.M ch đã cho trên hình 3.54a): ạ
Tìm đi u ki n ban đ u, t c tìm ề ệ ầ ứ UC1(0) và UC2(0): Tr c khi h khoá Kướ ở
m ch ch đ m t chi u xác l p, không có dòng qua Cạ ở ế ộ ộ ề ậ 1 và C2 nên s đ t ngơ ồ ươ
đ ng có d ng hình 3.54.b). ươ ạ
Gi i m ch m t chi u tìm đ c iả ạ ộ ề ượ 1(0)=1,44A; i3(0)=0,4A, i2(0)=1,44-0,4=1,04A
UC1(0)=UC2(0)=UR2(0)=1,05.15 =15,6V.
Sau khi h khoá K:ở M ch tách là hai ph n đ c l p nhau (hình 3.54.c):ạ ầ ộ ậ
Ph n m ch bên trái:ầ ạ
121 6
25
1510 α=== ;
.
R//RR td
=
333
105006
1
6≈
−
..
[1/s]
i1(t)=A1e-333t+B1;
21
25
30
21
1
111 ,
RR
E
B)(i
t
)t(i ==
+
==∞=
∞⇒
21240240441
0
0
0
333
11
1
1
1111 ,e,)t(i;,A;,
R
)(UE
BA)(i
t
)t(i t
C+===
−
=+==
=
−
[A]
R
R
1
2
1
3
K
R
C
C
E
E
1
2
2
1
i (t)
3
i (t) i (t)
2
R
R
1
2
1
3
R
E
E
2
H×nh 3.54
R
R
1
2
1
3
R
C
C
E
E
1
2
2
1
i (t)
3
i (t) i (t)
2
a) b) c)
i (0)
1
i (0)
3
i (0)
2
99
uR1(t)=R1i1(t)=2,4e-333t+12[V]; uR2(t)=uC1(t)=E1-uR1(t)=18-2,4e-333t[V]
[ ]
Ae,)t(i)t(i)t(i;]A[e,,
R
)t(u
)t(i t
C
t
R333
211
333
2
2
24016021 −− =−=−==
Ph n m ch bên ph i:ầ ạ ả
5555
1
9
23
23 ,
CR
;RR td ==α==
; i3(t)=A2e-555t+B2.
0
233 ==∞=
∞⇒ B)(i
t
)t(i
vì dòng 1 chi u không qua đ c Cề ươ 2.
t
Ce,)t(i;,
R
E)(U
A)(i
t
)t(i 555
3
3
22
233 4040
0
0
0
−
==
−
===
=
[A]
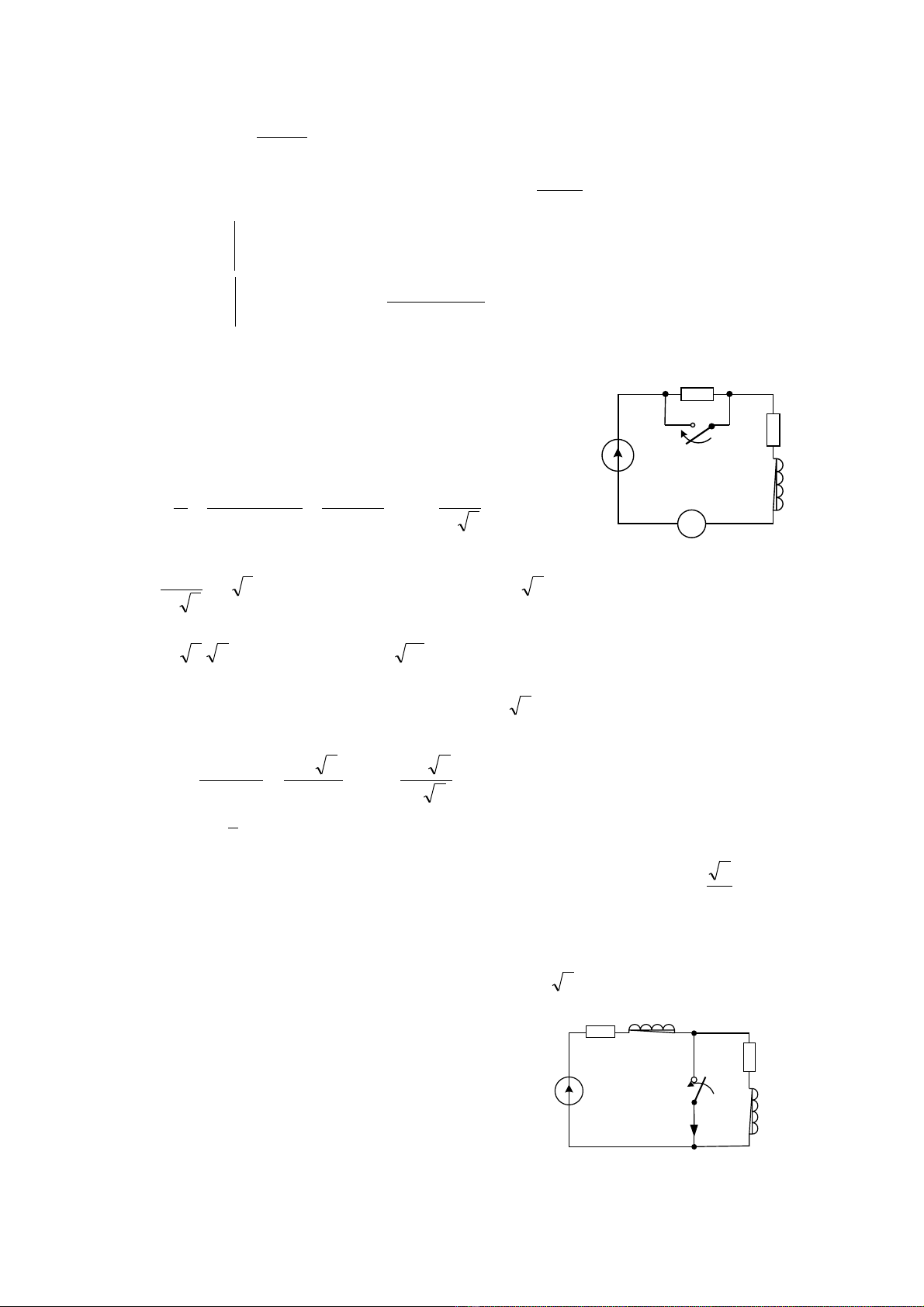
3.9. Hình 3.55.
Vì ngu n chuy n qua giá tr max d ng t iồ ể ị ươ ạ
t=0 nên αe=900, t c e(t)=Eứmsin(100t+900)[V]
Xác đ nh đi u ki n ban đ u:ị ề ệ ầ t c iứL(0)=?
Dòng xác l p hình sin khi ch a đóng khoá K:ậ ư
;e
E
e
j
E
,.j
eE
Z
E
I,j
m
j
m
j
m
.
.
m
00
0
436390
90
510
10201010020 =
+
=
+
==
Lúc này Ampe k ch gía tr hi u d ng nên:ế ỉ ị ệ ụ
]V[E;]V[E;]A[
E
Im210010052
510 ====
Tr c khi đóngướ
khoá K dòng đi n có bi u th c:ệ ể ứ
i(t)=
),tsin(),tsin(. 00 43631001024363100252 +=+
→đi u ki n ban đ u làề ệ ầ
IL0=5,66A
Bi u th c c a ngu n: e(t)=100ể ứ ủ ồ
2
sin(100t+900)[V]
+Sau khi đóng khoá K: i=it doự+ic ng b cưỡ ứ =itd+iCb
]A[)tsin(e,)t(i
,,m;sinm,)(i;)tsin(m e)t(i
Aem ei
)tsin(i;eee
jjXR
E
I
t
t
t
t
L
R
td
C b
j)(jj
L
.
m
m C b
.
0100
00100
100
045459090
451001041
41
2
2
10665451066504510010
451001010
210
2100
1010
2100 0000
++−=
−=−=+==++=
==
+===
+
=
+
=
−
−
−
−
−
3.10.
)tsin(e)t(i t0314 903141212 −+= −
;
;]V)[et(sin)t(u t
L
314
314120 −
−=
]V[)]tsin()t(e];V[)tcos(e)t(u t
R
0314 453142120314120120 −=−= −
3.11. Hình 3.56.
t,
Le)t(i 7125
26−
=
H×nh 3.55
K
e(t)
R
0
R
L
A
1
i (t)
H×nh 3.56.
R
1
22
R
i (t)
K
i (t)
KLE
100
)tcos(ee
)t(i)t(i)t(i
)tcos(e)t(i
t,t
K
t
07125418
21
0418
1
3731420610
373142010
−+−−
=−=
−+−=
−−
−
3.12. a)uC(t)=200(1-e-4t)
b)R=5 KΩ ;C=50 µF.
3.13. Hình 3.13.
a) uC(t)=uR(t)=100e-20t; i(t)=2e-20t;
b) WR(t)=5(1-e-40t) ;t1≈17,33 mS.
3.14.
Jun,
e
dteW;e
e
)t(p;eu)b
;Jun,.W;V)(uU);e(u)a
t
t
R
t
t
R
t
R
ECp¹nC
t
C
10
0
80
888
5000
200
200
10
2
200
1052001200
80
0
8080
2
402
40
2
640
=
∞
−
=====
===∞=−=
−
∞−−
−
−
−−
∫
3.15. a)Ngu n đi n áp:ồ ệ
s,;,R td 5151 =τΩ=
b) Ngu n dòng:ồ
s;R td 22 =τΩ=
3.16. M ch đi n hình 3.57. ạ ệ
Sau khi đóng khoá K, vì ngu n là lý t ng nên:ồ ưở
-Có dòng đ c l p qua Rộ ậ 1 là i1(t)=E/R1=2[A]
-C đ c n p qua Rượ ạ 2 theo quy lu t hàm mũậ
)e()e(Eu
t
t
CR
C
500
1
11501
2
−
−
−=−=
[V]
t
C
Ce
dt
du
C)t(i)t(i 500
26−
===
[A]
T i th i đi m t=1 s thì uạ ờ ể C(1s)=150(1-e-500)≈150V (đây là đi u ki n ban đ uề ệ ầ
khi h K).ở
Sau khi h khoá K:ởlúc đó C phóng đi n qua Rệ1 và R2 t giá tr uừ ị C(1s)=150V theo
quy lu t hàm mũ:ậ
uC(t)=150e
)t(
t
)RR(C e1125
21
1
150 −−
+
−=
[V] ;
]A[e,
RR
)t(u
)t(i )t(
C1125
21
151 −−
=
+
=
;
]A[e,
dt
du
Chaye,)t(i)t(i)t(i )t(
C
)t(
C
11251125
12 5151 −−−− −==−=−==
3.17. M ch đi n hình 3.58 ạ ệ
a) Đi n áp n p cho t : uệ ạ ụ C(t)=E(1-e-αt) v i ớ
R C
11 =
τ
=α
=1000
H×nh 3.57
C
ERR
21
K
i
i
2
1
H×nh 3.58
E
R
C
K
101