y
z
x
M N
QP
α
β
dy
y
v
v
∂
∂
+
y
x
M1
P(x,y+dy)
M(x,y) N(x+dx,y)
U
V
dx
dy
N2
N1
P1
O
dx
x
v
v
∂
∂
+
dy
y
u
u
∂
∂
+
dx
x
u
u
∂
∂
+
CH NG 3ƯƠ
LÝ THUY T TR NG THÁI CHUY N V VÀ BI N D NGẾ Ạ Ể Ị Ế Ạ
§3.1. PH NG TRÌNH QUAN H GI A CHUY N V VÀ BI N D NGƯƠ Ệ Ữ Ể Ị Ế Ạ
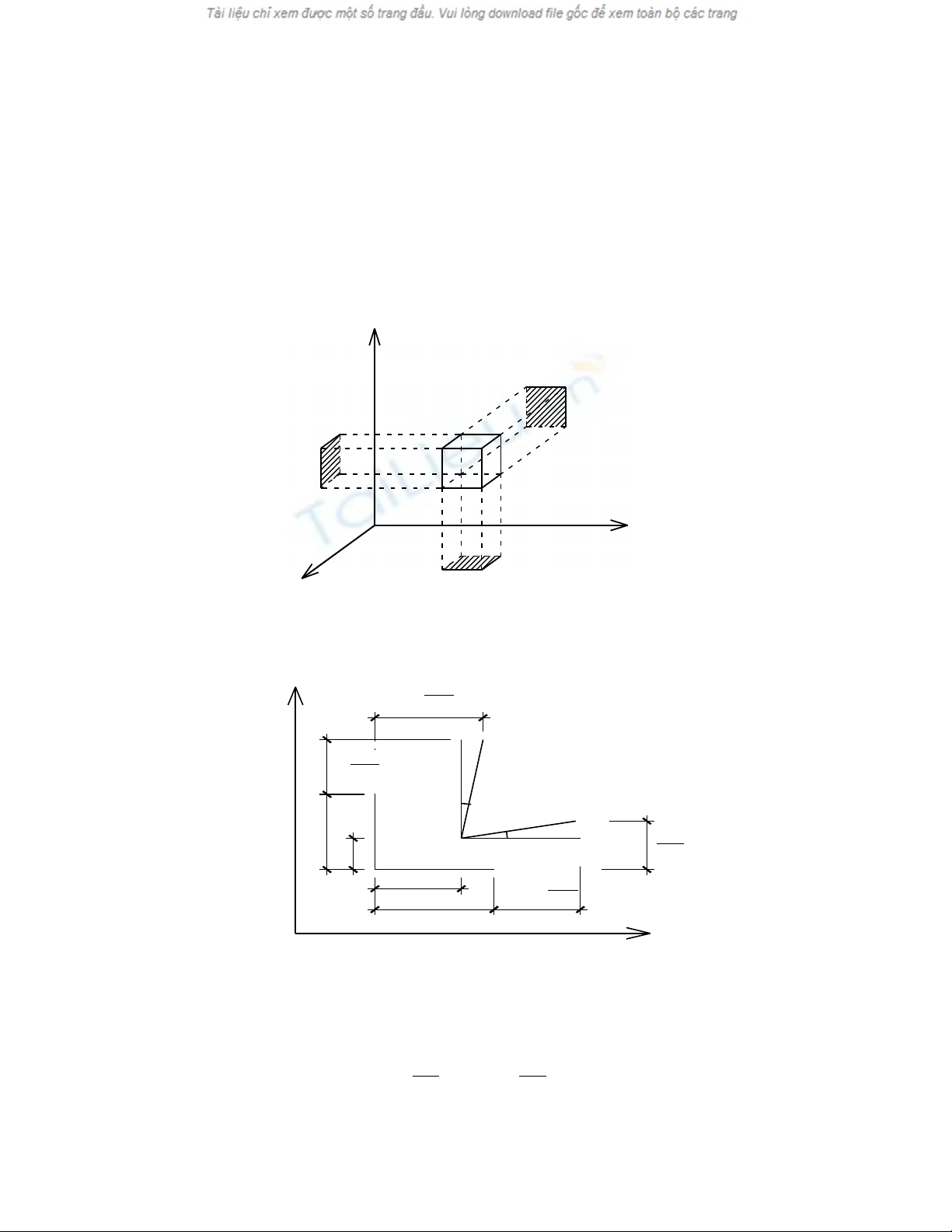
Xét bi n d ng c a ph n t v t ch t l y t i đi m M(x,y,z). V i cácế ạ ủ ầ ử ậ ấ ấ ạ ể ớ
bi n d ng là bé, ta có th quan sát bi n d ng c a ph n t qua bi n d ng cácế ạ ể ế ạ ủ ầ ử ế ạ
hình chi u c a nó trên các m t ph ng t a đ .ế ủ ặ ẳ ọ ộ
(Hình 3.1)
+ Xét bi n d ng trong m t ph ng xoy (H.3.2). Phân t ch nh t MNQP v iế ạ ặ ẳ ố ữ ậ ớ
các c nh ban đ u dx, dy sau bi n d ng tr thành phân t Mạ ầ ế ạ ở ố 1N1Q1P1.
(Hình 3.2)
- Đi m M(x,y) có chuy n v theo ph ng x,y là : u; v.ể ể ị ươ
- Đi m N(x+dx,y) có các chuy n v theo ph ng x,y, khai tri n Taylor b quaể ể ị ươ ể ỏ
các vô cùng bé b c cao là : u + ậ
dx.
x
u
∂
∂
; v+
dx.
x
v
∂
∂
15

- Đi m P(x,y+dy) có các chuy n v theo ph ng x,y là : u + ể ể ị ươ
dy.
y
u
∂
∂
; v+
dy.
y
v
∂
∂
- Bi n d ng dài t ng đ i c a các c nh theo ph ng x,y là ế ạ ươ ố ủ ạ ươ εx , εy.
- Bi n d ng góc trong m t ph ng đang xét xoy là ế ạ ặ ẳ γxy = α+β.
Theo gi thi t bi n d ng bé, ta có : ả ế ế ạ /εx /<< 1; /εy /<< 1; /α/ << 1; /β/ << 1
S d ng các công th c g n đúng : ử ụ ứ ầ
1cos;1cos
tgsin;sintg
≈β≈α
β≈β≈βα≈α≈α
3.1.1.Tính bi n d ng dài t ng đ i :ế ạ ươ ố
Ta có :
MN
MNNM 11
x
−
=ε
(a)
Trong đó : MN = dx
M1N1 =
21
21
11 NM
cos
NM
NM ≈
α
=
T hình v ta có : ừ ẽ
dx)
x
u
1(udx.
x
u
udxNM 21 ∂
∂
+=−
∂
∂
++=
x
u
dx
dxdxdx)
x
u
1(
MN
MNNM
)a( 11
x∂
∂
=
−+
∂
∂
+
=
−
=ε⇔
T ng t ta có : ươ ự
y
v
y∂
∂
=ε
(b)
3.1.2.Tính bi n d ng góc: ế ạ γxy = α+β
Góc quay c a c nh MN s là : ủ ạ ẽ
α ≈ tgα =
21
21
NM
NN
=
x)
x
u
1(
v)dx
x
u
v(
∂
∂
∂
+
−
∂
∂
+
=
x
u
1
x
v
∂
∂
+
∂
∂
=
x
1
x
v
ε+
∂
∂
Theo gi thi t bi n d ng bé ta có ả ế ế ạ εx << 1 có th b qua ể ỏ εx so v i 1 ớ
16
z
y
n
K
x
dy
dx
dz
M
y
z
x
M1
K1
α =
x
v
∂
∂
T ng t ươ ự β =
y
u
∂
∂
=> γxy = α+β=
x
v
∂
∂
+
y
u
∂
∂
(c)
Các k t qu (b) và (c) cho trong m t ph ng xoy đ c s d ng cho hai m tế ả ặ ẳ ượ ử ụ ặ
ph ng còn l i yoz và zox. B ng cách hoá v vòng các ch s theo th t c aẳ ạ ằ ị ỏ ố ứ ự ủ
tam di n thu n x,y,z ta nh n đ c quan h chuy n v và các bi n d ng nhệ ậ ậ ượ ệ ể ị ế ạ ư
sau :
x(u)
y(v) z(w)
∂
∂
+
∂
∂
=γ
∂
∂
=ε
∂
∂
+
∂
∂
=γ
∂
∂
=ε
∂
∂
+
∂
∂
=γ
∂
∂
=ε
x
w
z
u
;
z
w
)1.3(
z
v
y
w
;
y
v
y
u
x
v
;
x
u
zxz
yzy
xyx
Công th c (3.1) thi t l p m i quan h tuy n tính gi a các thành ph nứ ế ậ ố ệ ế ữ ầ
bi n d ng và các chuy n v xét th i đi m t, đế ạ ể ị ở ờ ể ư c g i là ph ng trình quanợ ọ ươ
h hình h c CAUCHY ệ ọ
T (3.1) có th k t lu n các bi n d ng là bé khi đ o hàm b c nh t cácừ ể ế ậ ế ạ ạ ậ ấ
chuy n v theo ph ng to đ là bé.ể ị ươ ạ ộ
§3.2 TR NG THÁI BI N D NG - TENXẠ Ế Ạ Ơ BI N D NGẾ Ạ
3.2.1.Bi n d ng dài t ng đ i theo ph ng b t kỳ :ế ạ ươ ố ươ ấ
H (3.1) cho phép ta tính bi n d ng dài tệ ế ạ ương đ i theo các ph ngố ươ
x,y,z. Đ t v n đ làm sao tính bi n d ng dài tặ ấ ề ế ạ ương đ i theo ph ng b t kỳ ?ố ươ ấ
17

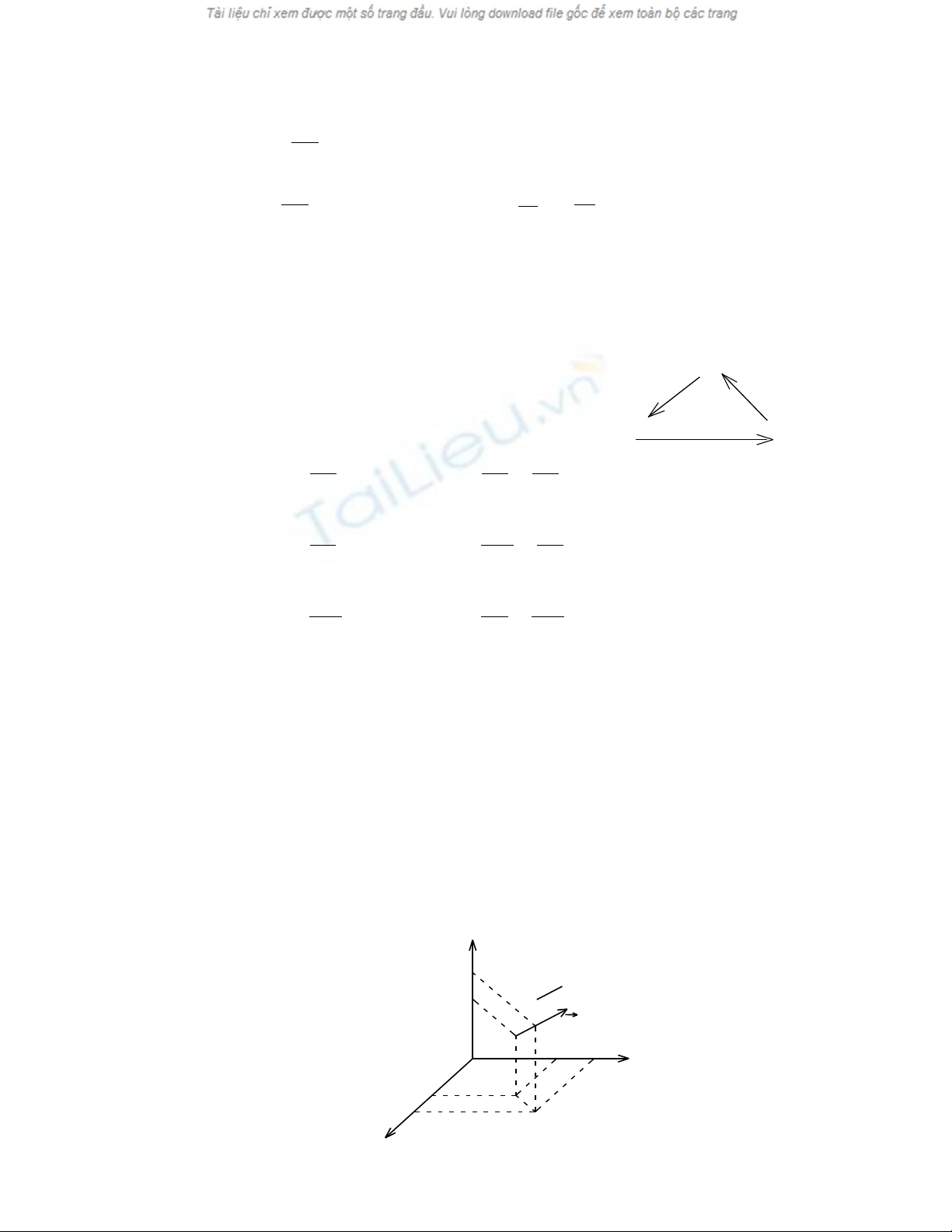
(Hình 3.3)
Trong h tr c to đ Descartes.Xét vi phân chi u dài MK= ds theoệ ụ ạ ộ ề
ph ng n v i các cosin ch ph ng là l,m,n.ươ ớ ỉ ươ
Hình chi u c a ds lên các tr c x,y,z là dx, dy, dz.ế ủ ụ
l = cos (
x,n
) =
ds
dx
cóntoVéc
m = cos (
y,n
) =
ds
dy
(a)
n = cos (
z,n
) =
ds
dz
+ tr ng thái ban đ u, to đ đi m đ u và đi m cu i c a vi phân MKỞ ạ ầ ạ ộ ể ầ ể ố ủ
là M(x,y,z) và K(x+dx, y+dy, z+dz)
+Đi m M(x,y,z) chuy n v theo ba ph ng x,y,z là u,v, w. ể ể ị ươ
+Đi m K(x+dx, y+dy, z+dz) chuy n v theo ba ph ng là : u+du; v+dv;ể ể ị ươ
w+dw.
V i du, dv, dw là các vi phân toàn ph n c a thành ph n chuy n v u,v,w.ớ ầ ủ ầ ể ị
du =
x
u
∂
∂
.dx +
y
u
∂
∂
.dy +
z
u
∂
∂
.dz
dv =
x
v
∂
∂
.dx +
y
v
∂
∂
.dy +
z
v
∂
∂
.dz
dw =
x
w
∂
∂
.dx +
y
w
∂
∂
.dy +
z
w
∂
∂
.dz
+ Sau bi n d ng MK ế ạ tr thànhở M1K1 = ds1 trong đó :
M(x,y,z) tr thành Mở1( x+u, y+v, z+w).
K(x+dx, y+dy, z+dz) tr thành Kở1(x+dx+u+du, y+dy+v+dv,
z+dz+w+dw).
+ Chi u dài vi phân tr c bi n d ng: dsề ướ ế ạ 2 = dx2 + dy2 + dz2 (b)
+ Chi u dài vi phân dsề1 sau bi n d ng: ế ạ
ds12 = (dx+du)2 + (dy+dv)2 + (dz+dw)2 (c)
Bi n d ng dài t ng đ i theo ph ng n c a ds. Ký hi u ế ạ ươ ố ươ ủ ệ εn là :
εn =
ds
dsds1−
=
ds
ds
1
- 1
(εn + 1)2 =
2
2
1
ds
ds
1+2εn + εn2 =
2
2
1
ds
ds
εn =
2
2
2
1
ds2
dsds −
(d)
(V i gi thi t bi n d ng bé có th b qua ớ ả ế ế ạ ể ỏ εn2 so v i ớεn)
18

Tính ds12 = [dx + (
x
u
∂
∂
.dx +
y
u
∂
∂
.dy +
z
u
∂
∂
.dz)]2 +
+ [dy + (
x
v
∂
∂
.dx +
y
v
∂
∂
.dy +
z
v
∂
∂
.dz)]2 +
+ [dz + (
x
w
∂
∂
.dx +
y
w
∂
∂
.dy +
z
w
∂
∂
.dz)]2. (e)
Khai tri n (e) và b qua các thành ph n vô cùng bé b c cao ể ỏ ầ ậ
(
x
u
∂
∂
.dx+
y
u
∂
∂
.dy+
z
u
∂
∂
.dz)2;(
x
v
∂
∂
.dx+
y
v
∂
∂
.dy+
z
v
∂
∂
.dz)2;(
x
w
∂
∂
.dx+
y
w
∂
∂
.dy+
z
w
∂
∂
.dz)2 so v iớ
x
u
∂
∂
;
y
v
∂
∂
;
z
w
∂
∂
...(vì theo gi thi t bi n d ng bé ả ế ế ạ
x
u
∂
∂
;
y
v
∂
∂
;
z
w
∂
∂
... << 1) và rút g n :ọ
(e) ds12 = (dx2 + dy2 + dz2) + 2 [(
x
u
∂
∂
.dx2 +
y
u
∂
∂
.dxdy +
z
u
∂
∂
.dxdz) +
+ (
x
v
∂
∂
.dxdy +
y
v
∂
∂
.dy2 +
z
v
∂
∂
.dydz) +
+ (
x
w
∂
∂
.dxdz +
y
w
∂
∂
.dydz +
z
w
∂
∂
.dz2)].
ds12 - ds2 = 2 [(
x
u
∂
∂
.dx2 +
y
u
∂
∂
.dxdy +
z
u
∂
∂
.dxdz) +
+(
x
v
∂
∂
.dxdy +
y
v
∂
∂
.dy2 +
z
v
∂
∂
.dydz) +
+ (
x
w
∂
∂
.dxdz +
y
w
∂
∂
.dydz +
z
w
∂
∂
.dz2)].
Theo (d)
2
2
2
1
n
ds2
dsds −
=ε
=>
.
ds
dz
.
z
w
ds
dydz
.
y
w
ds
dxdz
.
x
w
ds
dydz
.
z
v
ds
dy
.
y
v
ds
dxdy
.
x
v
ds
dxdz
.
z
u
ds
dxdy
.
y
u
ds
dx
.
x
u
2
2
22
22
2
2
222
2
n
∂
∂
+
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
+
∂
∂
=ε⇔
Thay
ds
dz
n;
ds
dy
m;
ds
dx
l===
và bi u th c (3.1) vào ể ứ εn :
⇒ εn = εx.l2 + εy.m2 + εz.n2 + γxy.lm + γyz.mn + γzx.nl (3.4).
19




![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










