Lý thuyết tín hiệu
Lecturer: M.Eng. P.T.A.Quang
Chương 4: Biến đổi Fourier cho th liên tục
Biến đổi Fourier cho th liên tục
Những tính chất biến đổi Fourier cho tín hiệu liên tục
Hệ thống đặc trưng bởi ptvp hệ số hằng
Biến đổi Fourier cho th liên tục
Biến đổi Fourier

dejXtx tj
)(
2
1
)(

dtetxjX tj
)()(
Phổ biên độ
Phổ pha
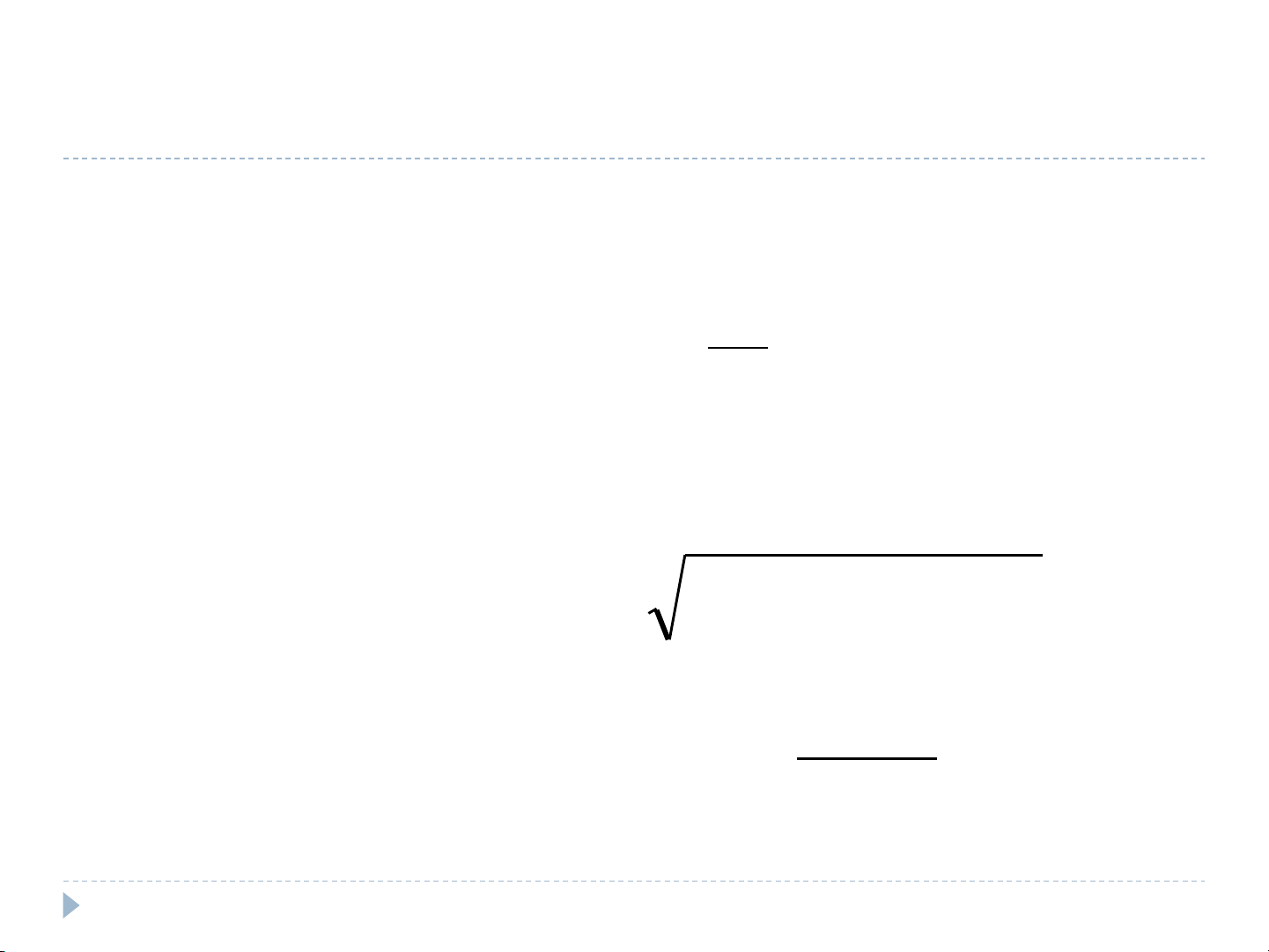
)()(|)(| 22
bajX
)(
)(
tan)( 1
a
b
jX
)()()(
jbajX
Nếu
Biến đổi Fourier cho th liên tục
Ví dụ: tìm phổ biên độ và phổ pha của tín hiệu
0),()(
tuetx t
Biến đổi Fourier cho th liên tục
Ví dụ: tìm phổ của tín hiệu
)()( ttx