1
Chương 4
BIẾN ĐỔI Z
Chương này giới thiệu biến đổi z mà rất hữu ích trong phân tích và thiết kế hệ thống DSP (hoặc
DTSP), giống như biến đổi Laplace cho hệ thống tương tự (hoặc liên tục thời gian). Phân tích Fourier
được phát triển cho miền liên tục thời gian nhưng cũng hữu ích cho tín hiệu và hệ thống rời rạc thời
gian. Ta sẽ thấy biến đổi z và biến đổi Fourier liên hệ với nhau. Ta chọn để trình bày biến đổi z sau
phân tích Fourieer như nhiều tác giả khác đã làm, nhưng theo trật tự ngược lại cũng thường thấy.
Chủ đề chính là: định nghĩa biến đổi z, hữu ích đôi biến đổi, thuộc tính biến đổi, vẽ cực và
không, vùng hội tụ, sự ổn định của hệ thống, biến đổi ngược, biến đổi z một bên, lọc bậc hai, đáp ứng
chuyển tiếp và hệ thống với điều kiện đầu
4.1 BIẾN ĐỔI Z
Phần mở đầu bao gồm nhiều khía cạnh khác nhau của biến đổi z. Giống như những biến đổi khác,
biến đổi z áp dụng cho cả tín hiệu và hệ thống rời rạc. Ta biết rằng một hệ thống được đặc trưng bởi
phương trình tín hiệu vào ra, hoặc đáp ứng xung của nó, hoặc đáp ứng tần số. Tóm lại ta sẽ thấy đặc
tính thứ tư của hệ thống.
4.1.1 Định nghĩa: Biến đổi z X(z) của một tín hiệu rời rạc thời gian x(n) được định nghĩa như
X(z) =
()
∞
-n
n = 0
x n z
(4.1)
z là một biến phức của miền biến đổi và có thể xem như tần số phức (xem hình 4.5). Nhớ rằng chỉ số
n có thể là thời gian, không gian hoặc một số thứ khác, nhưng thường là thời gian. Như định nghĩa
trên, X(z) là chuỗi mũ nguyên của
1
z
tương ứng với những hệ số x(n). Khai triển X(z) để thấy điều
này:
X(z) =
0
() n
n
x n z
= x(0) + x(1)z-1 + x(2)z-2 + . . . (4.2)
Trong công thức (4.1) tổng được lấy từ n = 0 đến
, X(z) không liên hệ với thời gian quá khứ
x(n). Đây là biến đổi z một bên. Biến đổi z một bên có thể có thể với điều kiện đầu của x(n) (phần
4.7). Nhìn chung, tín hiệu tồn tại tại mọi thời gian, và biến đổi z hai bên được định nghĩa như:
X(z) =
∞
-n
n= -∞
z
xn
= …x(-2)z
2
+ x(-1)z + x(0) + x(1)z
1
+ x(2)z
2
+ … (4.3)
Vì X(z) là một chuỗi mũ vô hạn của
1
z
, biến đổi chỉ tồn tại những giá trị nơi chuỗi hội tụ (tiến tới
không khi n
hoặc -
). Vì vậy biến đổi z liên hệ mật thiết với vùng hội tụ (ROC) nơi nó là hữu
hạn (phần 4.4). Để phân biệt, ta chú thích
)(zX
cho biến đổi z một bên.
Ví dụ 4.1.1
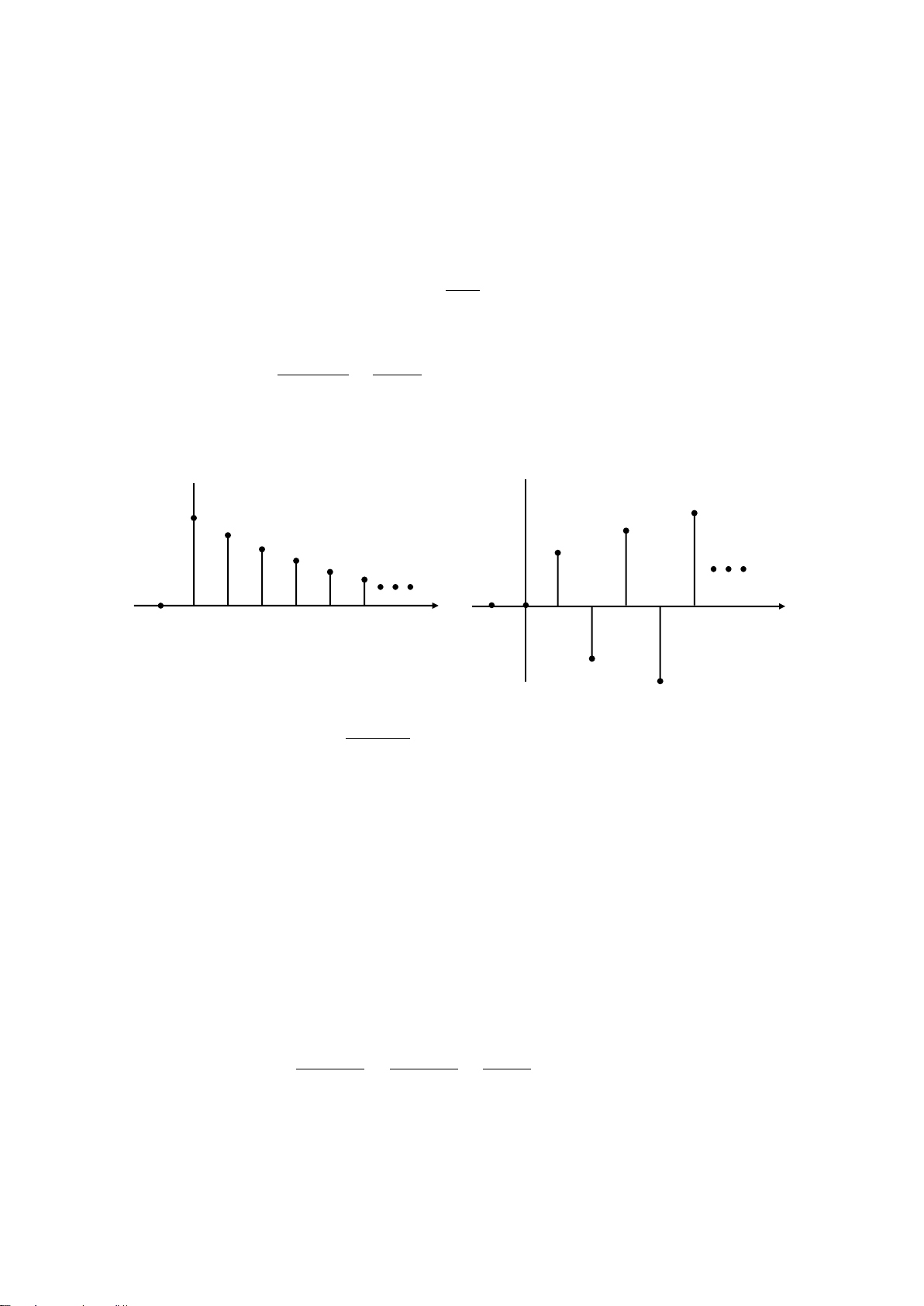
Tìm biểu diễn toán học của tín hiệu trong hình 4.1, sau đó tìm biến đổi z.
Giải
(a) Chú ý tín hiệu là nhân quả và giảm đều , nó có giá trị
với n
0. Vì vậy ta viết
x(n) = 0.8n u(n)
và sử dụng biến đổi (4.1)
2
X(z) =
0n
n
znx )(
= 1 + 0.8z–1 + 0.64z–2 + 0.512z–3 +…
= 1 + (0.8z–1) + (0.8z–1)2 + (0.8z–1)3 + …
Ap dụng công thức chuỗi hình học vô hạn (2.8)
1 + x + x2 + x3 + … =
0
n
n
x
=
1
1x
, x< 1 (4.4)
Với
1
0.8xz
ta có
X(z) =
1
0.81
1
z
=
80.z
z
Kết quả có hình thức của cả hai bên. Điều kiện
1
| 0.8 | 1z
nghĩa
| | 0.8z
.
(b) Tín hiệu thây đổi dương âm với giá trị tăng. Tín hiệu phân kỳ. Sau một vài lần thử, ta cso
thể quyết định biểu diễn toán học của nó như:
x(n) = (-1.2)n–1 u(n-1) (4.5)
Với
n
).( 21
u(n) trễ một đơn vị. Sử dụng công thức (4.1) ta có
X(z) =
0n
n
z)nx(
= 0 + 1.0(z–1) – 1.2(z–1)2 + 1.44(z–1)3 – 1.718(z–1)4 + …
= z–1 [1 + (-1.2z–1) + (-1.2z–1)2 + (-1.2z–1)3 + …]
= z–1
1
z.
211
1
=
1
1
211
z.
z
=
21
1
.z
4.1.2 Biến đổi z đảo
Tín hiệu x(n) và biến đổi của nó X(z) là một đôi biến đổi
X(z)x(n) z
(4.6)
n
x(n)
1
0.8
0.64
0.512
1
-1
0
2
3
4
5
(a)
0
n
x(n)
-1
1
2
3
4
5
1
-1.2
1.44
-1.728
Hình. 4.1:Ví dụ 4.1
(a)
(b)
3
Một cách để tìm biến đổi ngược, bất kỳ khi nào có thể, là sử dụng định nghĩa biến đổi z. Phương pháp
tổng quát của biến đổi z ngược sẽ được thảo luận trong phần 4.5 và 4.6
Ví dụ 4.1.2
Tìm biến đổi z ngược của những biểu thức sau
(a) X(z) =
80.z
z
(b) X(z) =
21
1
.z
Giải
(a) Lấy khai triển X(z) sử dụng chuỗi hình hoc vô hạn:
X(z) =
80.-z
z
=
1
801
1
-
z.-
= 1 + (0.8z–1) + (0.8z–1)2 + (0.8z–1)3 + …
= 1 + 0.8z–1 + 0.64z–2 + 0.512z–3 + …
Bằng cách so sánh từ thành phần với từng thành phần trong công thức (4.2) ta có
x(n) = [1 , 0.8 , 0.64 , 0.512 ; …]
Hoặc
x(n) =
)u(8.0 n
n
(b) Biểu diễn được cho không giống như được biến đổi, vì vậy ta viết.
X(z) =
1
1.2z
=
1
1
1 1.2
z
z
=
1
1
1
1 1.2
zz
Kế đến, lấy khai triển X(z) :
X(z) = z–1 [1 + (-1.2z–1) + (-1.2z–1)2 + (-1.2z–1)3 + …]
= 0 + 1.0z–1 – 1.2z–2 + 1.44z–3 – 1.728z–4 + …
Vì vậy
x(n) = [0 ,1.0 , -1.2 , 1.44 , -1.728 , …]
Mà có thể diễn tả trong hình thức đóng như sau
x(n) = (–1.2)
1n
u(n-1)
4.1.3 Đôi biến đổi z
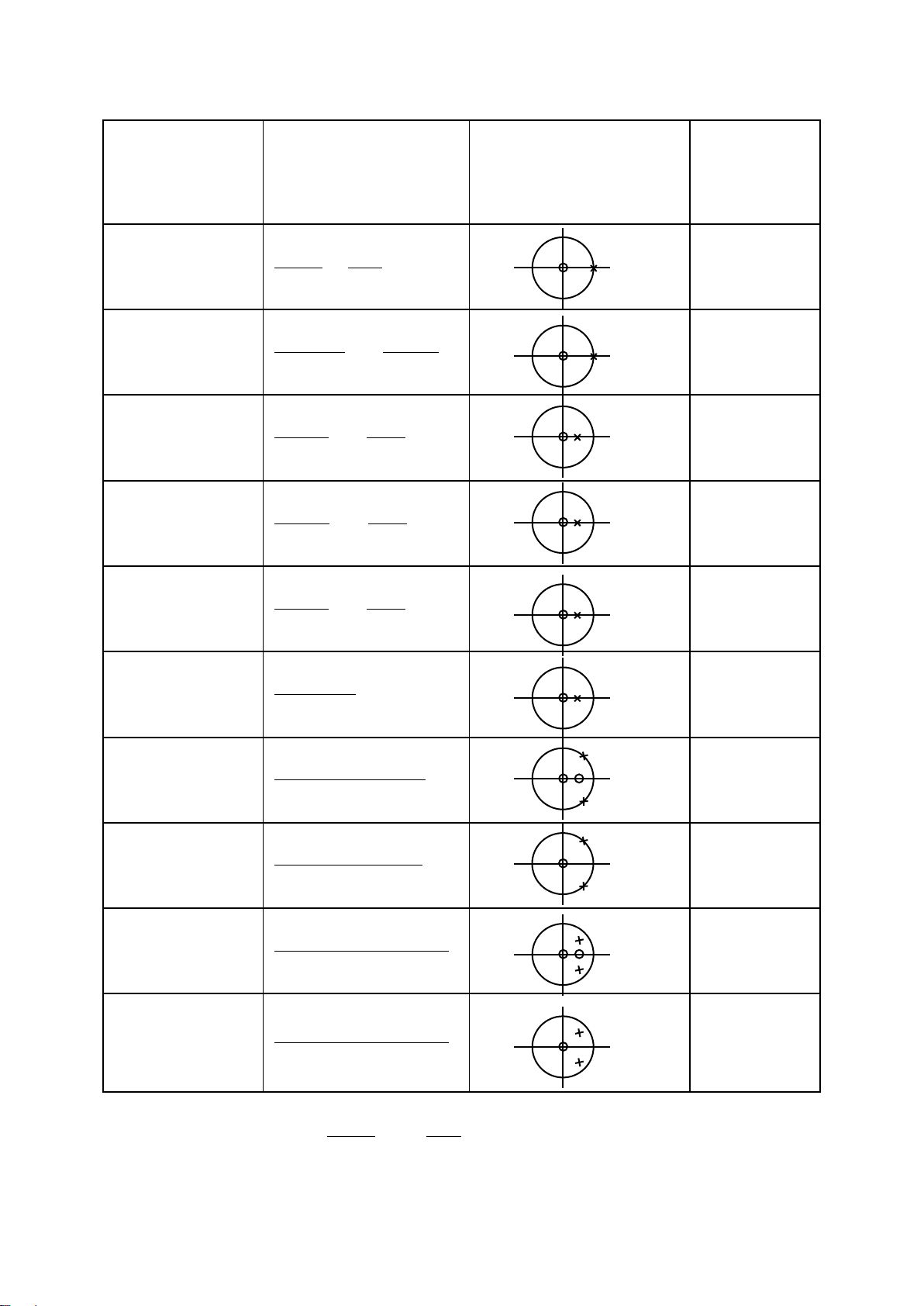
Bảng 4.1 đưa ra nhiều đôi biến đổi z hữu ích, nơi vòng tròng đơn vị là vòng tròn có bán kính 1tâm tại
gốc. Tất cả tín hiệu là nhân quả (bên phải), ngoại trừ hai tín hiệu phi nhân quả (bên trái). Chú ý rằng
một biến đổi có thể diễn tả tương đương như một hàm
1
z
hoặc z , ví dụ
Bảng 4.1 : Đôi biến đổi z thông thường
Tín hiệu x(n)
Biến đổi X(z)
Giảng đồ cực -không
ROC
-j
j
-1
1
Unit circle
0
4
Mẫu đơn vị
(n)
1
Tất cả z
Bậc đơn vị
u(n)
)
1
(
1
1
1
z
z
z
z> 1
Dốc đơn vị
r(n) = nu(n)
221
1
11 )(z
z
)z(
z
-
-
z> 1
Mũ thực
an u(n)
0 < a < 1
az
z
az-1
1
1
z > a
Mũ thực
(-a)n u(n)
0 < a < 1
az
z
az-1
1
1
z > a
-an u(-n-1)
(phi nhân quả)
0 < a < 1
az
z
az-1
1
1
z < a
-nan u(-n-1)
(phi nhân quả)
0 < a < 1
21
1
1)az(
az
z < a
Cosine
(cosn
0) u(n)
2
0
1
0
1
cos21
ωcos1
zωz
z
z> 1
Sine
(sinn
0) u(n)
2
0
1
0
1
ωcos21
ωsin
zz
z
z> 1
Cosine tắt dần
(ancosn
0) u(n)
22
0
1
0
1
ωcos21
ωcos1
zaaz
az
z > a
Sine tắt dần
(ansinn
0) u(n)
22
0
1
0
1
ωcos21
ωsin
zaaz
az
z > a
u(n) X(z) =
1
1
1
z
or
1z
z
(4.7a)
double
double
5
anu(n) X(z) =
1
1
1
az
or
az
z
(4.7b)
(cosn0)u(n) X(z) =
2
0
1
0
1
Ωcos21
Ωcos1
zz
z
or
1Ωcos2
Ωcos
0
2
0
zz
)z(z
(4.7c)
Hình thức có nhiều sự phụ thuộc vào cái ta muốn làm với biến đổi (xem phần 4.1.6 , 4.3 và 4.6).
4.1.4 Biến đổi z cho hệ thống
Biến đổi z áp dụng cho tín hiệu cũng như hệ thống vì hệ thống được trình bày bằng đáp ứng xung của
nó. Mà nó là hàm có chỉ số n giống như tín hiệu. Vì thuộc tính này mà biến đổi z hữu ích trong phân
tích và thiết kế hệ thống vì tín hiệu và hệ thống tương tác nhau.
Đặc biệt, biến đổi z của đáp ứng xung h(n) là
H(z) =
0n
n
znh )(
(Biến đổi 1 bên) (4.8)
Hoặc
H(z) =

n
n
zn)(h
(Biến đổi hai bên) (4.9)
Phụ thuộc hệ thống là nhân quả hoặc phi nhân quả. H(z) được gọi là hàm truyền hoặc hàm hệ thống
Ví dụ 4.1.3
Một hệ thống có đáp ứng xung
h(n) = [1 , 2 , 3 , 4 , 5 , 6]
Tìm hàm truyền.
Giải
Hệ thống là một FIR phi nhân quả. Hàm truyền của nó được cho bởi công thức (4.9):
H(z) =

n
n
zn)(h
=
3
2
)(h
n
n
zn
=
32112 65432 zzzzz
Ngược lại, nếu biết H(z) như trên ta có thể dễ dàng có h(n) .
4.1.5 Hàm riêng và trị riêng
Ta biết nếu đáp ứng tần số của một hệ thống là H(
) thì với ngõ vào x(n) =
jn
e
, ngõ ra là y(n) =
jn
e
H(
) như trong (3.69b). Vì điều này ,
jn
e
là hàm riêng, và H(
) là trị riêng của hệ thống.
Bây giờ, với đầu vào
x(n) = zn (4.10)
ngõ ra hệ thống là
y(n) = h(n) x(n) =
0k
kn
(k)zh
=
0k
kn (k)zhz
Trong ngoặc là H(z) , thì
y(n)
n
= z H(z)
(4.11)
Vì vậy trong miền biến đổi z,
n
z
là hàm riêng, và H(z) là trị riêng của hệ thống
4.1.6 Hàm truyền trong những thành phần của hệ số lọc
Đầu tiên, với phương trình lọc tổng quát (công thức (2.21))