Chương 4 PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

Chia sẻ: Phan Thiên Ân | Ngày: | Loại File: PDF | Số trang:5

Thêm vào BST

Báo xấu

363
lượt xem 25
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Đưa phương trình của (E) về dạng chính tắc: x y a b 2 2 2 2  1. Xác định a, b, c. Các yếu tố: – Độ dài trục lớn 2a, trục nhỏ 2b. – Tiêu cự 2c. – Toạ độ các tiêu điểm F1(c; 0), F2 (c;0) . – Toạ độ các đỉnh A1(a; 0), A2 (a;0), B1(0;b), B2 (0;b) . – Tâm sai e c a . 2. Trong trường hợp không có phương trình (E) khi đó ta đưa bài toán về xét các tam giác để xác định các yếu tố của (E)....

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Chương 4 PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

NHĐ PHƯƠNG PHÁP TỌA ĐỘ 4 TRONG MẶT PHẲNG Chương ĐƯỜNG ELIP VẤN ĐỀ 1: XÁC ĐỊNH CÁC YẾU TỐ CỦA ELIP x2 y2  1 . Xác định a, b, c. 1. Đưa phương trình của (E) về dạng chính tắc:  a2 b2 Các yếu tố: – Độ dài trục lớn 2a, trục nhỏ 2b. – Tiêu cự 2c. – Toạ độ các tiêu điểm F1(c; 0), F2 (c; 0) . – Toạ độ các đỉnh A1(a; 0), A2 (a; 0), B1 (0;  b), B2 (0; b ) . c Tâm sai e  – . a 2. Trong trường hợp không có phương trình (E) khi đó ta đưa bài toán về xét các tam giác để xác định các yếu tố của (E). Baøi 1. Cho elip (E). Xác định độ dài các trục, tiêu cự, toạ độ các tiêu điểm, toạ độ các đỉnh, tâm sai, phương trình các đường chuẩn của (E), với (E) có phương trình: x 2 y2 x 2 y2 x 2 y2 x 2 y2 1 1 1 1 a) b) c) d)     9 4 16 9 25 9 4 1 e) 16 x 2  25y 2  400 f) x 2  4 y 2  1 g) 4 x 2  9 y 2  5 h ) 9 x 2  25y 2  1 Baøi 2. Tìm tâm sai Elip biết : a) Mỗi tiêu điểm nhìn trục nhỏ dưới 1 góc 2 1 b) Khoảng cách giữa hai đỉnh trên 2 trục bằng k lần tiêu cự k  2 c) Đỉnh trên trục nhỏ nhìn hai tiêu điểm dưới 1 góc 2 HD: B1 a) Tìm tan  theo b và c, từ đó tính được e  cos b F2 O α c B2 2 b) Pitago trong tam giác vuông OA2B2, tìm b2 theo k, c. Kết quả : e  2 4k  1 c) Tương tự câu a). Kết quả e  sin  HTTH
NHĐ VẤN ĐỀ 2: LẬP PHƯƠNG TRÌNH CHÍNH TẮC CỦA ELIP Để lập phương trình chính tắc của (E) ta cần xác định độ dài các nửa trục a, b của (E). Chú ý: Công thức xác định các yếu tố của (E): c + b 2  a2  c 2 + e  a + Các tiêu điểm F1(c; 0), F2 (c; 0) + Các đỉnh: A1(a; 0), A2 (a; 0), B1 (0;  b), B2 (0; b ) Baøi 3. L ập phương trình chính tắc của (E), biết: a) Độ dài trục lớn bằng 6, trục nhỏ bằng 4. b) Độ dài trục lớn bằng 10, tiêu cự bằng 6. c) Độ dài trục lớn bằng 8, độ dài trục nhỏ bằng tiêu cự. d) Tiêu cự bằng 8 và đi qua điểm M  15; 1 . e) Độ dài trục nhỏ bằng 6 và đi qua điểm M  2 5; 2  . e) Một tiêu điểm là F1(2; 0) và độ dài trục lớn bằng 10.  3 f) Một tiêu điểm là F1   3; 0  và đi qua điểm M  1; .  2 3 g) Đi qua hai điểm M (1; 0), N  ;1  . 2  h) Đi qua hai điểm M  4;  3  , N  2 2;3 . Baøi 4. L ập phương trình chính tắc của (E), biết: 3 a) Độ dài trục lớn bằng 10, tâm sai bằng . 5 4 b) Một tiêu điểm là F1(8; 0) và tâm sai bằng . 5 3 c) Một đỉnh là A1 (8; 0) , tâm sai bằng . 4 5 2  d) Đi qua điểm M  2;   và có tâm sai bằng . 3 3  Baøi 5. L ập phương trình chính tắc của (E), biết : a) Tâm O tiêu điểm trên Ox, đi qua M(8, 12) và bán kính qua tiêu điểm trái của M bằng 20. b) Tâm O, một đỉnh trên trục nhỏ là A(0,3) và mỗi tiêu điểm nhìn trục nhỏ dưới 1 góc vuông. x2 y2 HD: a) Gọi (E): 1  a2 b2 64 144  2  1 (1) . 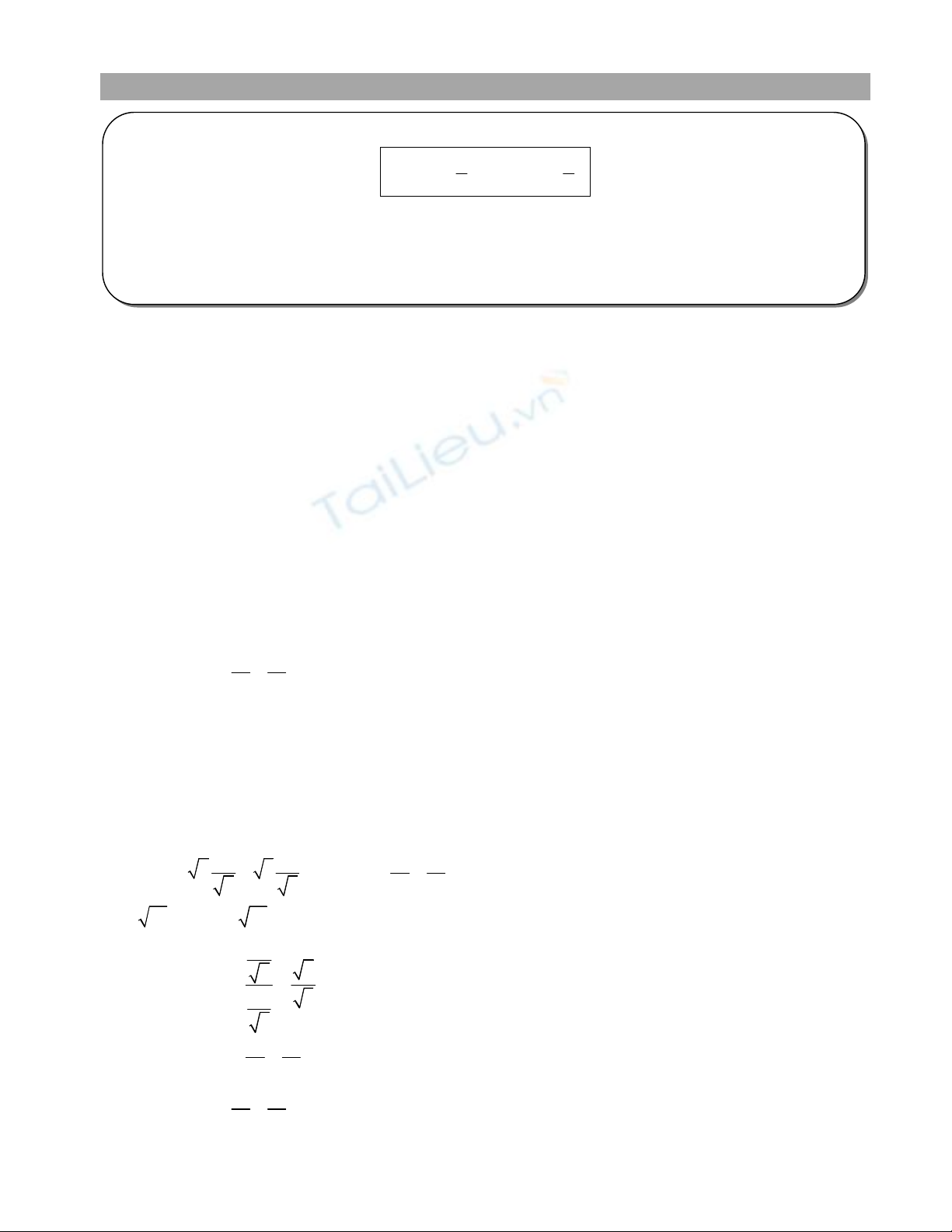Gọi H là hình chiếu M xuống Ox. Ta luôn có MF1 = 20 và tam M thuộc (E) nên : a2 b M giác MHF1 vuông ở H. Tính được HF1 = 16 nên H nằm trong đoạn F1O. Tính được c = HF1+8 (2) 12 Giải (1) và (2) tính được a2 và b2. 8 H F1 O c HTTH 2
NHĐ VẤN ĐỀ 3: TÌM ĐIỂM TRÊN ELIP THỎA ĐIỀU KIỆN CHO TRƯỚC Các công thức xác định độ dài bán kính qua tiêu điểm của điểm M(x; y)  (E): c c MF1  a  x , MF2  a  x a a Nếu điểm phải tìm thỏa mãn điều kiện về góc ta đưa bài toán về hệ thức lượng trong tam giác. Nếu điểm phải tìm là giao của (E) với một đường khác ta xét hệ phương trình tương giao để tìm tọa độ giao điểm. Baøi 6. Cho elip (E) và đường thẳng d vuông góc với trục lớn tại tiêu điểm bên phải F2 cắt (E) tại hai điểm M, N. ii) Tính MF1, MF2 , MN . i) Tìm toạ độ các điểm M, N. a) 9 x 2  25y 2  225 b) 9 x 2  16 y 2  144 c) 7 x 2  16 y 2  112 Baøi 7. Cho elip (E). Tìm những điểm M  (E) sao cho: i) MF1  MF2 ii) MF2  3MF1 iii) MF1  4 MF2 a) 9 x 2  25y 2  225 b) 9 x 2  16 y 2  144 c) 7 x 2  16 y 2  112 Baøi 8. Cho elip (E). Tìm những điểm M  (E) nhìn hai tiêu điểm dưới một góc vuông, với: a) 9 x 2  25y 2  225 b) 9 x 2  16 y 2  144 c) 7 x 2  16 y 2  112 HD : tương giao của (E) với đường tròn tâm là trung điểm F1F2, bán kính là một nửa F1F2 Baøi 9. Cho elip (E). Tìm những điểm M  (E) nhìn hai tiêu điểm dưới một góc 60 0 , với: a) 9 x 2  25y 2  225 b) 9 x 2  16 y 2  144 c) 7 x 2  16 y 2  112 x2 y2   2  8  1 . Tìm những điểm thuộc (E) sao cho : Baøi 10. Cho E : a) Có tọa độ nguyên thuộc (E). b) Có tổng hai tọa độ đạt giá trị nhỏ nhất. HD: a) Do tính đối xứng của (E) qua các trục tọa độ nên nếu M(x,y) thuộc (E) thì các điểm N(-x,- y), P(x,-y), K(-x,y) cũng thuộc (E). Xét phương trình với ẩn y : y 2  8  4 x 2 , phương trình có nghiệm  8  4 x 2  0 . Do x là số nguyên nên x = 1. b) Gọi M(x,y) là điểm thuộc (E). Áp dụng bất đẳng thức Bunhacopxki ta có : 2  x 2 y2  x x  2  x  y    2  8     10 ( do M thuộc (E))  2 8 2 8 2 8    10  x  y  10 x   2 2 Dấu bằng xảy ra  y  8 8  x2 y2 1  2 8 x2 y2  Baøi 11. Cho E :  1 . Tìm các điểm trên (E) sao cho MF1 nhỏ nhất  a2 b2 HD: MF1 = exM+a và a  xM  a HTTH 3
NHĐ VẤN ĐỀ 4 : VỊ TRÍ TƯƠNG ĐỐI ĐƯỜNG THẲNG VÀ (E) Baøi 12. Xét vị trí tương đối đường thẳng d và (E) biết : x2 y2 a) d: x – y – 3 = 0 và  E  : 1  4 1 x2 y2 b) d: 2x + y – 3 = 0 và  E  : 1  9 4 Baøi 13. Cho  E  : 4 x 2  9 y 2  36 . Lập phương trình đường thẳng qua M(1,1) và cắt (E) tại A, B sao cho a) MA = MB. b) AB = 2 VẤN ĐỀ 5 : TAM GIÁC NỘI TIẾP (E) 2 2 x y E :  1 . Xác định tọa độ B, C sao cho tam giác đều ABC nội tiếp (E) biết Baøi 14. Cho  9 3 A(3,0). x 2 y2  Baøi 15. Cho E :  1 và đường thẳng d: 2x +15y -10 =0. Chứng minh rằng (E) luôn cắt d tại  25 4 2 điểm phân biệt A, B. Tìm tọa C thuộc (E) sao cho tam giác ABC cân. VẤN ĐỀ 6 : QUĨ TÍCH Để tìm tập hợp các điểm M(x; y) thoả điều kiện cho trước, ta đưa về một trong các dạng: Dạng 1: MF1  MF2  2a  Tập hợp là elip (E) có hai tiêu điểm F1, F2, trục lớn 2a. x2 y2 Dạng 2:  1 (a > b)  Tập hợp là elip (E) có độ dài trục lớn 2a, trục nhỏ 2b.  a2 b2 Baøi 16. Cho A(6cost,0) và B(0,3sint), t là tham số . Lập phương trình quĩ tích M thỏa :    2 MA  5MB  0 Baøi 17. Cho hai đường tròn C1(F1,R1) và C2(F2,R2), C1 nằm trong C2 v à F1 k hác F2. Gọi M là tâm đường tròn C thay đổi nhưng luôn tiếp xúc ngoài C1 và tiếp xúc trong C2. Chứng tỏ M di động trên (E). Baøi 18. trong mặt phẳng toạ độ cho điểm M(x,y) thỏa mãn x = 5cost, y = 4sint, trong đó t là tham số. Chứng minh rằng M di động trên (E). Baøi 19. Cho đường tròn (C): x 2  y 2  6 x  55  0 và điểm F (3; 0) : 1 a) Tìm tập hợp các tâm M của đường tròn (C) di động luôn đi qua F1 và tiếp xúc với (C). b) Viết phương trình của tập hợp trên. Baøi 20. Cho hai đường tròn (C): x 2  y 2  4 x  32  0 và (C ): x 2  y 2  4 x  0 : a) Chứng minh (C) và (C) tiếp xúc nhau. b) Tìm tập hợp các tâm M của đường tròn (T) di động và tiếp xúc với hai đường tròn trên. c) Viết phương trình của tập hợp đó. Baøi 21. Tìm tập hợp các điểm M có tỉ số các khoảng cách từ đó đến điểm F và đến đường thẳng  bằng e, với: HTTH 4
NHĐ 1 1 a) F (3;0),  : x  12  0, e  b) F (2;0),  : x  8  0, e  2 2 4 3 c) F (4; 0),  : 4 x  25  0, e  d) F (3;0),  : 3 x  25  0, e  5 5 x2 y2  1 . Một góc vuông đỉnh O quay quanh O, có 2 cạnh cắt (E) lần lượt Baøi 22. Cho elip (E):  a2 b2 tại A và B. 1 1 a) Chứng minh rằng không đổi.  OA2 OB 2 b) Tính khoảng cách từ O đến đường thẳng AB. Suy ra đường thẳng AB luôn tiếp xúc với một đường tròn (C) cố định. Tìm phương trình của (C). ab 1 1 1 1 1 1 1  OH  HD: a) b)      2 2 2 2 2 2 2 a2  b2 a b OH OA OB a b HTTH 5