1
Chương 6
THIẾT KẾ LỌC IIR
Một lọc IIR (đáp ứng xung lâu vô hạn) có đáp ứng xung tồn tại mãi mãi trong quá khứ, hiện tại và
tương lai. Về mặt cấu trúc, một lọc IIR là một hệ thống đệ qui, ở đây có một số kết nối từ ngõ ra đến
một điểm bên trong hệ thống để ngõ ra phụ thuộc vào ngõ vào và ngõ ra trước nó. Thật ra, lọc IIR có
thể là đệ qui hoặc không đệ qui (phần 2.6.2), và một lọc đệ qui có thể là loại IIR hoặc FIR. Khi ta nói
một lọc IIR hoặc lọc đệ qui thường có nghĩa như nhau.
Phương trình tín hiệu vào ra của lọc IIR nhân quả (2.21) lặp lại ở đây:
y(n) =
N
1k
k
a
y(n – k) +
M
0k
k
b
x (n – k)
Với ak , bk là những hệ số lọc. Theo lý thuyết, N, M có thể là vô hạn.
Lọc IIR thì hiệu quả hơn lọc FIR trong độ nhạy, đó là một lọc IIR với ít hệ số hơn có thể cho
đáp ứng biên độ tần số bằng với một lọc FIR với nhiều hệ số hơn. Tuy nhiên lọc IIR có hai mặt nhược
điểm.
Chúng có thể không ổn định nếu những hệ số của nó chọn không thích hợp.
Chúng có thể có pha không tuyến tính (phần 5.2) và vì vậy nó không phù hợp cho một số ứng
dụng lọc.
Xét pha tuyến tính ta nên biết rằng hàm truyền H(z) của lọc pha tuyến tính phải thỏa mãn sự
liên hệ
H(z) = z–N H(z–1)
Với z-N trình bày một sự trễ của N mẫu. Sự liên hệ này ngụ ý rằng ở đây có một cực ảo bên ngoài
đường tròn đơn vị với mỗi cực bên trong, ngược lại điều kiện để lọc là ổn định và nhân quả là tất cả
các cực của nó phải nằm bên trong đƣờng tròn đơn vị (phần 4.4.2). Điều này có nghĩa rằng lọc
ổn định và nhân quả không thể có pha tuyến tính. Nếu không yêu cầu nhân quả, lọc IIR có thể có pha
tuyến tính nhưng trong trường hợp này lọc FIR thì thuận lợi hơn
Trong khi thiết kê lọc FIR không có lợi cho bất kỳ phương pháp thiết kế tương tự, thì lọc IIR
là phù hợp từ mặt phẳng tương tự s đến mặt phẳng số z. Vì vậy, phương pháp thiết kế IIR thì giống
như nguyên mẫu tương tự chẳng hạn: Butterworth, Chebyshev, hoặc lọc elliptic. Hai phương pháp
thiết kế là xung bất biến và biến đổi đôi tuyến tính. Bên cạnh đó, IIR có thể được thiết kế bằng phương
pháp đặt cực không như lọc FIR (phần 4.8), hoặc cũng bằng phương pháp bình phương tối thiểu trong
miền số.,
6.1 Một tóm tắt ngắn về lọc Butterworth, Chebyshev và Elliptic.
Với mục đích của việc thiết kế lọc số, sau đây là một tóm tắt ngắn về kiến thức lọc tương tự thông thấp
là cần thiết. Đầu tiên, ta nhìn lại những thông số khác nhau của lọc số (hình 5.9, 5.10, 5.28). Những
thông số này được áp dụng vào lọc tương tự và được ký hiệu lại như p, c, s . Đáp ứng biên độ có
thể diễn tả ở dạng tuyến tính hoặc thang dB với
|)(|log20|)(| 10 adBaHH
. Ví dụ đáp ứng
được chuẩn hóa biên độ là 1 tương ứng với 0 dB,
2/1
ứng với -3 dB. Ta gọi p là tần số cạnh dải
qua, s là tần số cạnh dải dừng, c là tần số cắt (hoặc tần số -3 dB ). Độ gợn sóng dải qua
p
, và
độ gợn sóng dải dừng
s
được liên hệ với sự suy giảm dải qua và dải dừng ở thang dB như
(6.1)
(6.2)
6.1.1 Lọc Butterworth
Lọc Butterworth là lọc tương tự phổ biến nhất. Nó có độ bằng phẳng lớn nhất tại tần số ( = 0) và
tăng đều trong dải qua và dải dừng. Nó không có độ gợn sóng, băng rộng chuyển tiếp thì ngắn (giữa
dải qua và dải dừng) và đáp ứng pha không tuyến tính (Chebyshev và elliptic cũng có đáp ứng pha
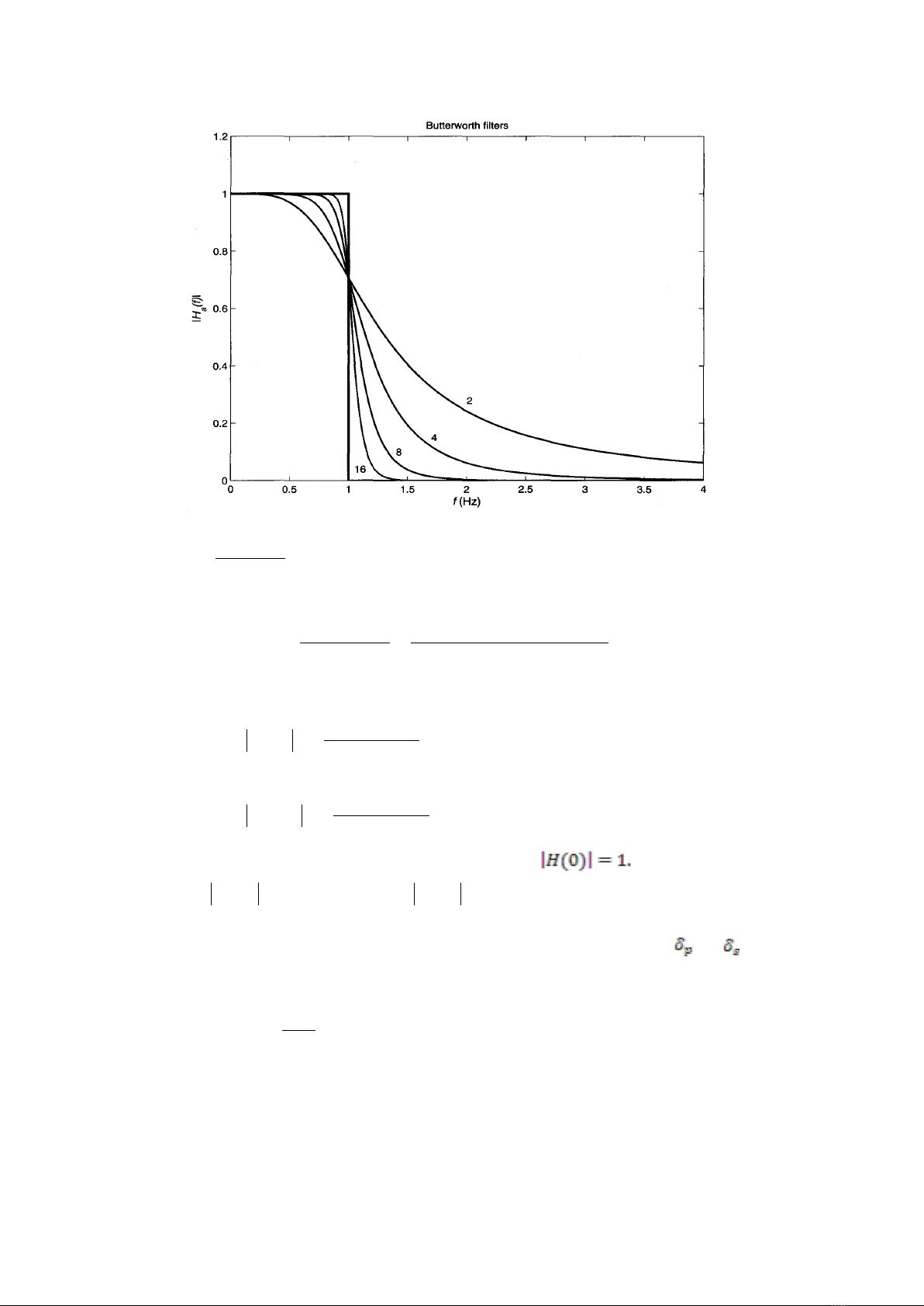
không tuyến tính). Hình 6.1 chỉ đáp ứng biên độ tần số được chuẩn hóa của lọc Butterworth. Bậc lọc
cao hơn gần với đáp ứng lý tưởng.
2
Biểu thức tổng quát của hàm truyền với bậc N của lọc lọc Butterworth là
Ha(s) =
)p)...(sp)(sp(s
1
)p(s
1
a2a1a
ai1i N
N
(6.3)
Hàm có N cực và không có không. Với một lọc thông thấp có hai đối số lọc để thiết kế: Bậc N và tần
số cắt (hoặc -3 dB) c . Bình phương biên độ hàm truyền là
2N
c
2
as/jΩ1
1
(s)H
(6.4)
Bình phương của đáp ứng biên độ tần số có được bằng cách thay s bằng j, mà cho
2N
c
aΩ/Ω1
1
H
2
)(
(6.5)
Chú ý thành phần
trong tử để chắc chắn rằng Những tác giả khác xem đáp
ứng tần số
)(H
thay vì bình phương
2
)(H
.. Điều này đúng cho trường hợp của lọc Chebyshev
và elliptic sẽ được nói đến sau. Lọc Butterworth có độ phẳng lớn nhất vì đáp ứng biên độ của nó bằng
không tại tần số
)0(
. Vì lọc Butterworth không có độ gợn sóng, đối số và được xem là
sự suy giảm.
Những cực của đáp ứng bình phương hàm truyền được cho bởi
1 +
N
c
2
j
s
= 0 s = (–1)1/2N jc
Ta diễn tả -1 và j như thành phần phức:
–1 = ej(2i - 1) i = 1, 2, 3, …
j = ej/2
Vì vậy, những cực là
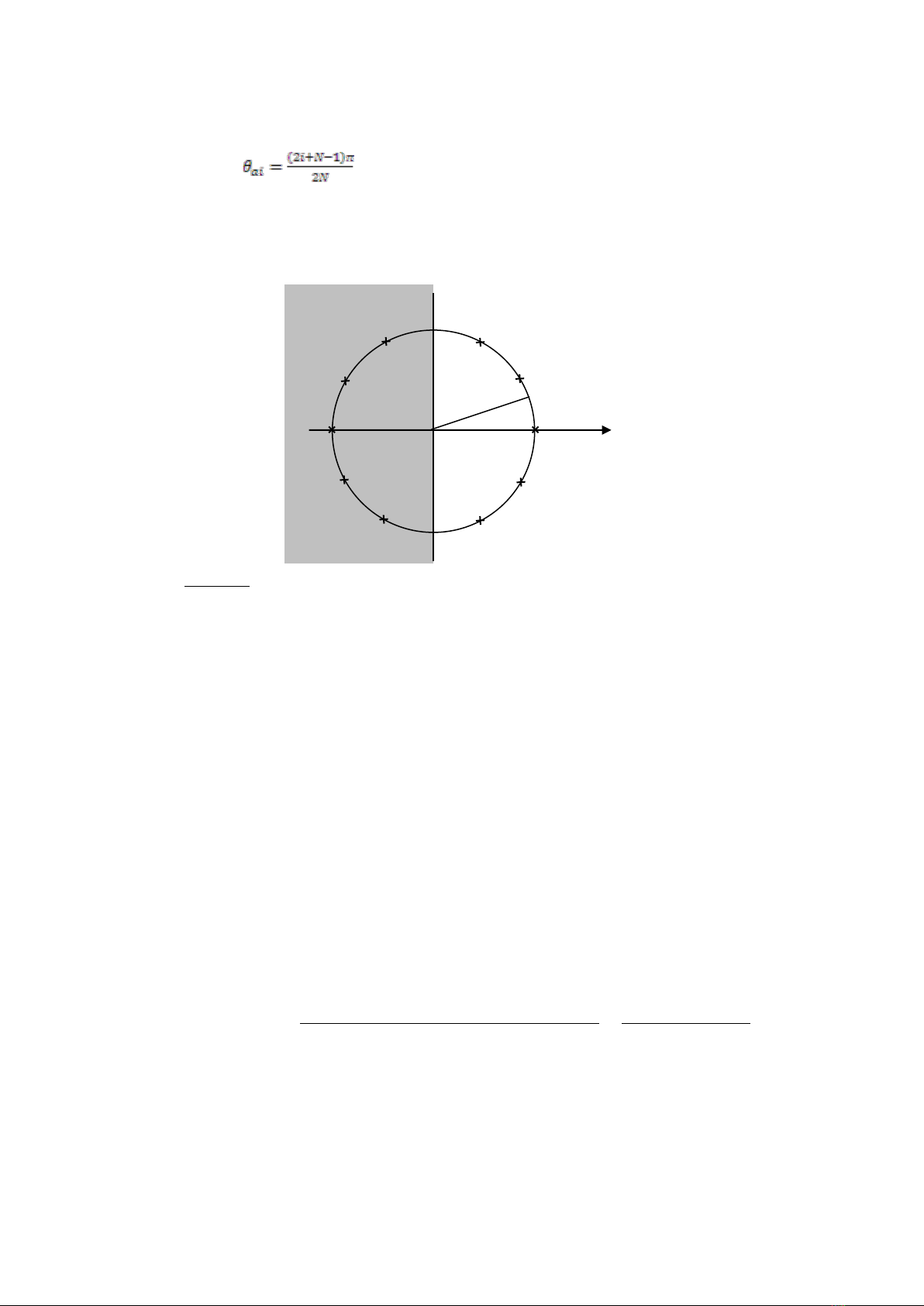
pai = c ej(2i + N - 1)/2N , i = 1, 2, 3, …, 2N (6.6a)
Hình .6.1: Đáp ứng biên độ được chuẩn hóa của lọc Butterworth thông thấp
filters
3
Chú ý rằng độ lớn của tất cả các cực là c và gốc pha là
(6.6b)
Kết quả này chỉ rằng cực được phân bố đều trên một đường tròn có tầm tại gốc và bán kính là tần số
cắt c trong mặt phẳng s (hình. 6.2).
Với lọc có bậc N = 5, số cực là 2N = 10. Cực đầu tiên (i= 1) là
pa1 = c ej(2x1 + 5 - 1)/2x5 = c ej3/5
= c 108O
Cực thứ hai (i = 2) là
pa2 = c ej(2x2 + 5 - 1)/2x5 = c ej4/5
= c 144O
Cực thứ 10 được tách ra bằng 360O/10 = 36O (Hình. 6.2). Để lọc ổn định ta chọn M cực nằm trong nửa
mặt phẳng bên trái, như ví dụ trên là pa1 đến pa5 . Chú ý rằng những cực gồm thực (pa1) hoặc xuất
hiện như đôi liên hiệp phức (pa1 và pa5; pa2 và pa4).
Vì vậy, lọc Butterworth với bậc N có N cực trên mặt phẳng bên trái được cho bởi
pai = c ej(2i + M - 1)/2M i = 1, 2, … N (6.7)
Ví dụ, những cực của lọc bậc ba là
pa1 = c ej2/3 = (–0,5 + j0,866)c
pa2 = c ej = –1c
pa3 = c ej4/3 = (–0,5 - j0,866)c
Vì vậy, với tần số cắt
srad
c/1
hàm truyền là
Ha(s) =
1s2s2s
1
866,0j5,0s1s866,0j5,0s
1
23
Một lọc thông thấp có tần số cắt
srad
c/1
(or
HzFc
2/1
) được gọi là lọc thông thấp chuẩn
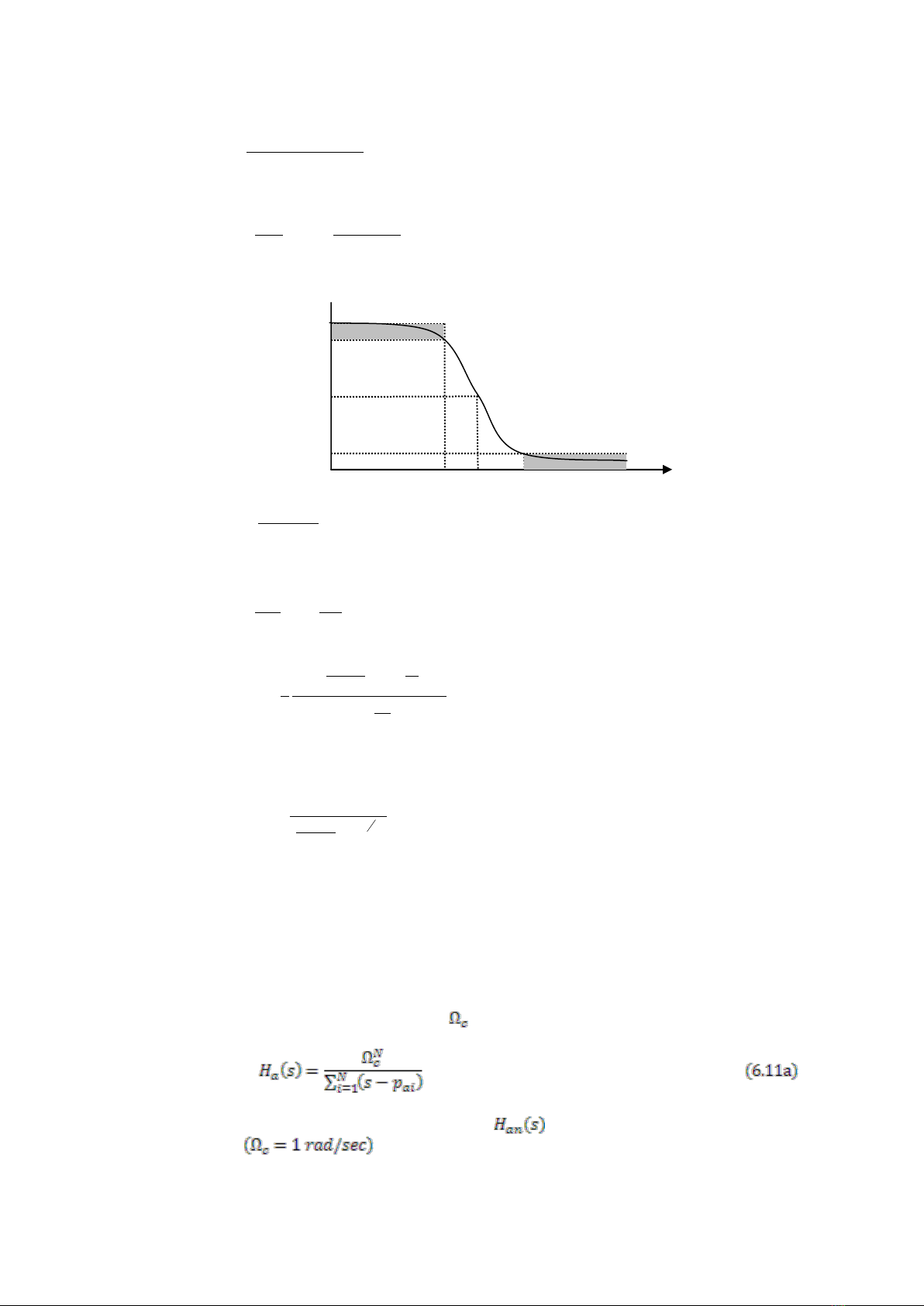
hóa hình 6.3 chỉ đáp ứng biên độ bình phương chuẩn hóa với tần số cạnh dải qua
p
, tần số cạnh dải
dừng
s
, tần số cắt
c
, bình phương độ gợn sóng (sự suy giảm)
2
)1( p
và bình phương độ gợn
sóng dải dừng (sự suy giảm)
2
s
. Từ bình phương đáp ứng biên độ (6.5) ta có thể tìm bậc lọc N để
những đặc tính được gặp nhau. Tạ cạnh dải qua ta có
0
j
s - plane
c
pa1
pa2
pa3
pa4
pa5
pa6
pa7
pa8
pa9
pa10
Hình. 6.2: Cực của
2
|)(| sH a
với N = 5. Cực của lọc Butterworth ổn định
với bậc N = 5 có 5 trong nửa mặt phẳng.
4
2
2)1(
)/(1
1
p
N
cp
or
1
)1(
1
2
2
p
M
c
p
(6.8a)
Giống như vậy, tại cạnh dải dừng ta có
1
1
2
2
s
c
s
(6.8b)
Từ hai biểu thức trước bậc lọc có được
s
p
2
s
2
p
Ω
Ω
δ
1
)δ(1
1
2
1
log
11]/[log
N
(6.9)
Ta lấy N như làm tròn đến một giá trị nguyên gần nhất. Vì vậy đảm bảo rằng dải qua và dải dừng sẽ
quá ngưỡng (tốt hơn yêu cầu)
Để phù hợp những ràng buộc dải qua một cách chính xác ta giải(6.9a) với tần số cắt được cho
N
p
p
c2
1
2]1[ )1(
1
(6.10)
Trong trường hợp này rằng buộc dải dừng sẽ vượt quá và độ gợn sóng dải dừng
s
sẽ nhỏ hơn. Tần số
cắt được cho bởi kết quả trên sẽ lớn hơn giá trị thực có được từ đồ thì của đáp ứng tần số.
Một cách thay thế, giả (6.9b) với tần số cắt
c
để phù hợp chính xác ràng buộc dải dừng
ngược lại điều kiện dải qua sẽ vượt quá. Kết quả này sẽ khác từ (6.11). Nếu ta muốn vượt quá cả điều
kiện dải qua và dải dừng ta sẽ lấy tần số cắt như trung bình của hai tần số cắt được đề cập.
Với những cực được chọn nằm ở nửa bên phải mặt phẳng lọc Butterworth sẽ ổn định. Hàm
truyền của lọc thông thấp bậc N với tần số cắt là
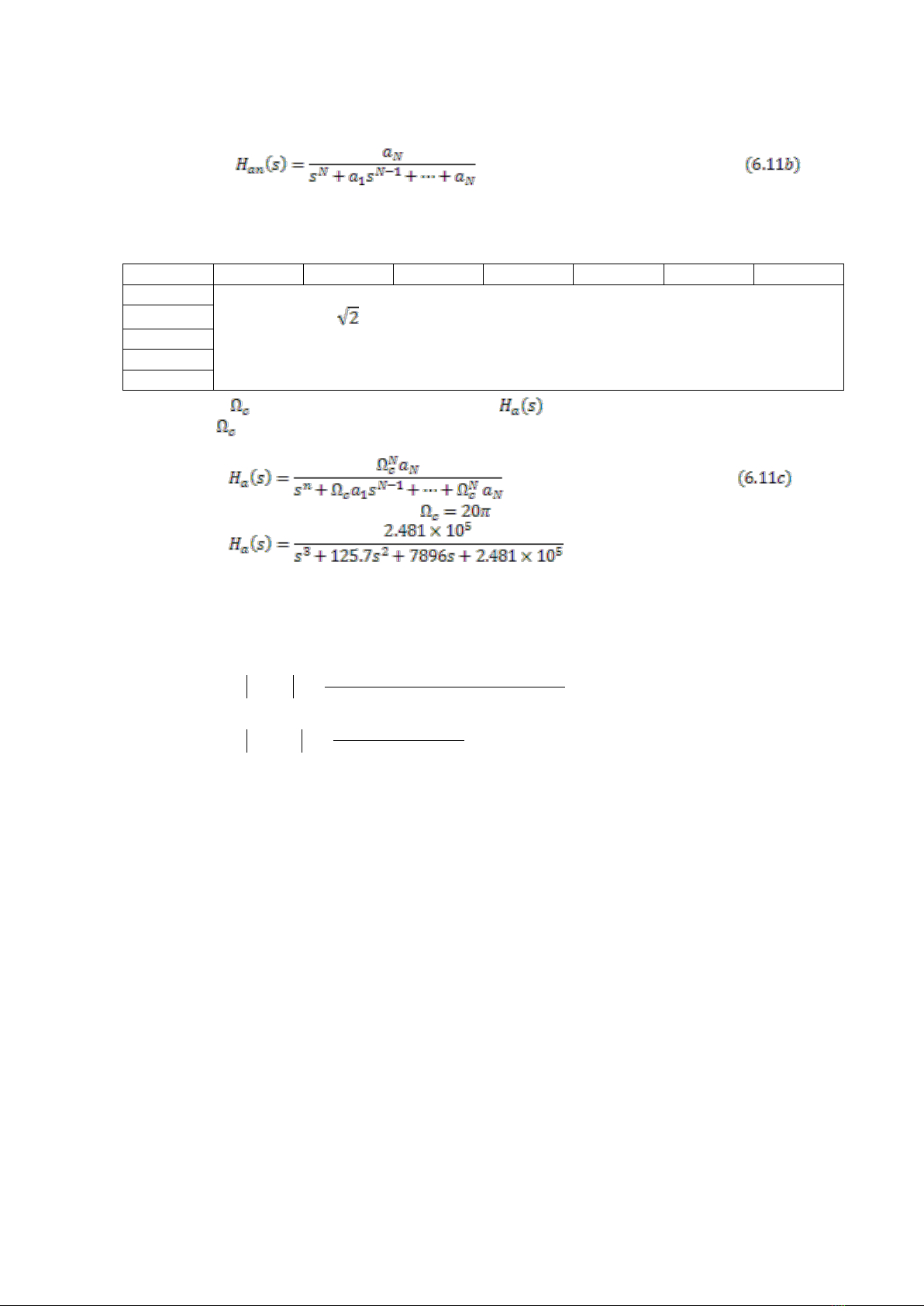
Hàm truyền lọc Butterworth có thể được thiết kế sử dụng (6.6) và (6.11a). Một cách khác ta sử dụng
bẳng những hệ số được tính trước như sau. Chú ý là hàm truyền của lọc thông thấp bậc N
được chuẩn hóa :
Hình 6.3: Bình phương đáp ứng biên độ của lọc Butterworth.
p
0
2
s
)3(5.0 dB
2
)1( p
)0(1 dB
s
2
|)(|
a
H
c
5
Những hệ số của đa tức mẫu với lọc bậc 5 được cho trong bảng 6.1
Bảng 6.1: Những hệ số mẫu của lọc Butterworth thông thấp được chuẩn hóa.
N
a0
a1
a2
a3
a4
a5
a6
1
1
1
0
0
0
0
0
2
1
1
0
0
0
0
3
1
2
2
1
0
0
0
4
1
2.613126
3.414214
2.613126
1
0
0
5
1
3.236068
5.236068
5.236068
3.236068
1
0
Bây giờ, Nếu thực tần số cắt 3-dB, hàm truyền có được bằng cách thay s vào công thức
trên bằng s/ . Đây là sự biến đổi phổ, phần này sẽ được nói đến trong phần 6.4. Vì vậy hàm truyền
lọc Butterworth thông thấp bậc N là
Ví dụ, lọc thông thấp bậc 3 với tần số cắt (nghĩa là , Fc = 10Hz) hàm truyền là
6.1.2 Lọc Chebyshev
Đáp ứng biên độ của lọc Chebyshev (cũng gọi là lọc Cauer) có một độ chuyển tiếp hẹp so với
Butterworth có cùng bậc lọc, và nó gợn sóng (độ gợn sóng giống nhau từ đỉnh này sang đỉnh khac)
trong cùng dải qua hoặc dải dừng (Chebyshev loại 2).
Bình phương của hàm truyền và đáp ứng biên độ tần số của Chebyshev-1 bậc N là
*
cNcN
2
2
as/jΩCs/jΩC 1
1
(s)H
(6.12)
c
2
N
2
2
aΩ/ΩC 1
1
)Ω(H
(6.13)
Với CN(x),
c
x /
, là đa thức Chebyshev-1 của loại đầu tiên của bậc N,
c
là tần số cắt
đối
số độ gợn sóng. Hàm truyền của lọc Chebyshev bậc N cũng có N cực, nhưng không nằm trên đường
trong mặt phẳng s như trong trường hợp của Butterworth nhưng nằm trên ellipse, Biểu thức của đa
thức Chebyshev-1 có bậc không và cao hơn là
CO (x) = 1
C1 (x) = x
C2 (x) = 2x2 – 1
C3 (x) = 4x3 – 3x
C4 (x) = 8x4 – 8x2 + 1
C5 (x) = 16x5 – 20x3 + 5x
CN (x) = 2xCN– 1(x) – CN – 2(x) (6.14)
(6.14) là công thức đệ qui của đa thức.
Hình 6.4 vẽ đáp ứng biên độ bình phương chuẩn hóa của lọc Chebyshev-1 của bậc lẻ. Như ta
thấy, nó gợn sóng trong dải qua và đều trong dải dừng. Tại tần số bằng 0 (
0
) biên độ chuẩn hóa
là 1. Với lọc Chebyshev-1 có bậc chẵn giá trị này là
)1/(12
. Số độ gợn sóng bằng nhau với bậc