1
Chương 7
THỰC HIỆN LỌC VÀ NHỮNG HIỆU ỨNG CHIỀU DÀI TỪ HỮU HẠN.
Thực hiện, cấu trúc, của một lọc số là trình bày phương trình tín hiệu vào ra, hoặc hàm truyền, bằng
giảng đồ (hoặc đồ thị tín hiệu) (phần 1.6.2), sử dụng ba khối cơ bản, cộng, nhân, và đơn vị trễ. Nhưng
để có một lọc đang làm việc, ta phải thiết kế mạch logic (phần cứng) hoặc xử lý phần mềm. Những
cách thực hiện khác nhau trong chương này sẽ trình bày cho cả lọc FIR và IIR.
Mặc khác, hiện thực phần cứng hoặc phần mềm của một lọc từ cấu trúc của nó không thể
chính xác, vì một vài nguồn của lỗi, như lượng tử đầu vào, cắt cụt hoặc làm tròn những hệ số lọc. Vì
vậy, phần hai của chương này thảo luận những hiệu ứng độ dài từ hữu hạn.
7.1 TIẾN HÀNH LỌC FIR
Lọc FIR nhân quả có bậc M có phương trình (công thức 5.2) và hàm truyền (5.4a) tương ứng.
)()(...)2()2()1()1()()0(
)()()(
0
MnxMhnxhnxhnxh
knxkhny
M
k
(7.1)
và
M
zMhzhzhh
zX
zY
zH )(...)2()1()0(
)(
)(
)( 21
(7.2)
Với những hệ số h(n) là đáp ứng xung của lọc. Chú ý rằng một lọc có bậc M có M+1 hệ số.
Ở đây có một vài hình thức khác nhau của sự thực hiện lọc FIR được nói đến như sau
7.1.1 Hình thức trực tiếp
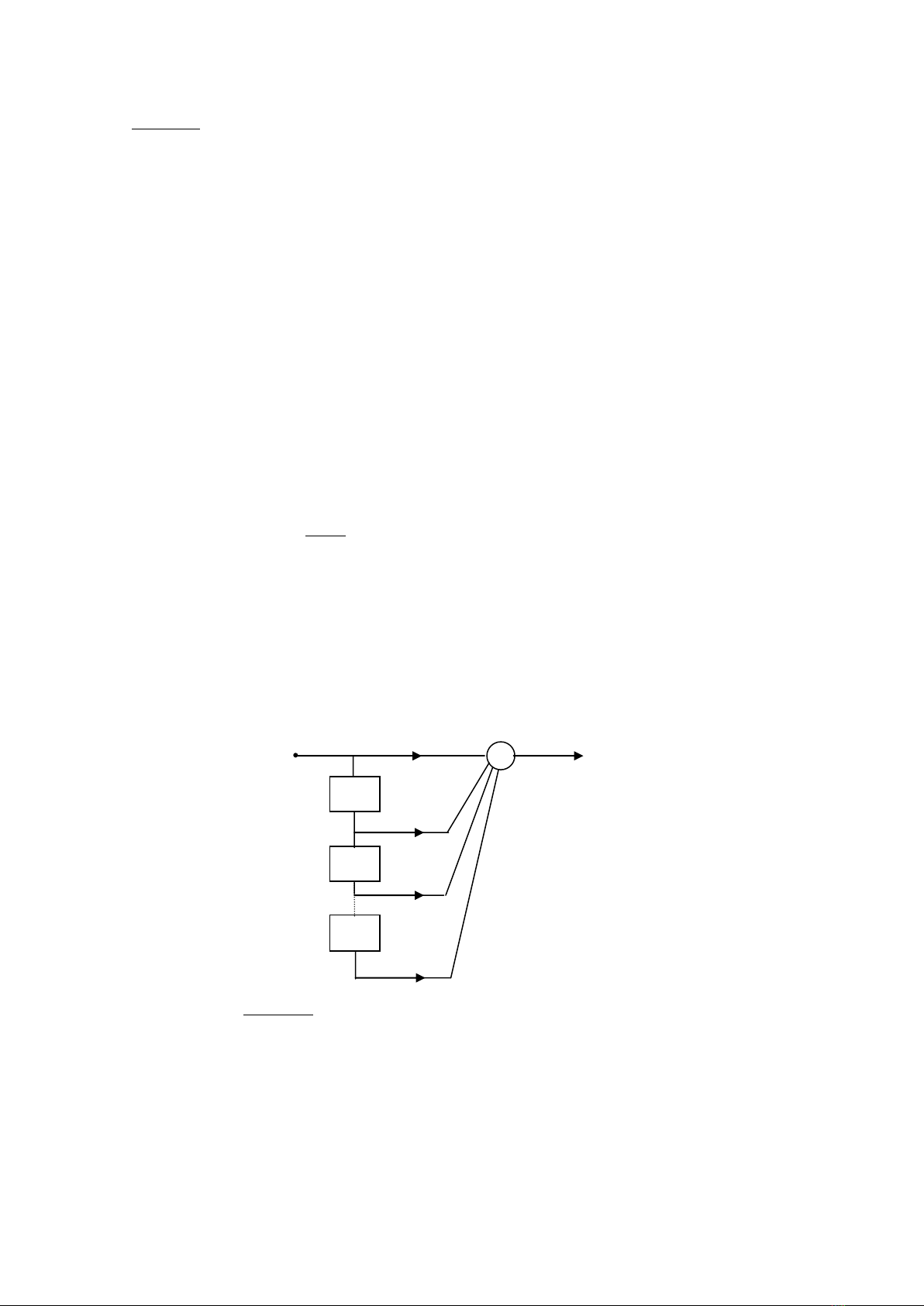
Quan sát công thức trên ta vẽ giản đồ của lọc FIR bậc ba như hình 7.1 được gọi là sự thực hiện hình
theo thức trực tiếp. Hình 7.2 chỉ một hình thức với lọc bậc M có M bộ cộng, và M đơn vị trễ. Vì một
sự nhân tốn nhiều thời gian hơn một bộ cộng, lý tưởng là giảm số nhân càng nhiều càng tốt, nhưng sự
giảm bộ cộng cũng hữu ích.
Hình. 7.1:Cấu trúc của lọc FIR bậc ba
)(nx
)(ny
)1(h
1
z
1
z
+
)2(h
)3(h
)0(h
2
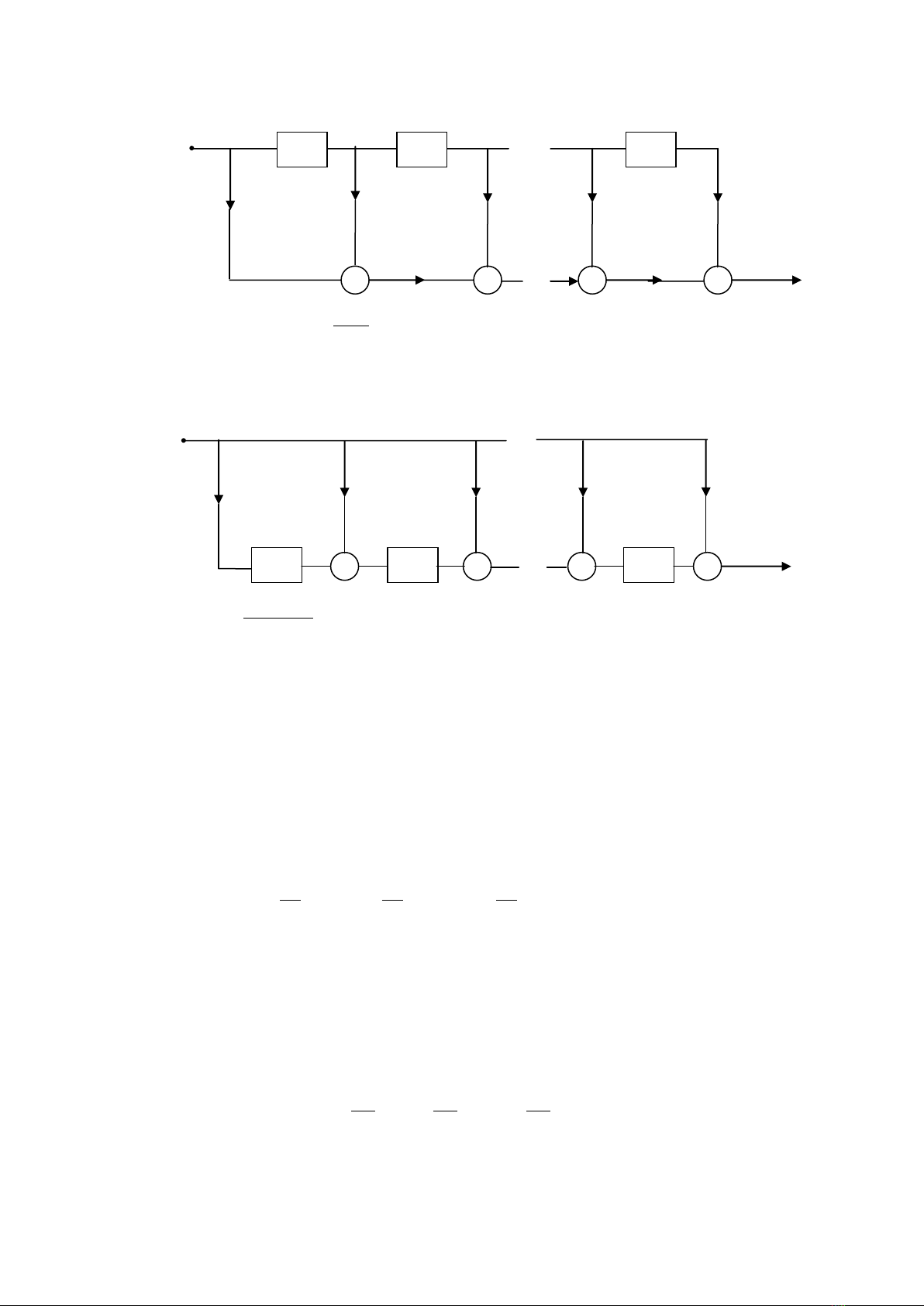
Hình. 7.2: Tapped-đường trễ (đường chuyển)lọc FIR bậc M
Theo lý thuyết chuyển vị, hay định lý đảo ngược, ta có thể di chuyển đơn vị trễ ở đường trên
hình 7.2 xuỗng đường dưới và đảo bậc của những nhánh hệ số như hình 7.3, mà không ảnh hưởng đến
sự quan hệ vào-ra.
Hình. 7.3: Thay đường tapped trễ (đường chuyển tiếp) lọc FIR bậc M.
7.1.2 Cấu trúc pha tuyến tính
Như thảo luận trong chương 6, hầu hết lọc FIR được thiết kế để có pha tuyến tính (bao gồm pha tuyến
tính tổng quát), và ở đây có 4 loại được chú thích như FIR-1 đến FIR-4 (hình 5.5) phụ thuộc bậc lọc M
là chẵn hay lẻ và những hệ số lọc (đáp ứng xung) h(n) là đối xứng hoặc phi đối xứng.
Đầu tiên, xét trường hợp FIR-1, với M chẵn, h(n) đối xứng với hệ số giữa h(M/2), nghĩa là
)()( nMhnh
. Công thức lọc là
)]1
2
()1
2
()[1
2
(
...)]1()1()[1()]()()[0(
)()0()1()1(...)1()1()()0(
)()()1()1(...)1()1()()0()(
M
hx
M
nx
M
h
MnxnxhMnxnxh
MnxhMnxhnxhnxh
MnxMhMnxMhnxhnxhny
(7.3)
Vì vậy nhóm từng đôi với những hệ số bằng nhau, từ thành phần giữa h(M/2) x(n – M/2), số phép
nhân giảm đi một nửa (Hình. 7.4).
Với FIR-2, M là lẻ, M + 1 là chẵn, những hệ số đối xứng, h(n) = h(M – n), và đối xứng là M/2.
Công thức lọc
)]()()[(
)]1()1()[1()()()[0(
)()0()1()1(...)1()1()()0(
)()()1()1(...)1()1()()0()(
2
1
2
1
2
1
MMM nxnxh
MnxnxhMnxnxh
MnxhMnxhnxhnxh
MnxMhMnxMhnxhnxhny
(7.4)
)(Mh
)1( Mh
)2(h
)1(h
)0(h
…
)(nx
+
)1(h
1
z
1
z
1
z
)0(h
+
+
+
)2(h
)1( Mh
)(Mh
)(ny
…
)(nx
+
1
z
+
+
+
)(ny
1
z
…
1
z
…
3
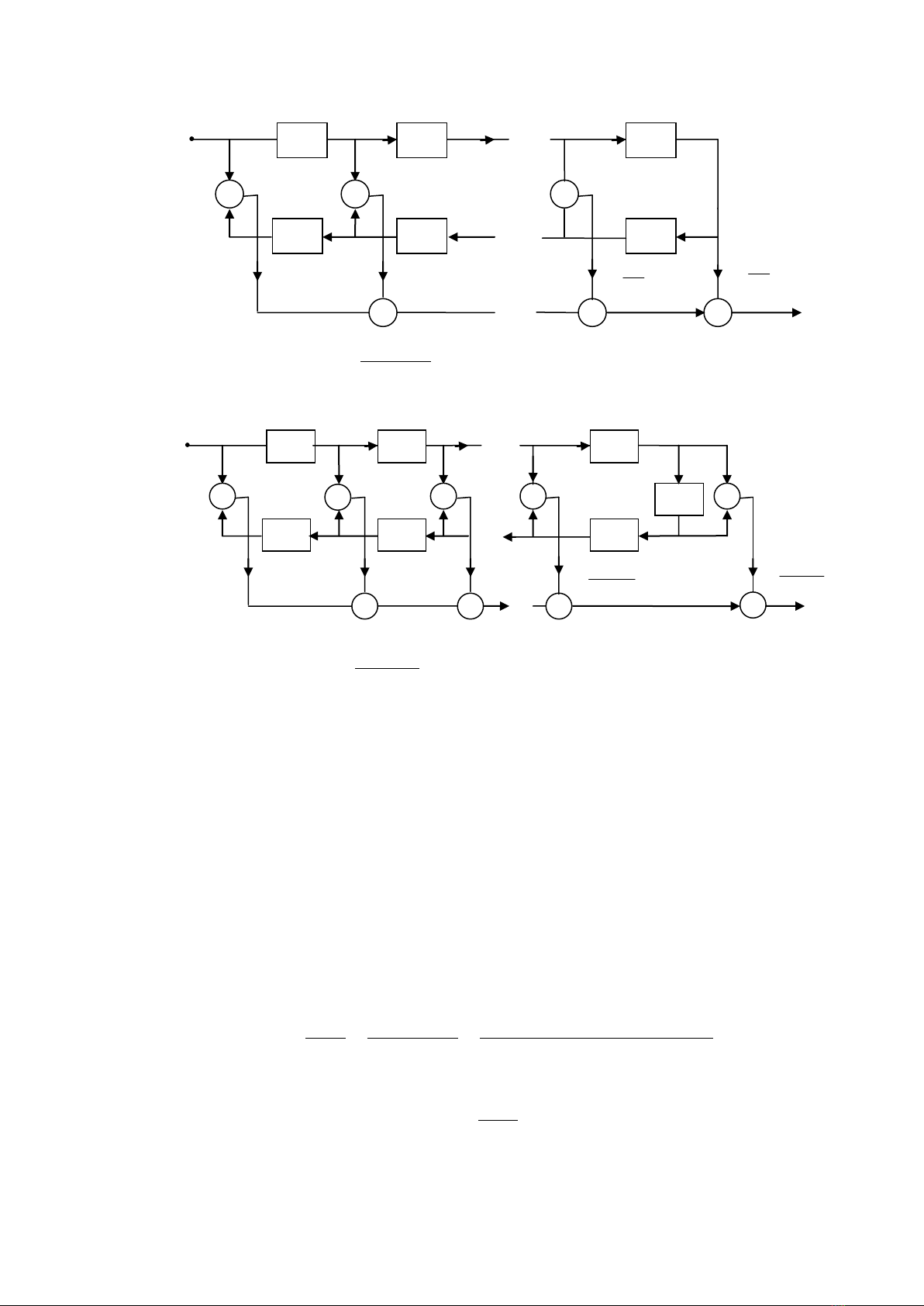
Hình. 7.4: Dạng tực tiếp cho FIR -1
Cấu trúc được chỉ trong hình 7.5.
Hình. 7.5: Dạng trực tiếp với FIR-2
Ta có thể xử lý giống như thế cho FIR-3 và FIR-4.
Lọc FIR có thể có dạng khác gọi là dạng lưới mà sẽ nói kèm với lọc IIR trong phần 7.4.
7.2 THỰC HIỆN LỌC IIR: DẠNG TRỰC TIẾP VÀ DẠNG CHUYỂN VỊ
Phương trình tín hiệu của lọc IIR nhân quả là
M
k
k
N
k
kknxbknyany
01
)()()(
(7.5)
Với bk là những hệ số lọc của phần trước (không đệ qui), và ak là những hệ số của phần hồi tiếp (đệ
qui). Chú ý rằng một số tác giả viết phương trình như
M
k
k
N
k
kknxbknya
00
)()(
(7.6)
Theo cách này những hệ số ak , trừ a0, có dấu ngược với dấu của ak trong(7.4). Ta đánh dấu dạng (7.7)
từ hàm truyền là (4.13a)
N
N
M
M
N
k
k
k
M
k
k
k
zazaza
zbzbzbb
za
zb
zY
zX
zH
...1
...
1
)(
)(
)( 2
2
1
1
2
2
1
10
1
0
)(
)(
zD
zN
(7.7)
Hàm truyền là nghịch đảo và chú thích đa thức tử và mẫu như N(z) và D(z)
……
)(ny
)1(h
+
1
z
+
……
+
)
2
3
(M
h
)(nx
1
z
1
z
1
z
)0(h
+
+
+
1
z
1
z
+
+
)
2
1
(M
h
1
z
+
)2(h
……
)(ny
)(nx
+
)1(h
1
z
1
z
1
z
)0(h
+
+
)1
2
(
M
h
)
2
(M
h
+
+
+
1
z
1
z
1
z
……
……
4
Như ví dụ, xét một lọc IIR bậc hai có những hệ số đệ qui a1 và a2 , và ba hệ số không đệ qui b0
, b1 và b3 , thì
)2()1()()2()1()( 21021 nxbnxbnxbnyanyany
(7.8)
và
2
2
1
1
2
2
1
10
1
)(
zaza
zbzbb
zH
(7.9)
7.2.1 Dạng trực tiếp I
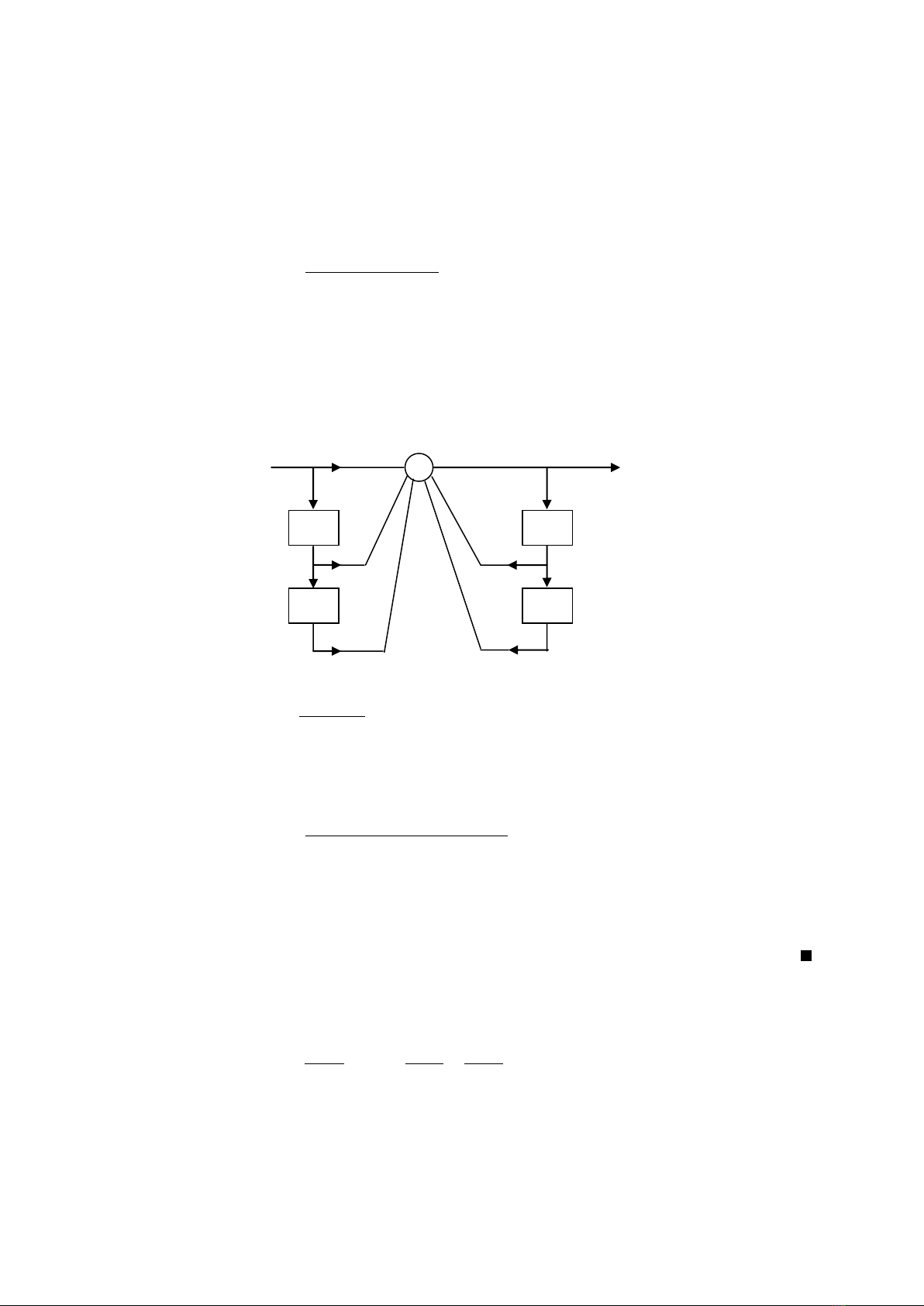
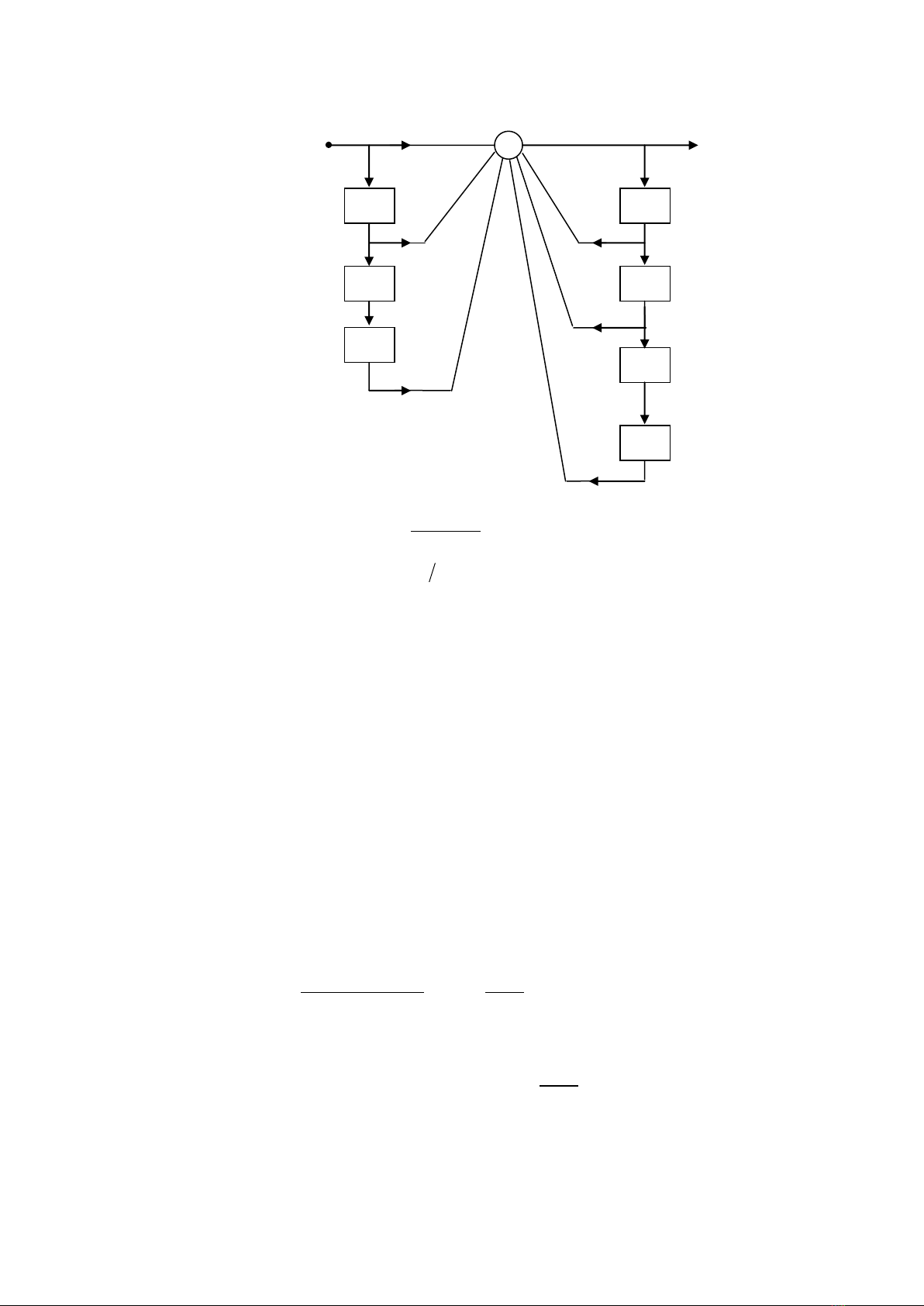
Dạng trực tiếp(hoặc dạng trực tiếp I) là giản đồ trực tiếp trình bày công thức truyền (7.7). Ví dụ với
lọc (7.8) thực hiện dạng trực tiếp là hình 7.6. Chú ý rằng ta có thể tách tổng thành hai tổng nối tiếp,
một cho phần vào và một cho phần ra (xem hình 7.8a).
Hình 7.6: Dạng trực tiếp I của lọc IIR bậc hai (7.9)
Ví dụ 7.2.1
Tìm cấu trúc thực tế của lọc IIR có hàm truyền
421
31
4.05.03.01
543
)(
zzz
zz
zH
Giải
Ta có thể vẽ cấu trúc bằng sự quan sát. Kết quả trong hình 7.7. Phương trình có thể dễ dàng tìm thấy là
)3(5)1(4)(3)4(4.0)2(5.0)1(3.0)( nxnxnxnynynyny
7.2.2 Dạng trực tiếp II (hoặc dạng chính tắc)
Hàm truyền (7.7) có thể được viết như
)(
)(
1
)(
1
)(
)(
)(
)( zN
zDzD
zN
zD
zN
zH
(7.10)
)(nx
1
z
+
1
z
1
z
1
z
)(ny
1
b
2
b
1
a
2
a
0
b
5
Hình. 7.7: Ví dụ 7.2.1
Nghĩa rằng bậc của lọc vào N(z) và lọc ra
)(1 zD
của cấu trúc như hình 7.6 có thể hoán đổi mà không
thay đổi sự quan hệ vào-ra (phương trình vào ra) để có cấu trúc khác. Xét lần nữa lọc bậc hai (7.8).
Dạng trực tiếp với cấu trúc I như hình 7.8a (vẽ lại hình 7.6) với ngõ ra của tầng 1 N(z) đưa đến tầng
ngõ ra 1/D(z). Trong hình 7.8b bậc của hai tầng được đảo ngược, bây giờ tầng vào là 1/D(z) và tầng
ra là N(z). Lấy chú thích tín hiệu trực tiếp là by v(n) thì ta thấy rằng nó bị trễ cùng số mẫu với hai đơn
vị trễ của hai lọc. Hoặc cách nói khác, hai tập trễ có cùng nội dung, vì vậy ta có thể kết nối thành một
tập duy nhất để có cấu trúc hình 7.8c mà là dạng trực tiếp II, cũng gọi là dạng chính tắc với số đơn vị
trễ ít hơn.
Ta có thể kiểm tra cấu trúc bằng cách viết phương trình cho v(n) và y(n):
)2()1()()( 21 nvanvanxnv
)2()1()()( 210 nvbnvbnvbny
Mà trong miền z là
)()()()( 2
2
1
1zVzazVzazXzV
)()()()( 2
2
1
10 zVzbzVzbzVbzY
Giải phương trình với V(z) và Y(z) ta có
)(
)(
1
)(
1
1
)( 2
2
1
1
zX
zD
zX
zaza
zV
)(
)(
1
)(
)()()()()( 2
2
1
10
zX
zD
zN
zVzNzVzbzbbzY
)(nx
1
z
+
1
z
1
z
1
z
)(ny
1
z
1
z
1
z
3
-4
-5
-0.3
0.5
0.4