CH NG TRÌNH LUY N THI ĐI H C C P T C (1 tháng )ƯƠ Ệ Ạ Ọ Ấ Ố
MÔN TOÁN
*Chuyên đ 1 : kh o sát hàm s ề ả ố
S đ chung kh o sát s bi n thiên và v đ th hàm s : 8 b c( 8 d u :+ )ơ ồ ả ự ế ẽ ồ ị ố ướ ấ
I / Hàm s y = axố3 + bx2 + cx + d ( a ≠ 0) .
1) T p xác đnhậ ị : +/ D = R .
2) S bi n thiênự ế :
+/ Chi u bi n thiên : ề ế
y’ = 3ax2 + 2bx + c .
y’ = 0 <=> xi = ? ; f(xi) = ? .
+/ trên các kho ng (….) ảvà (…..) : y’ > 0 , : Hàm s đng bi nố ồ ế .
Trên kho ng (….) : ảy’ < 0 , : Hàm s Ngh ch bi nố ị ế .
+/ C c tr : K t lu n v c c tr hàm s .ự ị ế ậ ề ự ị ố
Hàm s đt c c ti u t i x = …., yố ạ ự ể ạ CT = ….
Hàm s đt c c Đi t i x = …., yố ạ ự ạ ạ CĐ = ….
+ / Gi i h n Vô c c :ớ ạ ở ự
y
x
lim
? ;
y
x
lim
? .
+/ B ng bi n thiên : ả ế
X- ∞ ? ? ? + ∞
y’ ? ? ?
Y ? ? ?
3) Đ th :ồ ị
+ ) Giao đi m đ th v i tr c Oy : x = 0 => y = d .ể ồ ị ớ ụ
Giao đi m đ th v i tr c Ox : y = 0 => x = ? ., Các đi m khác : …ể ồ ị ớ ụ ể
+) Đ th : ồ ị
II / Hàm s y = axố4 + bx2 + c ( a ≠ 0) .
1) T p xác đnhậ ị : +/ D = R .
2) S bi n thiênự ế :
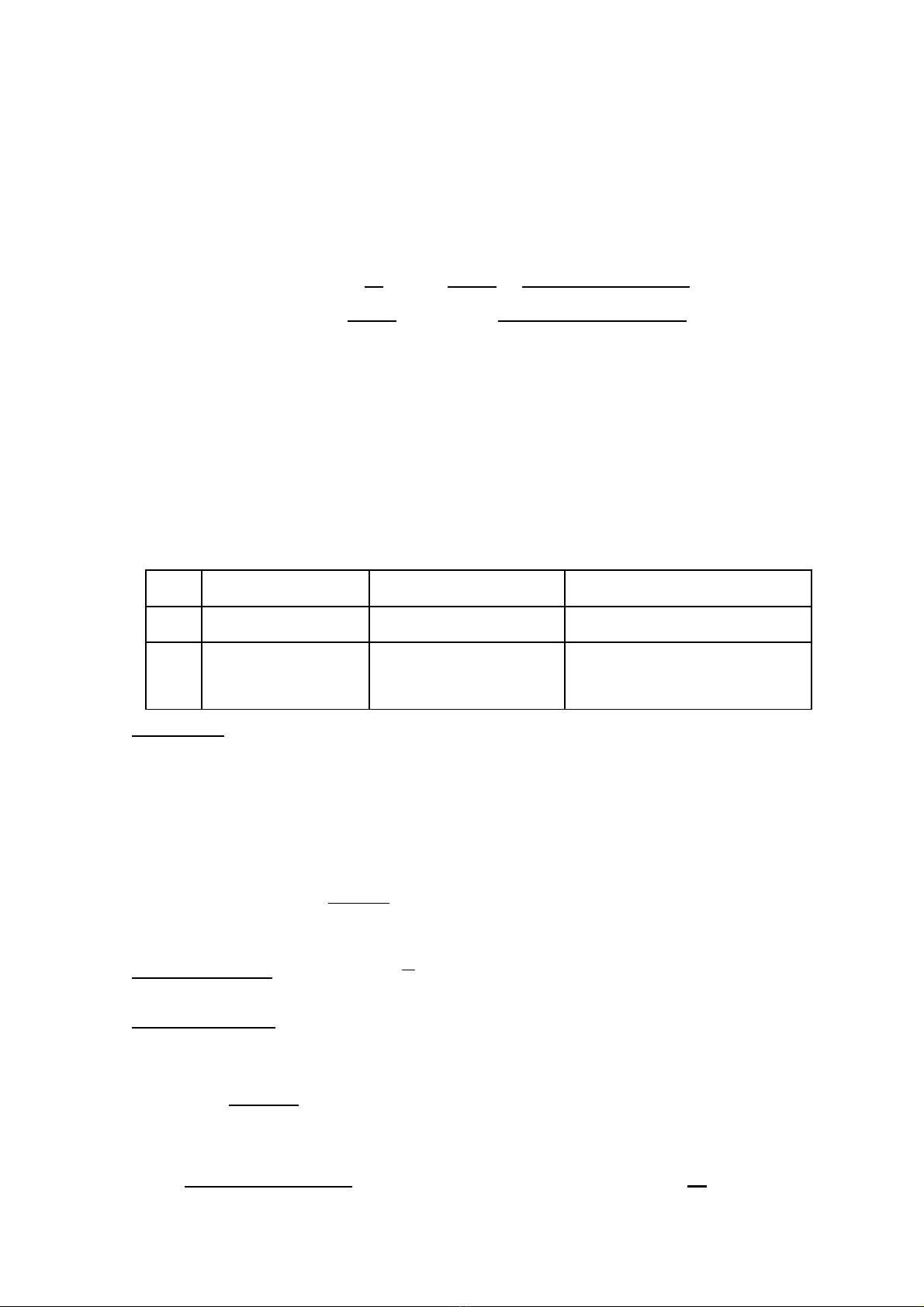
+/ Chi u bi n thiên : ề ế
y’ = 4ax3 + 2bx = 2x(2ax2 + b ) .
y’ = 0 <=>
)(
)(
)0(
?
?
0
xf
xf
cf
x
x
x
.
+/ trên các kho ng (….) ảvà (…..) : y’ > 0 , : Hàm s đng bi nố ồ ế .
Trên kho ng (….) : ảy’ < 0 , : Hàm s Ngh ch bi nố ị ế .
+/ C c tr : K t lu n v c c tr hàm s .ự ị ế ậ ề ự ị ố
Hàm s đt c c ti u t i x = …., yố ạ ự ể ạ CT = ….
Hàm s đt c c đi t i x = …., yố ạ ự ạ ạ CĐ = ….
+ / Gi i h n Vô c c :ớ ạ ở ự
y
x
lim
? ;
y
x
lim
? .
+/ B ng bi n thiên : ả ế
X- ∞ ? ? ? + ∞
y’ ? ? ?
Y ? ? ?
3) Đ th :ồ ị
Hàm s đã cho là hàm s ch n, do đó đ th nh n tr c 0y làm tr c đi ố ố ẵ ồ ị ậ ụ ụ ố
x ng.ứ
Giao đi m đ th v i tr c Ox : y = 0 => x = ? . Các đi m khác …ể ồ ị ớ ụ ể
Đ th : ồ ị
III / Hàm s : ố
dcx
bax
y
1) T p xác đnhậ ị : +/ D = R /{ -
c
d
. }
2) S bi n thiênự ế :
+/ Chi u bi n thiên : ề ế
y’ =
2
)( dcx
bcad
.
y’ > 0 ( y < 0 ) ,
x
D
+/ : Hàm s đng bi nố ồ ế ( Ngh ch bi nị ế ) . trên các kho ng (….) ảvà (…..)
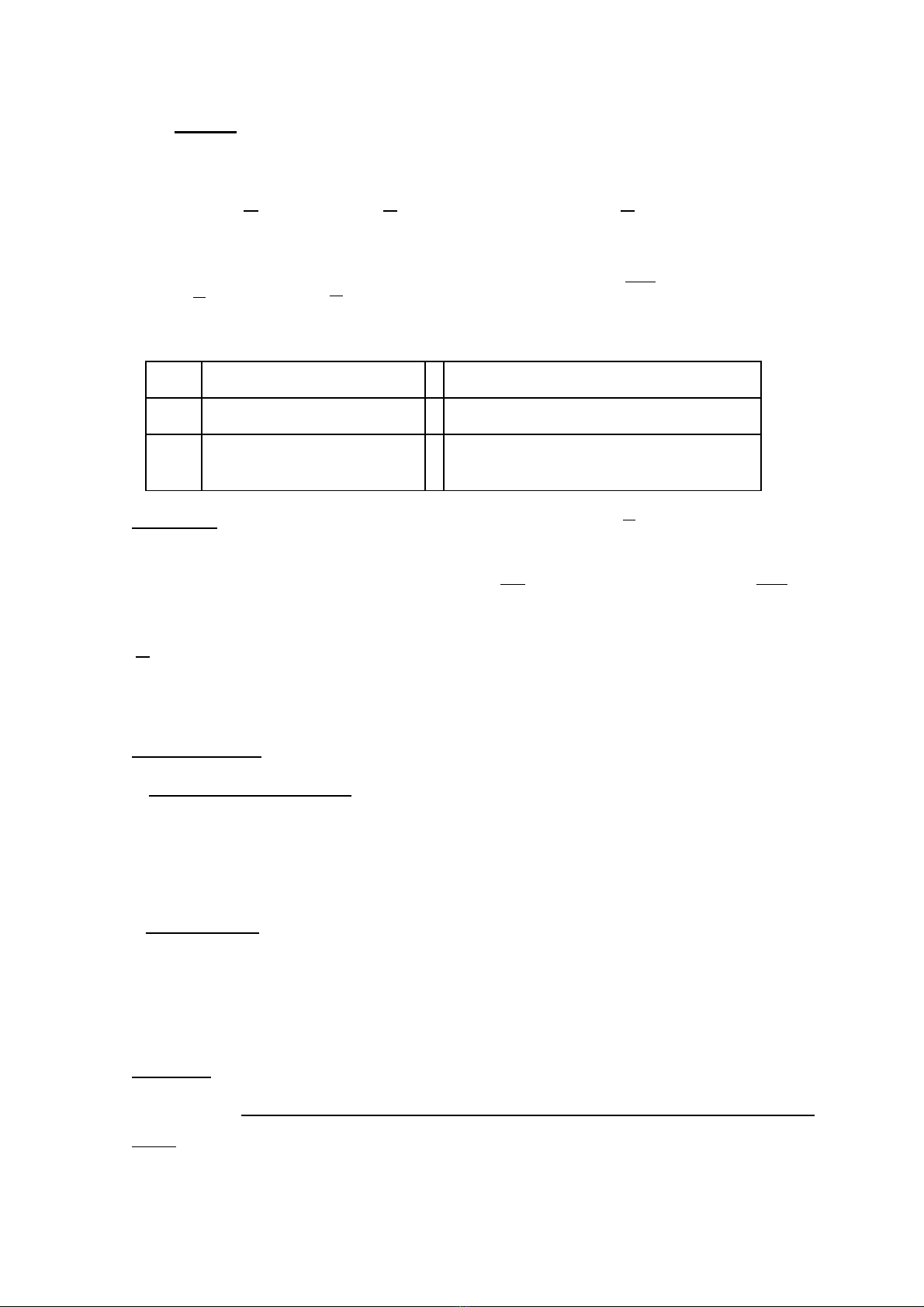
+/ C c trự ị : Hàm s không có c c tr .ố ự ị
+ / Ti m c n và Gi i h n :ệ ậ ớ ạ
y
x
lim
c
a
và
y
x
lim
c
a
=> ti m c n ngang : y = ệ ậ
c
a
.
y
c
a
x
lim
? Và
y
c
a
x
lim
? => ti m c n đng : x = ệ ậ ứ
c
d
.
+/ B ng bi n thiên : ả ế
X- ∞ ? ? + ∞
y’ ? ?
Y ? ?
3) Đ th ồ ị : * Giao đi m đ th v i tr c Oy : x = 0 => y = ể ồ ị ớ ụ
d
b
.
Giao đi m đ th v i tr c Ox : y = 0 => x = ể ồ ị ớ ụ
, Đ th nh n giao đi m I(ồ ị ậ ể
c
d
;
c
a
) c a hai đng ti m c n làm tâm đi x ngủ ườ ệ ậ ố ứ
*Chuyên đ 2 : ềNGUYÊN HÀM , TÍCH PHÂN
A/Nguyên hàm:
I .Đnh nghĩa và ký hi u:ị ệ
1. Đnh nghĩa : F(x) là m t nguyên hàm c a hàm s f(x) n u F’(x) = f(x)ị ộ ủ ố ế
2. Ký hi u: ệ
).().( xFdxxf
3. Đnh lí : ị
).().( xFdxxf
+ C
II. Tính ch t: ấ
1.
dxxf ).('
f(x) +C
2.
dxxfkdxxfk ).(.).(.
3.
dxxgdxxfdxxgxf )()()]()([
Chú ý 1 :
Nguyên hàm d ng tích , và h u t không có công th c ph i bi n đi đa v t ngạ ữ ỷ ứ ả ế ổ ư ề ổ
hi u:ệ
Ví d 1 : Tìm Nguyên hàm : A = ụ
xdxx 5cos.3sin
.
Ví d 2 : Tìm Nguyên hàm : B = ụ
4.3
12
2
xx
x
III .Công th c:ứ
1. Nhóm 1: Hàm s lũy th a.ố ừ
1.1 /
Cxkkdx .
. k
R . 1.2 /
dxx .
=
C
x
1
1
.
1
1.3 /
x
dx
= ln
x
+ C .
2 . Nhóm II: Hàm s l ng giácố ượ
2.1 /
Cxxdx cossin
2.3 /
Cxxdx
coslntan
2.2 /
Cxxdx sincos
2.4 /
Cxxdx
sinlncot
2.5 /
Cx
x
dx
tan
cos
2
2.7 /
Cxx
x
dx
cot
tan
2
2.6 /
Cx
x
dx
cot
sin
2
2.8 /
Cxx
x
dx
tan
cot
2
4. Nhóm III: Hàm s Mũ :ố
3.1 /
C
a
a
dxa
x
x
ln
3.2/
Cedxe
xx
Chú ý 2 :
N u : F(x)’ = f(a) , thì : ế
CbaxF
a
dxbaxf
)(
1
)(
B/ Ph ng pháp tính tích phân:ươ
Công th c : ứ
)()()().( aFbFxFdxxf
b
a
b
a
I/ TÍNH TÍCH PHÂN B NG PH NG PHÁP ĐI BI NẰ ƯƠ Ổ Ế
1. D ng 1ạ: Tính : I
dxxuxuf
b
a
).('.)(
Ph ng pháp chung :ươ
B c 1ướ : Đt : t=u(x) ặ
dt = u’(x).d
B c 2ướ : Đi c n : x a bổ ậ
t u(a) u(b)
B c 3ướ : Tính I :
I =
)]([)]([)()(
)(
)(
)(
)(
auFbuFtFdttf
bu
au
bu
au
CÁC D NG C B N TH NG G P :Ạ Ơ Ả ƯỜ Ặ
2. D ng 2ạ : Tính : I =
b
a
dxxf ).(
; V i f(x)ớ =
).( 1bxax
.
R*
3. Ph ng pháp:ươ
4. B c 1ướ : Đt t = ặ
).(
1
bxa
dt = a
dxx
).1.(
.
a
dt
dxx ).1(
.
5. B c 2ướ : Đi c n : x a bổ ậ
t u(a) u(b)
B c 3ướ : Tính I :
I =
.
).1).(1(
1
).1(
.
)(
)(
)(
)(
)1(
bu
au
bu
au
t
aa
dtt
Ví d 3: Tính các tích phân sau : ụ
1. A =
dxxx
2
1
543 )12(
. ; B =
dx
x
x
2
1
54
3
)12(
.
2. C =
.)12(
2
1
543
dxxx
. ( Ta đt t = ặ
54 )12( x
)
3. D ng 3ạ : Tính : I =
b
a
dxxf ).(
; V i f(x)ớ =
)sin..(cos bxax
.
Ph ng pháp:ươ
B c 1ướ : Đt t = ặ
)sin.( bxa
dt = a
dxx.cos.
.
cosx.dx =
a
dt
.
f(x)dx =
dtt
a
1
. ta đa v bài toán quen thu c. ư ề ộ
Ví d 4 : Tính các tích phân sau : ụ
4 . D =
.)3sin2(cos
3
0
3
dxxx
; 5 . E =
dx
x
x
3
3
0)3sin2(
cos
.