1
CHUYÊN ĐỀ.GIÁ TRỊ MIN-MAX VÀ BẤT ĐẲNG THỨC
A.TRỌNG TÂM CẦN ĐẠT
I. TÓM TẮT LÝ THUYẾT
Vớimọi n
vàmọi
A
tacó: 2
0
n
A
,và 2
0
n
A
khi
0
A
.
Vớimọi
A
tacó:
0
A
,và
0
A
khi
0
A
.
A B
(với
,
A B
cùngdấu)thì
1 1
A B
.
0 0
n
A A
(với
n
làsốtựnhiên).
II. CÁC DẠNG TOÁN
Dạng 1: Tìm GTLN - GTNN của biểu thức chứa lũy thừa với số mũ chẵn.
Với n
,
A
làbiểuthứcchứa
; ;...
x y
và
m
làsốtùyý,ởdạngnàytađưarahailoạibàitoáncơ
bảnnhưsau:
Loại 1: Tìm GTNN của biểu thức dạng: 2
.n
k A m
với
0
k
.
Hướng giải:Với
0
k
vàmọi
A
tacó 2 2 2
0 . 0 .
nnn
A k A k A m m
.
DođóGTNNcủa 2
.n
k A m
là
m
khi
0
A
.
Ví dụ 1: TìmGTNNcủabiểuthức
4
2 5 3
A x
.
Lời giải
Vớimọi
x
tacó
4 4
2 5 0 2 5 3 3
x x
,và
4
2 5 0
x
khi
2 5 0
x
hay
5
2
x
.
VậyGTNNcủabiểuthức
4
2 5 3
A x
là
3
khi
5
2
x
.
Ví dụ 2:Tìmgiátrịnhỏnhấtcủacácbiểuthứcsau:
a)
2
4 1 2019
A x
b)
2020
2021 2 2022
B x
Lời giải
a)Vì
2
4 1 0
x x

nên
2
4 1 2019 2019
x .
Dấubằngxảyrakhi
2
4 1 0 1
x x
Vậygiátrịnhỏnhấtcủabiểuthức
A
bằng2019khi
1
x
.
2
b)Vì
2020 2020
2021 2 0 2021 2 2022 2022
x x x .Dấubằngxảyrakhi
2020
2021 2 0 2
x x
.
Vậygiátrịnhỏnhấtcủa
B
bằng
2022
khi
2
x
.
Ví dụ 3: TìmGTNNcủabiểuthức
2020 30
4 3 25
C x y y
.
Lời giải
Vớimọi
;
x y
tacó
2020
0
x y
,và
2020
0
x y
khi
0
x y
hay
x y
.
Vớimọi
y
tacó
30 30
3 0 4. 3 0
y y
,và
30
3 0
y
khi
3 0
y
hay
3
y
.
Dođóvớimọi
;
x y
tacó:
2020 30 2020 30
4 3 0 4 3 25 25
x y y x y y
hay
25
B
.
Tacó
25
B
khixảyrađồngthời
x y
và
3
y
hay
3
x y
VậyGTNNcủabiểuthức
2020 30
4 3 25
C x y y
là
25
khi
3
x y
.
Ví dụ 4: Tìmgiátrịnhỏnhấtcủabiểuthức:
2 4
1 1 10
A x y
và
2 4
2 4 1 100, 
n n
B x y n
Lời giải
+Tacó:
2
2 4
4
1 0
1 1 10 10
1 
x x A x y
y y
Dấubằngxảyrakhi
2
4
1 0
1
1
1 0
x
x
y
y
.
Vậygiátrịnhỏnhất
10
A
khi
1
1
x
y
+Tacó:
2
2 4
4
2 0
2 4 1 100 100
4 1 0
n
n n
n
x x x y
y y
Dấubằngxảyrakhi
2
4
2 0
2
1
4 1 0
n
n
xx
y
y
.
Vậygiátrịnhỏnhất
100
B
khi
2
1
x
y
.
Ví dụ 5: Tìmgiátrịnhỏnhấtcủabiểuthứcsau:
1 30
A x x x
3
Phân tích:
Vớibàitoánmàbiểuthứcchưacódạng 2
.
A a M b
.Tađặtthừasốchungđểđưavềdạng
2
.
A a M b
Lời giải
Tacó:
2
. 1 1. 1 29 1 1 29 1 29
A x x x x x x
+Vì
2
1 0
x x
nên
2
1 29 29
x
.
Dấubằngxảyrakhi
2
1 0 1
x x
Vậygiátrịnhỏnhấtcủabiểuthức
A
bằng29khi
1
x
.
Loại 2: Tìm GTNN của biểu thức dạng: 2
.n
k A m
với
0
k
.
Hướng giải:Với
0
k
vàmọi
A
tacó 2 2 2
0 . 0 .
nnn
A k A k A m m
.
DođóGTLNcủa 2
.n
k A m
là
m
khi
0
A
.
Ví dụ 1: Tìmgiátrịlớnnhấtcủacácbiểuthứcsau
a)
2
2019
5 10
C x .
b)
2020
100
2 10 2
D x .
Lời giải
a)Vì
2
5 0
x x
nên
2
2019 2019
5 10 10
x .
Dấubằngxảyrakhi
2
5 0 5
x x
Vậygiátrịlớnnhấtcủabiểuthức
C
bằng
2019
10
khi
5
x
.
b)Vì
2020 2020
100 100
2 10 0 2 10 2 2
x x x .
Dấubằngxảyrakhi
2020
2 10 0 10
x x
.
Vậygiátrịlớnnhấtcủa
D
bằng
100
2
khi
10
x
Ví dụ 2: TìmGTLNcủabiểuthức
4 6
2 1 2 3
B x y
.
Lời giải
Tacó:
4 6 4 6
2 1 2 3 3 2 1 2
B x y x y
Vớimọi
x
tacó
4 4
1 0 2 1 0
x x
,và
4
1 0
x
khi
1 0
x
hay
1
x
.
Vớimọi
y
tacó
6
2 0
y
,và
6
2 0
y
khi
2 0
y
hay
2
y
.
4
Dođóvớimọi
;
x y
tacó:
4 6 4 6 4 6
2 1 2 0 2 1 2 0 2 1 2 3 3
x y x y x y
hay
3
B
.
VậyGTLNcủabiểuthức
4 6
2 1 2 3
B x y
là
3
khi
1
x
và
2
y
.
Ví dụ 3: Tìmgiátrịlớnnhấtcủabiểuthức
2 2
2 100 10 2025
C x y
Lời giải
+Tacó:
2
2 2
2
2 0
2 100 10 2025 2025
100 10 0
x x C x y
y y
Dấubằngxảyrakhi
2
2
2 0
2
10
100 10 0
xx
y
y
.
Vậygiátrịlớnnhất
2025
C
khi
2
10
x
y
.
Ví dụ 4: Tìmgiátrịlớnnhấtcủabiểuthức
2 2 100
B x x x
Lời giải
Tacó:
2
2 2 2 4 100 2 2 104 2 104
B x x x x x x
+Vì
2
2 0
x x
nên
2
2 104 104
x .
Dấubằngxảyrakhi
2
2 0 2
x x
.
Vậygiátrịlớnnhấtcủabiểuthức
C
bằng
104
khi
2
x
.
Ví dụ 5: Tìmgiátrịlớnnhấtcủabiểuthức 2 2
2 4 50
D x x y y
Lời giải
Tacó:
2 2
2 2
1 2 2 4 55
 1 1 2 2 2 55
 1 1 2 2 55
 1 2 55
D x x x y y y
x x x y y y
x x y y
x y
Vì
2
2 2
2
1 0
1 2 55 55
2 0
x x x y
y y
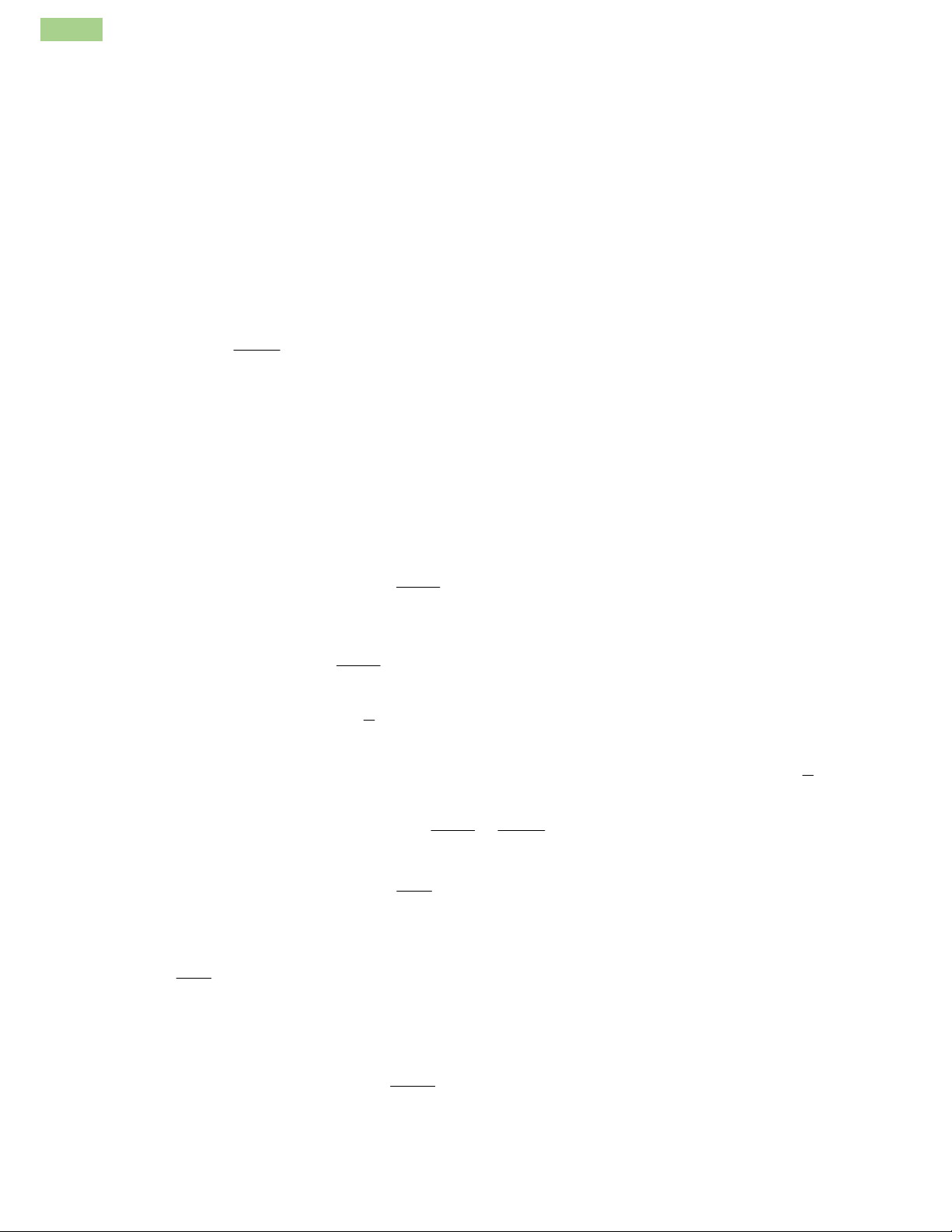
5
Dấubằngxảyrakhi
2
2
1 0
1
2
2 0
xx
y
y
.
Vậygiátrịlớnnhất
55
D
khi
1
2
x
y
.
Dạng 2: Tìm GTLN - GTNN của phân thức.
Ởdạngnàyxétcácbàitoán:Tìmsốnguyên
n
(hoặcsốtựnhiên
n
)đểphânthức
A
cóGTLN–
GTNN.
Loại 1:
.
a
A
b n c
với
; ;
a b c
là các số nguyên đã biết.
+Nếu a
thì:
A
cóGTLNkhi .
b n c
làsốdươngnhỏnhấtứngvới
n
nguyên.
A
cóGTNNkhi .
b n c
làsốâmlớnnhấtứngvới
n
nguyên.
+Nếu a
thì:
A
cóGTLNkhi .
b n c
làsốâmlớnnhấtứngvới
n
nguyên.
A
cóGTNNkhi .
b n c
làsốdươngnhỏnhấtứngvới
n
nguyên.
Ví dụ 1: Tìmsốtựnhiên
n
để
15
2 5
A
n
cóGTLN.TìmGTLNđó.
Lời giải
Tacótửlà
15 0
nên
15
2 5
A
n
cóGTLNkhi
2 5 0
n
vàcóGTNNứngvới n
.
Xét
5
2 5 0 2 5
2
n n n
.
Dođóđể
2 5 0
n
vàcóGTNNứng n
thì
n
phảilàsốtựnhiênnhỏnhấtthỏamãn
5
2
n
.
Từđótasuyra
3
n
vàGTLNcủa
15
2 5
A
n
là 15
15
2.3 5
.
Ví dụ 2:Tìmsốtựnhiên
n
để 5
( 3)
3
P n
n
cógiátrịlớnnhất
Lời giải
Tacó:
5 0
vàkhôngđổi.
3
P
n
cógiátrịlớnnhấtkhi
3
n
làsốnguyêndươngnhỏnhất.
Tacó:
3 0 3
n n
.
Do
n N
và
3
n
làsốnguyêndươngnhỏnhấtsuyra:
4
n
.Khiđó
P
đạtgiátrịlớnnhấtlà
5.
Vậy
4
n
.
Ví dụ 3:Tìmsốnguyên
n
để
7
2 5
P
n
cógiátrịnhỏnhất.
Lời giải