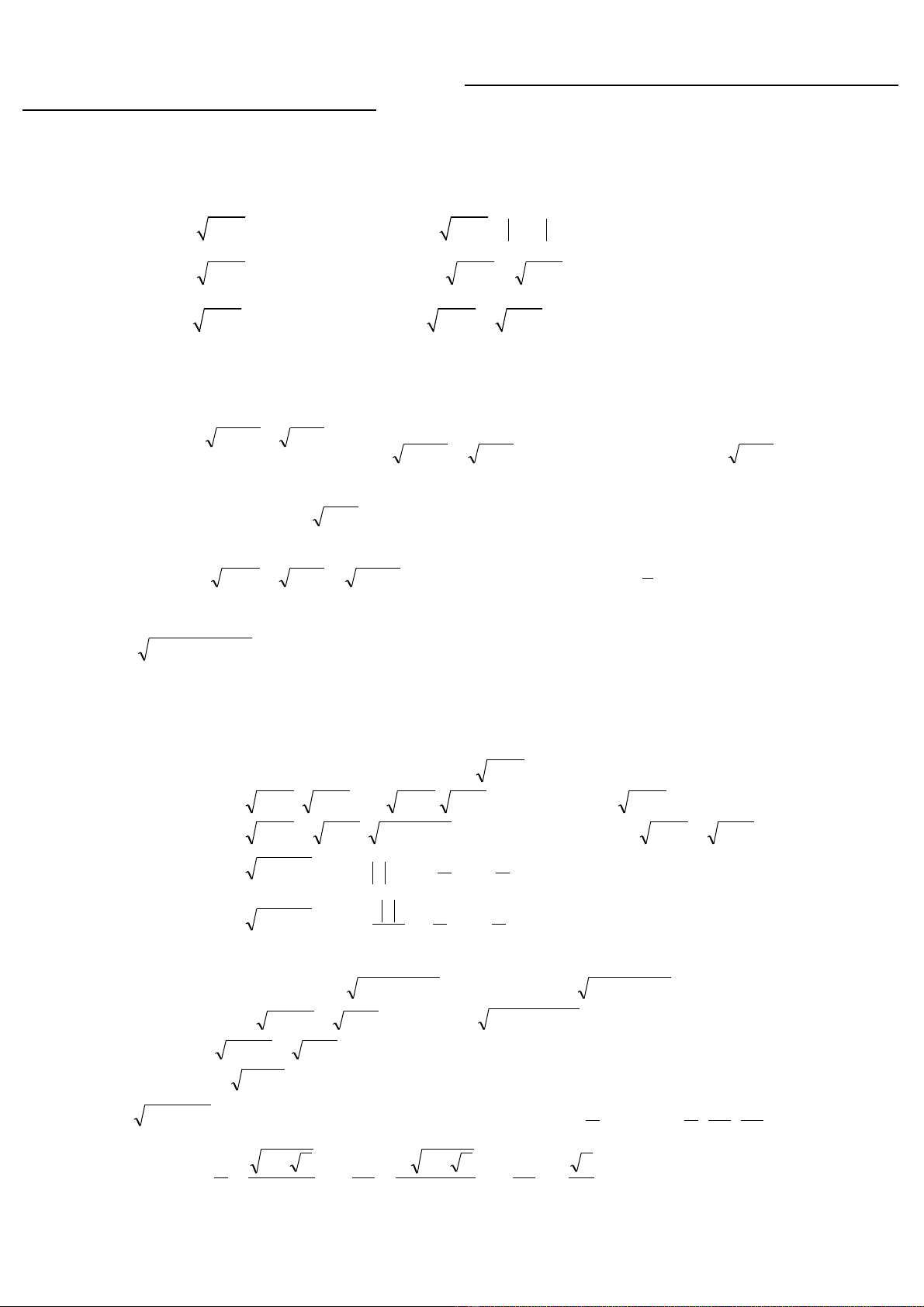
CHUYÊN Đ PH NG TRÌNH, B T PH NG TRÌNH CH A N TRONG CĂNỀ ƯƠ Ấ ƯƠ Ứ Ẩ
PH N I : Ph ng trình có ch a căn (Ầ ươ ứ M I CÔNG TH C HO C M I KĨ THU TỖ Ứ Ặ Ỗ Ậ
CHO 1-2 VD VÀ 1-3 BT T NG TƯƠ Ự)
I)Ph ng pháp bi n đ i t ng đ ngươ ế ổ ươ ươ KĨ THU T: 1.bi n đ i tđ, 2.dùng công th cẬ ế ổ ứ
3.nhân liên h p 4.ợ đ a v tích ….ư ề
1) Ki n th c c b nế ứ ơ ả :
+)
2 2
( ) ( 0) ( ) ; ( ) ( ) ( ) ( )f x a a f x a f x g x f x g x= = = =�� �
+)
=
≥
⇔=
=
≥
⇔= )()(
0)()(
)()(
)()(
0)(
)()( 2xgxf
xghoacxf
xgxf
xgxf
xg
xgxf
+)
3
3 3 3
( ) ( ) ( ) ( ); ( ) ( ) ( ) ( )f x g x f x g x f x g x f x g x= = = =� �
* Chú ý trong các công th c trên thông th ng ứ ườ
( ) & ( )f x g x
là các hàm xác đ nh trên R;ị
các tr ng h p khác ph i tìm đi u ki n xác đ nh tr c khi bi n đ i ườ ợ ả ề ệ ị ướ ế ổ
2) Bài t p áp d ngậ ụ
Bài1: gpt :
2
02012
111
)1(1632464
41
1428
111
144111
111
2111
111
2111
22 =⇔
=+−
≤≤
⇔
−=−+
≤≤
⇔
−=−
≤≤
⇔
−++−=−
≤≤
⇔
+−=−
≤≤
⇔=−−−
x
xx
x
xxx
x
xx
x
xxx
x
xx
x
xx
Bài2: gpt:
xxx 2114 −=−−+
Txđ:
2
1
4
021
01
04
≤≤−⇔
≥=
≥−
≥+
x
x
x
x
1
072
2/12/1
)12()21)(1(
2/1
12)21)(1( 22 =⇔
=+
≤≤−
⇔
+=−−
−≥
⇔+=−−⇔ x
xx
x
xxx
x
xxx
II) Ph ng pháp đ t n ph ươ ặ ẩ ụ KĨ THU T: 1.bi n đ i tđ, 2.dùng công th c 3.nhân liên h pẬ ế ổ ứ ợ
4. đ a v tích ….chú ý…ư ề
1) D ng1: * N u có căn f(x) và f(x) đ t t= ạ ế ặ
)(xf
•N u có ế
taxgxftdatshaxgxfmaxgxf /)()()/()(.)()(,)( =⇒==
•N u có ế
)()(,)()(,)()(,)()( xgxftdataxgxfxgxfxgxf ±==±±
•N u có ế
22
,sin
22
ππ
≤≤−=− ttaxdatxa
•N u có ế
0
22sin
22 ≠≤≤−=−
ππ
t
t
a
xdatax
2) Bài t p áp d ng ậ ụ
Bài1: gpt 2(x2- 2x) +
0632
2=−+− xx
đ t t= ặ
032
2≥+− xx
Bài2; gpt
253294)123(5 2+−+−=−+− xxxxx
đ/k x ≥ 1
đ t t= ặ
123 −+− xx
đ/k t ≥ 1d n t i pt tẫ ớ 2-5t+6=0
Bài3:gpt:
xxx 341 32 −=−
đ/k -1 ≤ x ≤ 1 đ t x = cost ặ
[ ]
π
,0∈t
khi đó pt
2
2
4
3
cos,
2
22
8
5
cos,
2
22
8
cos
4
3
,
8
5
,
8
)
2
cos(3cos3cossincos3cos4cos1 32
−=
−−
=
+
==⇔
=⇔−=⇔=⇔−=−
πππ
ππππ
x
tttttttt
Bài4: gpt:
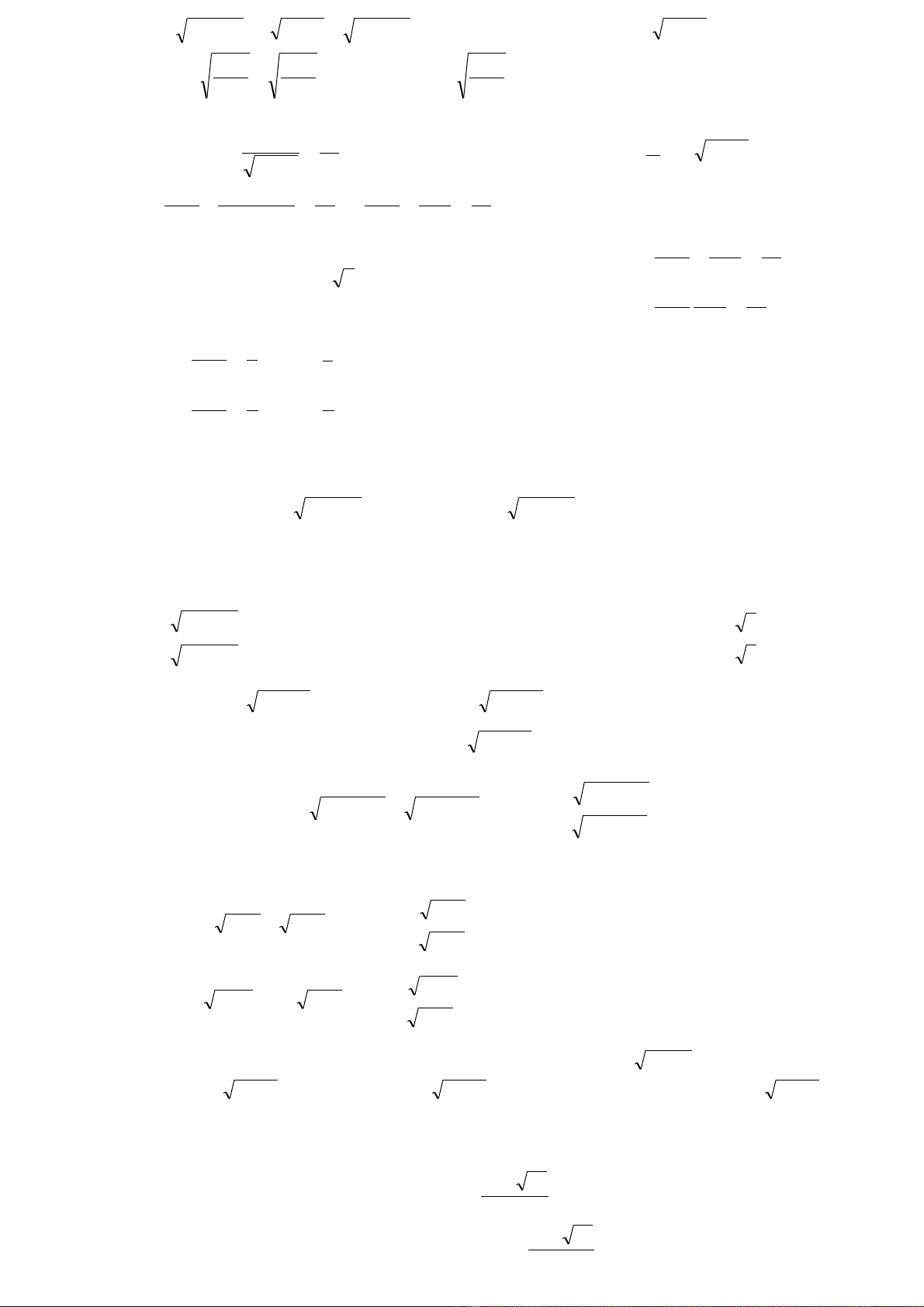
013203/12
1
1
03
1
1
1
1
2
1210)1(13)1(2
2
2222
=+−⇔=−+⇔
−
+
==−
+
−
+
−
+
⇔
−±==−+−−+
tttt
x
x
tdat
x
x
x
x
xvechianglakhongxxxx
gi i ra có t = 1, t = 1/ 2 suy ra nghi m ph ng trình ả ệ ươ
Bài5: gpt :
12
35
1
2=
−
+x
x
x
đ/k x > 1 đ t x = 1/cost ặ
txt tan1)
2
.0(
2
=−⇒∈
π
=
=
⇒
=
=
=
=+
⇔=→=−−⇔∈→+=
=+⇔=+⇔=+⇔
4
5
3
5
4
5
cos
1
3
5
cos
1
12
25
sin
1
cos
1
12
35
sin
1
cos
1
5/70352435)2,1(cossin
cossin35)cos(sin12
12
35
sin
1
cos
1
12
35
cos/sin
cos/1
cos
1
2
x
x
t
t
tt
tt
tuuuttudat
tttt
tttt
t
t
pt
2) D ng2: đ t n ph còn x tham ra nh m t tham s ho c t là tham sạ ặ ẩ ụ ư ộ ố ặ ố
Bài t p áp d ng :ậ ụ
Bài1: gpt
02
0
2
221 222 ≥−=
≤
≥
−=− xxtdat
x
x
dkxxxx
Khi đó pt: x2 -2tx-1 = 0 `= t2+1 = (x-1)2 →x = t±(x-1) khi và ch khiỉ
+=
−=
⇔
=+−
≥
=−−
⇔
−=−
≥−
=−
⇔
−−−=
−+−=
51
51
0123
2/1
012
)12(2
012
12
)1(2
)1(2
2
2
22
2
2
2
x
x
xx
x
xx
xxx
x
xx
xxxx
xxxx
Bài2: gpt (4x-1)
14 2+x
8x2+2x+1 đ t t =ặ
14 2+x
≥ 1 pt : 2t2-(4x-1)t+2x-1=0
Có ngh t=2x-1, t= 1/2(lo i) v i t =2x-1 ạ ớ
−=+
≥
⇔−=+ 22
2
)12(14
2/1
1214 xx
x
xx
vô ngh
3) D ng3: đ t 2 n ph ạ ặ ẩ ụ
=+
+=+
⇒
+=
−=
→=++− cvu
bavu
xfbv
xfau
cxfbxfa
nn
n
n
nn
)(
)(
)()(
Bài t p áp d ng:ậ ụ
Bài1: gpt:
=+
=+
⇒
+=
−=
→=++− 2
2
1
1
211 33
3
3
33
vu
vu
xv
xu
xx
Bài2:gpt:
=
=
=
⇒
−=
=
=
⇒
=+
=+
⇒
−=
−=
→−−=−
10
1
2
2
1
0
1
1
1
2
112
233
3
x
x
x
u
u
u
vu
vu
xv
xu
xx
3) D ng4: m t n ph chuy n ph ng trình thành m t h : ạ ộ ẩ ụ ể ươ ộ ệ
mnxedxcbax +++=+ 2
)(
Thí d : gpt ụ
13324)32(13513413 22 +=+−+++−−=+⇒−+−=+ xydatxxxxxx
−=
=
⇒
+=+−
++=+−
⇔
+=+−
+++−−=+−
⇔xy
yx
xy
yxy
xy
xxy
252
13)32(
12)32(
13)32(
4)32(32
2
2
2
2
8
7311
03114252)2
8
9715
08154)1
2
2
−
=⇒=+−⇒−=
−
=⇒=+−⇒=
xxxxy
xxxyx

III) Ph ng pháp đánh giá ươ
1) Ki n th c c b n: ế ứ ơ ả
1) f2(x) + g2(x) + t2(x) = 0
=
=
=
⇔
0)(
0)(
0)(
xt
xg
xf
2) f(x) + g(x) = a ( a là h ng s )ằ ố
mà f(x) ≤ b , g(x) ≤ c (b + c =a )
=
=
⇔cxg
bxf
)(
)(
3) f(x) = g(x) , f(x) ≤ a, g(x) ≥ a
=
=
⇔axg
axf
)(
)(
2) Bài t p áp d ngậ ụ :
Bài1: gpt x4 + 2x2 -6x +20 =
1622 22 +− xxx
⇔
x4 -
1622 22 +− xxx
+ x2 -2x +16+
x2-4x+4 = 0
⇔
( x2-
162
2+− xx
)2 + ( x-2)2 = 0
⇔
=−
=+−−
02
0162
22
x
xxx
⇔
x = 2 th a mãn h , v y ph ng trình có 1 nghi m x = 2ỏ ệ ậ ươ ệ
Bài2: gpt: 4x2 + 3x +3 = 4x
1223 −++ xx
đ/k x ≥ 1/2 ph ng trình t ng đ ngươ ươ ươ
=−
=+
⇔=−−++− 112
23
0)121()32( 2
2
x
xx
xxx
Bài: gpt:
14105763 22 +++++ xxxx
= 4 – 2x – x2
Ta có vé trái
5949)1(54)1(3 22 =+≥+++++ xx
V ph i 4 – 2x—xế ả 2 = 5 – (x+1)2 ≤ 5 v y ph ng trình ch th a mãn khi c 2 vậ ươ ỉ ỏ ả ế
đ ng th i b ng 5 khi và ch khi x = - 1 là nghi m c a ph ng trình ồ ờ ằ ỉ ệ ủ ươ
IV) Ph ng pháp s d ng tính đ n đi u hàm sươ ử ụ ơ ệ ố
: 1) C s lý thuy tơ ở ế
dùng tính đ n đi u hàm s t đó kh ng đ nh s nghi m ph ng trìnhơ ệ ố ừ ẳ ị ố ệ ươ
2) Bài t p áp d ng ậ ụ
Bài1
2/111414 2≥=−+− dkxxx
xét hàm s y= ố
2/11414 2≥−+− xtxdxx
Có đ o hàm ạ
2/10
14
4
14
2
2
,≥∀>
−
+
−
=x
x
x
x
y
hàm s luôn đ ng bi n trên txđ v y pt khôngố ồ ế ậ
có
quá m t nghi m nh m nghi m ta th y x=1/2 là nghi m duy nh t ộ ệ ẩ ệ ấ ệ ấ
Bài2: gpt
0431
35 =+−−+ xxx
xét hàm s y= ố
431
35 +−−+ xxx
txđ x≤1/3
0
312
3
35 24` >
−
++= x
xxy
h/s đ ng bi n trên txđ v y ph ng trình không có quá ồ ế ậ ươ
m t nghi mTa th y x= -1 là nghi m duy nh t c a bài toán ộ ệ ấ ệ ấ ủ
Bài3:gpt;
⇔=−+−+− 123 22 xxxx
123 22 +−+=+− xxxx
đ t t = xặ2- x đ/k -3≤t≤2
h/s f(t) =
t+3
txđ
[ ]
2,3−
f`(t)=
o
t>
+32
1
hàm s tăng ,ố
g(t) = 1+
0
22
1
)(2 ,<
−
−=⇒− t
tgt
hàm s ngh ch bi n v y chúng ch có th giao nhau t iố ị ế ậ ỉ ể ạ
m t ộ
đi m duy nh t , th y t =1 là nghi m do đó t=1 suy ra pt xể ấ ấ ệ 2- x =1 có nghi m ệ
2
51±
=x
V) Ph ng pháp s d ng tính liên t c hàm s đ ch ng minh s nghi m ph ng trình ươ ử ụ ụ ố ể ứ ố ệ ươ

Bài t p áp d ngậ ụ : CMR ph ng trình sau có 3 nghi m phân bi t thu c (-7,9): ươ ệ ệ ộ
3162 3=−+ xx
đ t t= ặ
31x−
có pt 2t3 – 6t + 1 =0 hàm s này liên t c trên R ,có f(-2)f(0)<0 có 1ngh t thu cố ụ ộ
(-2,0) suy ra có 1 ngh x thu c (1,9) , f(0)f(1)<0 có 1ngh t thu c (0,1) suy ra có 1ngh xộ ộ
thu c(0,1) , ộ
f(1)f(2)< 0 có 1ngh t thu c(1,2) suy ra có 1 ngh x thu c (-7,0) v y ph ng trình đã cho cóộ ộ ậ ươ
đúng 3
nghi m phân bi t thu c ( -7,9)ệ ệ ộ
VI) Ph ng pháp s d ng đ o hàm b c 2ươ ử ụ ạ ậ
* Tìm t p xác đ nh c a ph ng trìnhậ ị ủ ươ
* Xét hàm s f trên mi n D ,t n t i đ o hàm b c 2 suy ra hàm s l i ho c lõm trên mi n Dố ề ồ ạ ạ ậ ố ồ ặ ề
Suy ra ph ng trình không có quá 2 nghi mươ ệ
nh m 2 nghi m thu c mi n Dẩ ệ ộ ề
Bài t p áp d ngậ ụ :
Bài1: gpt :
⇔+−=+ 38313 2xxx
đ/k x≥ - 1 PT t ng đ ng ươ ươ
038313 2=−+−+ xxx
xét hàm s f(x) = ố
38313 2−+−+ xxx
trên t p x/đ x ≥ -1ậ
06
)1(4
3
)(86
12
3
)( 2
,``,, <−
+
−=⇒+−
+
=x
xfx
x
xf
v y hàm s đó có đ th l i trên txđậ ố ồ ị ồ
Do đó ph ng trình n u có nghi m thì không quá 2 nghi m ta d th y x = 0, x = 3 là nghi mươ ế ệ ệ ễ ấ ệ
Bài2;gpt:
113 2++=++ xxxx
đi u ki n x ≥ 0 ph ong trình t ng đ ng v iề ệ ư ươ ươ ớ
0113 2=−−−++ xxxx
xét hàm s f(x) = ố
113 2−−−++ xxxx
t p xác đ nh x ≥ 0 ậ ị
02
)13(4
9
4
1
)(12
132
3
2
1
)( 22
,,, <−
+
−−=⇒−−
+
+= xx
xfx
xx
xf
đ th hàm s l i trên t p xácồ ị ố ồ ạ
đ nh vì v y ph ng trình không có quá 2 nghi m ,d th y x = 0 ,x = 1 là nghi m ị ậ ươ ệ ễ ấ ệ
VII) M t s ph ng trình không m u m cộ ố ươ ẫ ự
Bài1: gpt:
4
3
10
2
6=
−
+
−tt
đ/k x < 2 đ t ặ
22
6
13
6
20
2
6
t
x
t
x
x
t+=−⇔=−⇒>
−
=
Pt thành t+
−=
+
≤
⇔=
+2
2
2
2
2
)4(
6
10
4
4
6
10
t
t
t
t
t
t
khi đócó PT: t4-8t3+12t2-48t+96=0 suy ra
(t-2)(t3-6t2-48)=0 Có nghi m t=2 suy ra x=1/2 cònph ng trình: tệ ươ 3-6t2-48=t2(t-6) -48 <
0 v i o<t≤ 4 vô nghi m, v y pt đã cho có 1 nghi m x=1/2ớ ệ ậ ệ
Bài2: gpt:
431532373 2222 +−−−−=−−+− xxxxxxx
t ong đ ng v iư ươ ớ
432153373 2222 +−−−=−−−+− xxxxxxx
t ng đ ng v i ươ ươ ớ
432
63
153373
42
2222 +−+−
−
=
−−++−
+−
xxx
x
xxxx
x
*) v i m i x > 2 không th là nghi m vì v trái < 0,v ph i > 0 ớ ọ ể ệ ế ế ả
*) v i m i x < 0 cũng không th là nghi mớ ọ ể ệ
*) v i x = 2 là nghi m v y ph ng trình ch có nghi m x = 2ớ ệ ậ ươ ỉ ệ
Bài3: gpt :
x
x
x
x
xx 21
21
21
21
2121 −
+
+
+
−
=++−
đi u ki n - 1/2<x< ½ề ệ
Xét v ph i theo b t đ ng th c cô si ta có ế ả ấ ẳ ứ
2
21
21
21
21 ≥
−
+
+
+
−
x
x
x
x
d u b ng xâ ra khiấ ằ ỷ
0
21
21
21
21 =⇔
−
+
=
+
−x
x
x
x
x
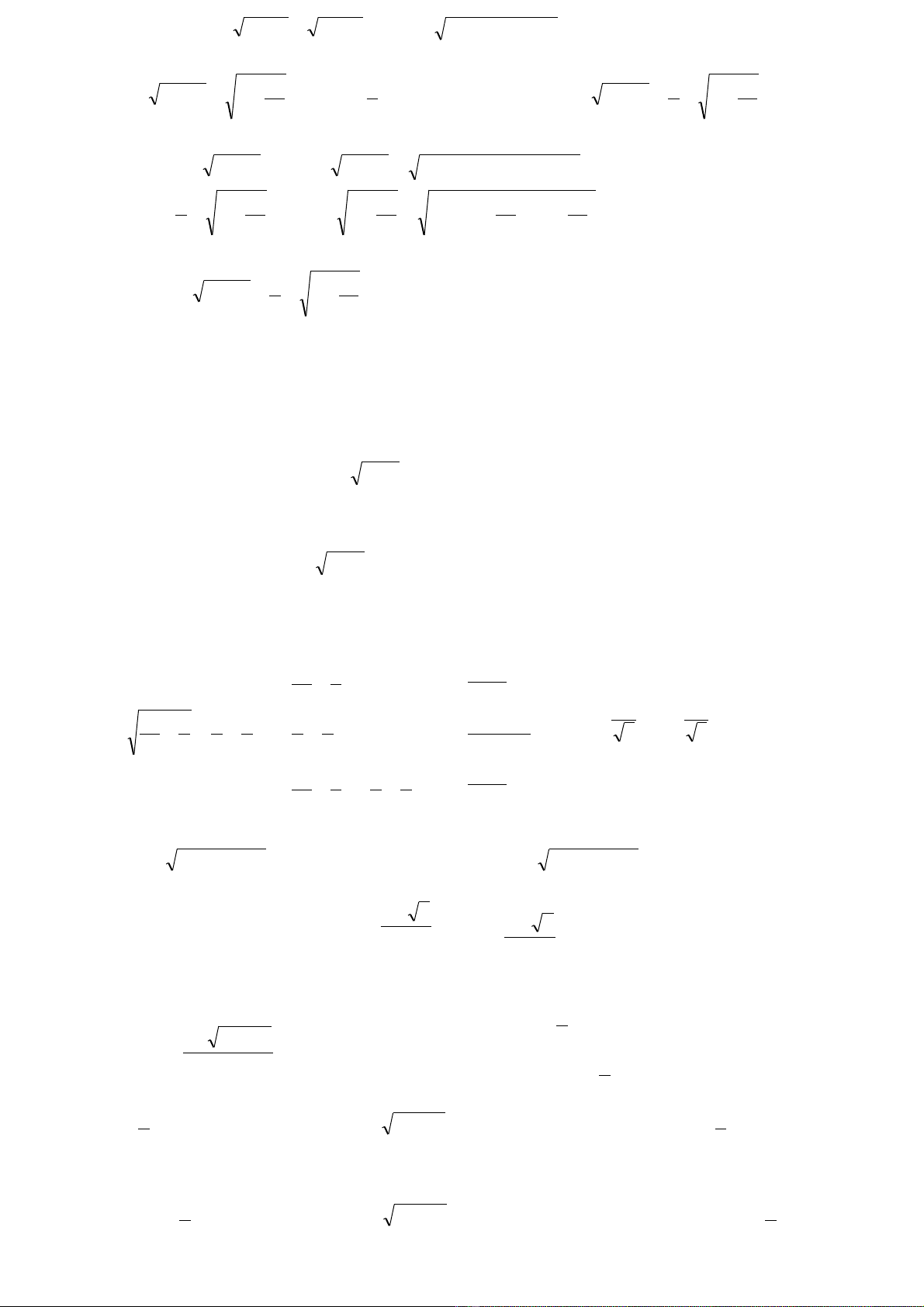
Xét v trái ta có ế
22)21)(21(22)2121( 2+≤+−+=++− xxxx
suy ra v trái ≤ 2 d u b ng x yế ấ ằ ẩ
ra khi x = 0 v y x = 0 là nghi m c a ph ng trình ậ ệ ủ ươ
Bài4:gpt:
)
1
(4
1
22 2
2
x
x
x
x+−=−+−
t ng đ ng v i ươ ươ ớ
4
1
2
1
22
2=−++−+ xx
xx
Áp d ng b t đ ng th c Bu nhi a c p ski ta có ụ ấ ẳ ứ ố
C ng ộ
=−++≤−+=−+
=−++≤−+=−+
2)
1
2(
1
)(11(
1
2.1.1
1
2
1
2)2()(11(2.1.12
22
22
22
222222
xxx
x
xx
xxxxxx
---------------------------------------------------------------------------
Ta có
4
1
2
1
22
2≤−++−+ xx
xx
d u b ng x y ra khi x=1 là nghi m c a ph ng trìnhấ ằ ẩ ệ ủ ươ
PH N 2 :B t ph ng trình có ch a cănẦ ấ ươ ứ
I)Ph ng pháp bi n đ i t ng đ ngươ ế ổ ươ ươ :
1) Ki n th c c b nế ứ ơ ả : 1)
≤≤
≥
⇔≤ )()(0
0)(
)()(
2
xgxf
xg
xgxf
2)
≥
≥
≥
<
⇔≥
)()(
0)(
0)(
0)(
)()(
2xgxf
xg
xf
xg
xgxf
2) Bài t p áp d ngậ ụ :
Bài1:
≤<
≠
≤≤−
≤<
⇔
≤
−
≤
−
≤
−
⇔
−≤−
≥−
≥−
⇔−≤−
20
0
3
4
3
4
40
0
2
0
4
163
0
2
4
2
12
4
34
0
2
12
0
4
34
2
12
4
34
2
2
2
2
2
2
x
x
x
x
x
x
x
x
x
x
xx
x
x
xx
V y t p nghi m c a b t ph ng trình là ậ ậ ệ ủ ấ ươ
(
]
2,0
Bài2: gbpt
02162 2≥+−+− xxx
t ng đ ng v i ươ ươ ớ
2162 2−≥+− xxx
t ng đ ng v iươ ươ ớ
[
)
+ ∞∪
−
∞−⇔
≥
−
≤
⇔
−≥+−
≥−
≥+−
<−
,3
2
73
,
3
2
73
)2(162
02
0162
02
22
2
x
x
xxx
x
xx
x
Bài3: gbpt:
0
411 2<
−−
x
x
đi u ki n ề ệ
≤<
<≤−
⇔
≥−
≠
2
1
0
0
2
1
041
0
2
x
x
x
x
1) V i -ớ
0
2
1<≤ x
bpt t ng đ ng ươ ươ
⇔
−<−
>−
⇔−<− 22
2
)31(41
031
3141 xx
x
xx
-
0
2
1<≤ x
2) V i 0<xớ
2
1
≤
bpt t ng đ ng ươ ươ
⇔
≥−
−>−
≥−
<−
⇔−>−
031
)31(41
041
031
3141 22
2
2
x
xx
x
x
xx
0<x
2
1
≤


























