Chuyên đ I: ng D ng Đ o Hàm Trong Các Bài Toán Đ i Sề Ứ ụ ạ ạ ố
I.Các vài toán liên quan đ n nghi m c a pt-bptế ệ ủ :
Đ nh lí 1ị: S nghi m c a pt f(x)=g(x) chính là s giao đi m c a hai đ th y=f(x) vàố ệ ủ ố ể ủ ồ ị
y=g(x)
Đ nh lí 2:ị N u hàm s y=f(x) lt trên D và ế ố
min ( )
x D
m f x
=
,
ax ( )
x D
M M f x
=
thì pt: f(x)=k có
nghi m khi và ch khi ệ ỉ
m k M
Đ nh lí 3:ị B t ph ng trình ấ ươ
( ) ( )f x g x
nghi m đúng m i x thu c D khi và ch khi ệ ọ ộ ỉ
( ) ( )
x D x D
Min f x Max g x
� �
Các ví dụ:
Bài 1:Tìm m đ pt sau có nghi m: ể ệ
2 2
1 1x x x x m+ + − − + =
(HSG Ngh an 2005ệ)
L i gi i: Xét hàm s ờ ả ố
2 2
( ) 1 1f x x x x x
= + + − − +
có t p xác đ nh là D=Rậ ị
( )
( )
+ −
= − =� �
+ + − +
+ − + = − + +
� � � �
+ + = − + + =� �
� � � �
� � � �
2 2
2 2
2 2
2 2
2 1 2 1
'( ) ' 0
2 1 2 1
(2 1) 1 2 1 1 (1)
1 1 3 1 1 3
[( - ) ] [( ) ] 0 thay vaøo (1)ta thaáy khoâng
2 2 4 2 2 4
thoûa maõn. Vaäy f'(x)=0 voâ nghieäm, maø f'(0)=1>0, do
x x
f x f x
x x x x
x x x x x x
x x x x x
−
∀
= = −
+ + + − +
< <�
2 2
x +
x +
ñoù f'(x)>0 x
2
Maët khaùc: Lim ( ) =Lim 1; Lim ( ) 1
1 1
Vaäy pt ñaõ cho coù nghieäm -1 1
x
R
x
f x f x
x x x x
m
Bài 2:Tìm t t c các giá tr c a a đ pt: ấ ả ị ủ ể
có đúng m t nghi mộ ệ
0; 2
x
π
� �
� �
� �
(Đ thi HSG t nh H i D ng L p 12 năm 2005ề ỉ ả ươ ớ )
Gi iả: Ta th y đ pt có nghi m thì ấ ể ệ
0a
( )
π
π π
−� �
= =� � �
� �
� �
� �
� �
� �
−� � � �
= < ∀ ��
� � � �
� � � �
2
2 2
2 2
sin
cos 1 sin
2
Khi ñoù pt =a -2 . Xeùt haøm soá ( ) vôùi t 0; 4
2
cos -
.cos sin
ta coù '( ) = 0 vôùi t 0; ( ) ngb treân 0;
4 4
t
x
x t
a f t t
xx
t t tgt
t t t
f t f t
t
π π
π π π
π
π π
= < < < < ∀� � �
� �
� �
� �
< − < − < < −� � �
2
2 2
0
2 2
sin
2 2 2 2 8 2
Maø f( )= vaø ( ) 1 ( ) 1 1 (0; )
4 2
2
8 1 4
Vaäy pt ñaõ cho coù ñuùng 1 nghieäm (0; ) 2 1
2 2
t
x
Lim f t f t x
x
x a a
Bài 3: Cho ph ng trìnhươ
+ − − − + + =
6 5 4 3 2
3 6 ax 6 3 1 0x x x x x
. Tìm t t c các giáấ ả
tr c a tham s a, đ ph ng trình có đúng 2 nghi m phân bi t.ị ủ ố ể ươ ệ ệ (HSG Nam Đ nhị
2004)
Gi i:ả Vì
0x=
không ph i là nghi m pt. Chia hai v pt cho xả ệ ế 3 ta đ cượ
+ + + − + − +
− + − − = + − = +�
−+ = ∆�۳
=
3 2
3 2
2 2 3 2
2 2
1 1 1 1
( ) 3( ) 6( ) a=0 (1). Ñaët t= ta thu ñöôïc pt
( 3) 3( 2) 6 3 9 6 (1')
Töø caùch ñaët t ta coù: 1 0 (2)pt naøy coù = - 4 0 2. Töø ñaây ta coù
*Neáu 2 thì pt
x x x x
x x
x x
t t t t a t t t a
x tx t t
t
>
۱
ñaõ cho coù moät nghieäm
*Neáu 2 thì vôùi moãi giaù trò cuûa cho töông öùng hai giaù trò cuûa x
Neân pt (1) coù ñuùng hai nghieäm phaân bieät pt(1') coù ñuùng hai nghieäm t= 2
hoaëc (1') coù ñuùng
t t
>
= +
= +
>
= + − > = + − = −
3 2 2
1nghieäm thoûa maõn 2
2 6
1: Neáu (1') coù ñuùng hai nghieäm t= 2 voâ nghieäm
22 6
2:(1') coù ñuùng moät nghieäm 2
Xeùt haøm soá ( ) 3 9 vôùi 2, ta coù '( ) 3 6 9 3( 1
t t
a
TH a
TH t
f t t t t t f t t t t +)( 3)t
Ta có b ng bi n thiên: ả ế
D a vào b ng bt ta th y pt(1’) có đúng m t nghi m ự ả ấ ộ ệ
>2t
khi và ch khiỉ
< + < − < <�2 6 22 4 16a a
f(t)
f’(t)
x-2 21-3
00+-
2
22
27
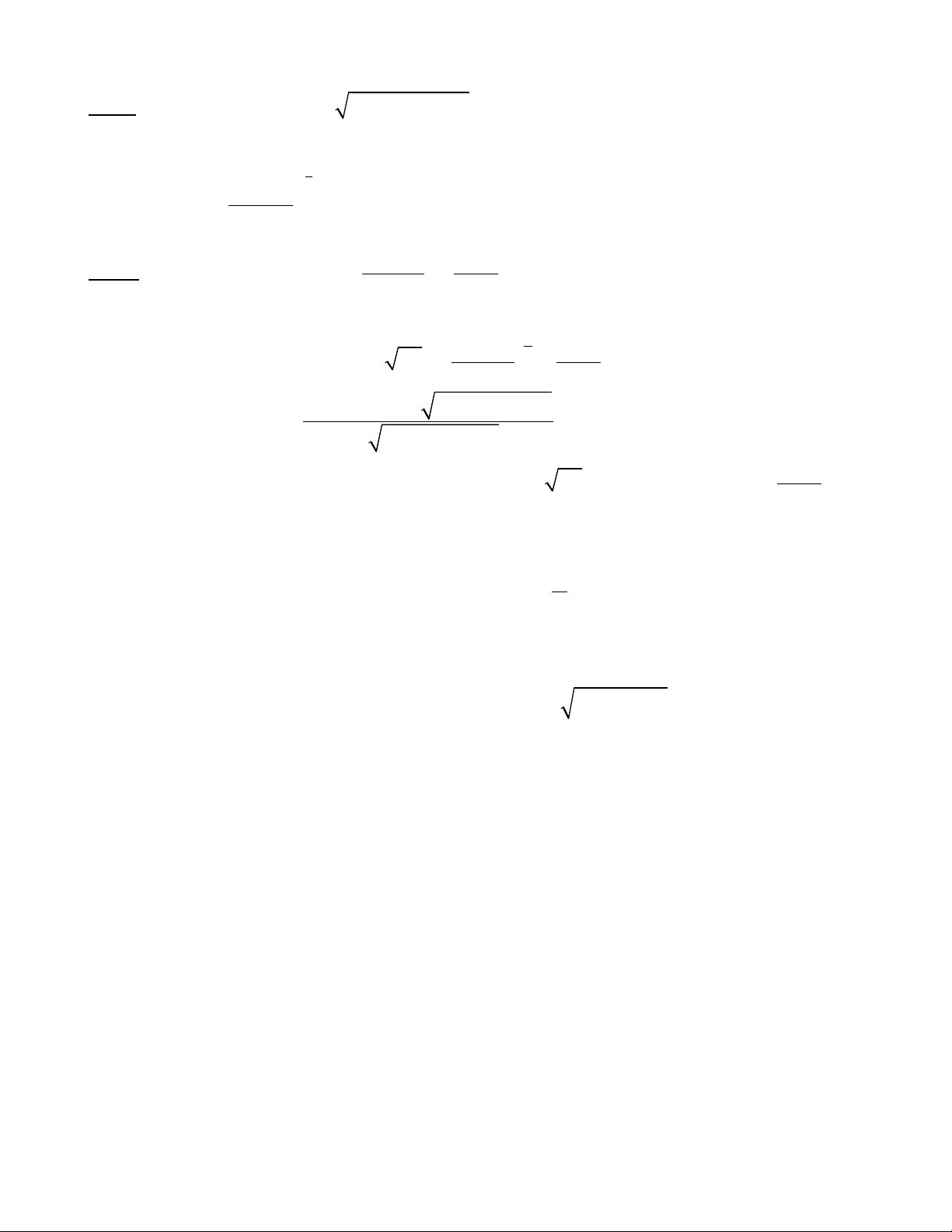
Bài 4:Cho hàm s ố
= − + + +( )( )y x x a x b
v i a,b là hai s th c d ng khác nhau choớ ố ự ươ
tr c.Cmr v i m i s th c ướ ớ ỗ ố ự
( )
0;1s
đ u t n t i duy nh t s th cế ồ ạ ấ ố ự
α α
� �
+
> = � �
� �
1
0: ( ) 2
s s s
a b
f
( HSG QG b ng A năm 2006)ả
Gi i:ả Tr c h t ta cos BĐT : ướ ế
+ +
( )
2 2
s s s
a b a b
(1) ta có th cm (1) b ng hàm sể ằ ố
ho c b ng BĐT Bécnuliặ ằ
Áp d ng BĐT Côsi và (1) ta có : ụ
1
( )
2 2
s s
s
a b a b
ab + +
< <
(*) (do
a b
)
M t khác ta có: ặ
2 2 ( )( )
'( ) 2 ( )( )
x a b x a x b
f x x a x b
+ + − + +
=+ +
ta d dàng cm đ c f’(x) >0 m iễ ượ ọ
x>0 suy ra f(x) đ ng bi n v i x>0 nên ồ ế ớ
0
( ) ( ) ( ) 2
x
x
a b
Lim f x ab f x Lim f x
+ +
+
= =
(**)
Vì f(x) liên t c khi x>0 nên t (*) và (**) ta có đi u ph i cmụ ừ ề ả
Bài t p:ậ
1. Tìm m đ pt sau có nghi m duy nh t thu c ể ệ ấ ộ
π
[0; ]
4
− + − + − − − =
3 2
(4 6 )sin 3(2 1)sin 2( 2)sin cos (4 3)cos 0m x m x m x x m x
2.Tìm m đ s nghi m c a pt: ể ố ệ ủ
2 2 4 2
15 2(6 1) 3 2 0x m x m m− + − + =
không nhi u h nề ơ
s nghi m c a pt: ố ệ ủ
2 3 6 8
(3 1) 12 2 6 (3 9) 2 0,25
x m m
m x x
− + + = − −
(HSG Ngh anệ
1998)
3. Tìm t t c các giá tr a đ bpt: ấ ả ị ể
2
ln(1 ) x x ax+ −
nghi m đúng ệ
0x∀
4. a)Cmr n u a >0 là s sao cho bpt: ế ố
1
x
a x +
đúng v i m i ớ ọ
0x
thì
a e
b) Tìm t t c các giá tr c a a đ : ấ ả ị ủ ể
1
x
a x x + ∀
(HSG 12 Nam Đ nh 2006)ị
II.Gi i pt b ng ph ng pháp hàm s :ả ằ ươ ố
Đ nh lí 1ị:N u hàm s y=f(x) luôn đb (ho c luôn ngb) thì s nghi m c a pt : f(x)=kế ố ặ ố ệ ủ
Không nhi u h n m t và f(x)=f(y) khi và ch khi x=yề ơ ộ ỉ
Đ nh lí 2ị: N u hàm s y=f(x) luôn đb (ho c luôn ngb) và hàm s y=g(x) luôn ngbế ố ặ ố
(ho c luôn đb) trên D thì s nghi m trên D c a pt: f(x)=g(x) không nhi u h n m tặ ố ệ ủ ề ơ ộ
Đ nh lí 3ị:Cho hàm s y=f(x) có đ o hàm đ n c p n và pt ố ạ ế ấ
( ) ( ) 0
k
f x =
có m nghi m,ệ
khi đó pt
( 1) ( ) 0
k
f x
−=
có nhi u nh t là m+1 nghi mề ấ ệ
Các ví d :ụ
Bài 1:Gi i pt:ả
2 2
3 (2 9 3) (4 2)( 1 1) 0x x x x x+ + + + + + + =
(Olympic 30-4 ĐBSCL 2000)
Gi i:ả Ta th y pt ch có nghi m trong ấ ỉ ệ
1
( ;0)
2
−
( )
2 2
2 2
3 (2 ( 3 ) 3) (2 1)(2 (2 1) 3)
(2 3) (2 3) (1)
pt x x x x
u u v v
− + − + = + + + +�
+ + = + +�
V i u=-3x, v=2x+1; u,v>0. Xét hàm s ớ ố
4 2
( ) 2 3f t t t t
= + +
v i t>0ớ
Ta có
3
4 2
2 3
'( ) 2 0 0 ( ) ( )
3
t t
f t t f u f v u v
t t
+
= + > ∀ > = =� �
+
(1)
u=v
-3x=2x+1
1
5
x= −�
là nghi m duy nh t c a ptệ ấ ủ
Bài 2: Gi i pt: ả
π π
� �
+ � �
� �
2osx=2 vôùi - ;
2 2
tg x
e c x
(HSG L p 12 Nam Đ nh 2006)ớ ị
Gi i:ả Xét hàm s : ố
π π
� �
= + � �
� �
2
( ) osx vôùi - ;
2 2
tg x
f x e c x
, ta có
� �
−
� �
= − = � �
� �
2
2tg 3
2 3
1 2e os
'( ) 2 . sin sin
cos os
x
tg x c x
f x tgx e x x
x c x
Vì
> >
23
2 2 os 0
tg x
e c x
Nên d u c a f’(x) chính là d u c a sinx. T đây ta có ấ ủ ấ ủ ừ
=( ) (0) 2f x f
V y pt đã cho có nghi m duy nh t x=0ậ ệ ấ
Bài 3: Gi i pt: ả
+ = +2003 2005 4006 2
x x
x
(HSG Ngh an 2005)ệ
Gi i: ảXét hàm s : ố
= + − −( ) 2003 2005 4006 2
x x
f x x
Ta có:
=+−'( ) 2003 ln2003 2005 ln2005 4006
x x
f x
= + > ∀ =�
� �
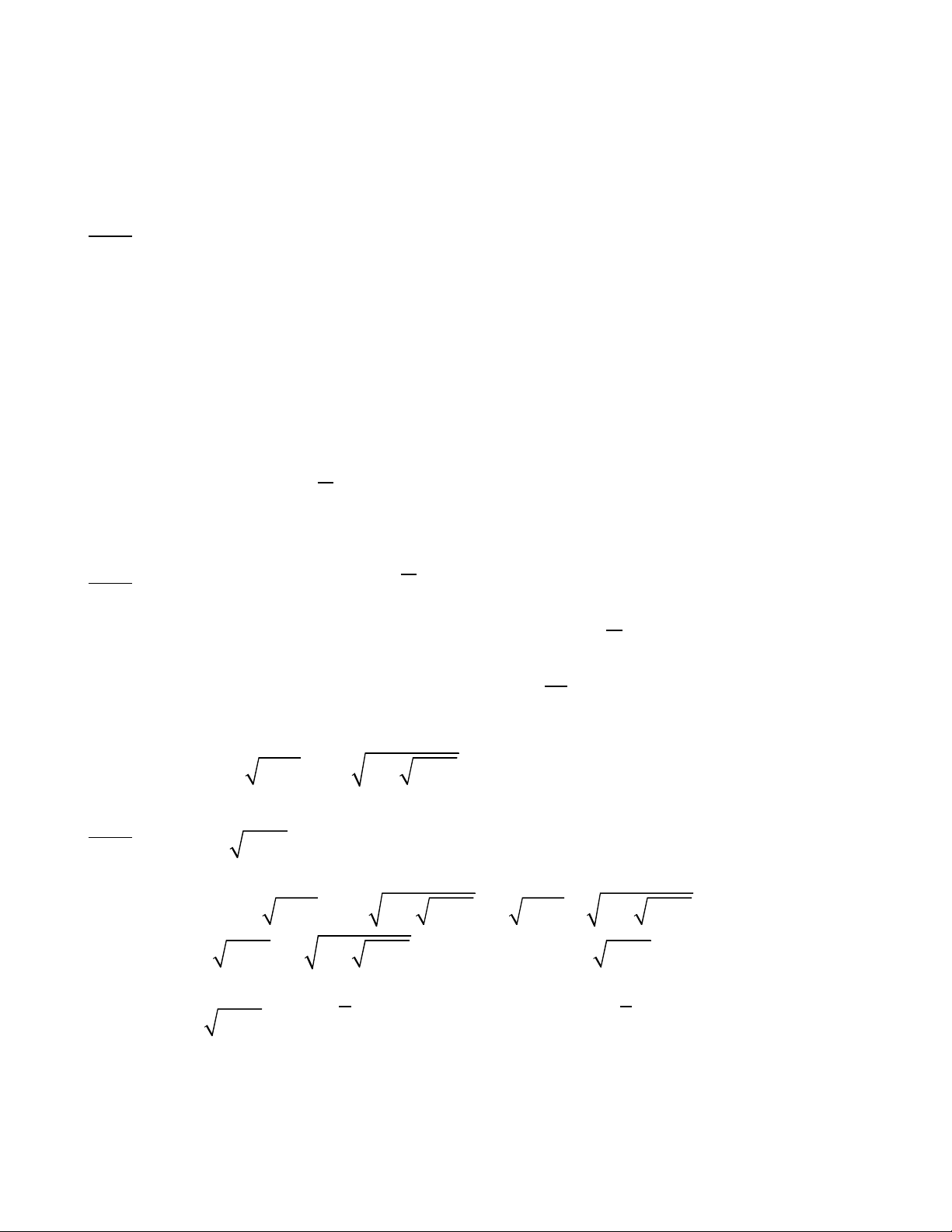
2 2
''( ) 2003 ln 2003 2005 ln 2005 0 "( ) 0 voâ nghieäm
f'(x)=0 coù nhieàu nhaát laø moät nghieäm f(x)=0 coù nhieàu nhaát laø hai nghieäm
x x
f x x f x
Mà ta th y f(1)=f(0)=0 nên pt đã cho có hai nghi m x=0 và x=1ấ ệ
Bài 4: Gi i pt: ả
= + + +
3
3 1 log (1 2 )
xx x
(TH&TT)
Gi iả: Đk: x>-1/2
+ = + + + + = + + +� �
3 3 3
3 1 2 log (1 2 ) 3 log 3 1 2 log (1 2 )
x x x
pt x x x x x
(1)
Xét hàm s : ố
= + 3
( ) logf t t t
ta có f(t) là hàm đ ng bi n nênồ ế
= + = + − − =� � �(1) (3 ) (1 2 ) 3 2 1 3 2 1 0 (2)
x x x
f f x x x
Xét hàm s : ố
= − − = − = >� �
2
( ) 3 2 1 '( ) 3 ln3 2 "( ) 3 ln 3 0
x x x
f x x f x f x
=� ( ) 0f x
có nhi u nh t là hai nghi m, mà f(0)=f(1)=0 nên pt đã cho có hai nghi mề ấ ệ ệ
x=0 và x=1
Bài 5: Gi i h pt: ả ệ
π
>
sinx-siny=3x-3y (1)
x+y= (2)
5
, 0 (3)x y
Gi iả: T (2) và (3) ta có : ừ
π
, (0; )
5
x y
(1) sinx-3x=siny-3y
. Xét hàm s f(t)=sint-3t v i ố ớ
π
(0; )
5
t
ta có f(t) là hàm ngh chị
bi n nên f(x)=f(y)ế
x=y thay vào (2) ta có
π
= = 10
x y
là nghi m c a hệ ủ ệ
Bài 6: Gi i h : ả ệ
− = −
+ − = − +
(1)
1 1 8 (2)
tgx tgy y x
y x y
(30-4 MOĐBSCL 2005)
Gi iả: Đk:
−
+
1
8
y
x y
(*)
(1)
tgx x tgy y+ = +�
x y=�
(do hàm s ố
( ) f t tgt t= +
là hàm đ ng bi n)ồ ế
Thay vào (2) ta có:
+ − = − + + = − + +�1 1 8 1 8 1y y y y y y
+ = − + + − + + + = − +� �
� �
� �
− = + =� � � �
� �
� �
− + = + − − =
� �
2 2
1 8 2 8 1 8 4 4 8
8 8
3 3
3 8 4 8 8
9 48 64 16 128 9 64 64 0
y y y y y y y y
y y
y y y
y y y y y
V y ậ
8 x y= =
là nghi m duy nh t c a h đã cho ệ ấ ủ ệ