Ấ
ẤẤ
Ấ
Ấ
ẤẤ
Ấ
Ẳ
ẲẲ
Ẳ
Ẳ
ẲẲ
Ẳ
!
!
"
" !
!
#
#
$
$%
%
&'
&'
(
($
$)
)
*
*
+
+,
,
%
%
-
-$
$)
)
*
*
.
.'
'
/
/
0
01
1
2
2
+
+'
'
/
/
3
34
45
5
%
%
6
67
7
8
8
9
9
:
:;
;
<
<
=
=
>
>
5
5
;
;
?
?!
!@
@
8
8
A
A1
1
:
:)
)
B
B!
!C
C2
2 4
45
5
C
C
D
D
=
=
4,
4,
3
32
2
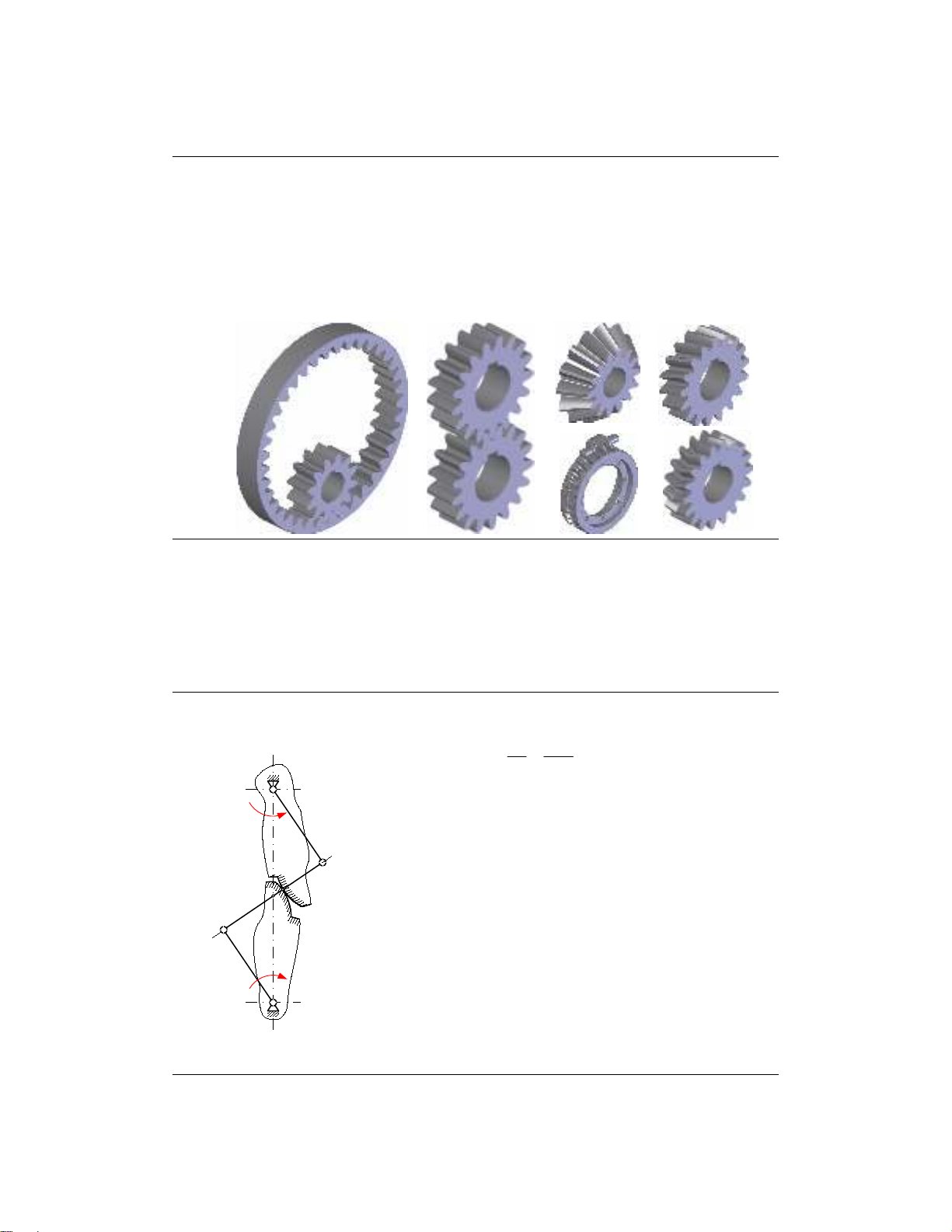
E
E !
!
#
#
$
$%
%
&'
&'
(
($
$)
)
*
*
+
+,
,
%
%
F
F
)
)
G
G
=
=
>
>
.
.'
'
/
/
0
01
1
2
2
H
H
'
'
/
/
0
01
1
2
2 4I
4I
F
F
J
J
6
6%
%
0
01
1
2
2.
.0
01
1
2
2
>
>
0
01
1
2
2 I
I
F
F!
!C
C2
2 4
45
5
.
.
F
F
1
1
0
0@
@
G
G2
2 K
K 0
01
1
2
2.
.0
01
1
2
2
H
H
0
01
1
2
2 K
K
=
=L
L
-
-,
,
%
%
'
'
/
/
0
01
1
2
2 2
2 4
45
5
+
+
2
2 4
45
5
M
M !
!
#
#
$
$%
%
&'
&'
((
(($
$)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
-
-
?
?!
!@
@
8
8
-
-$
$)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
.
.$
$9
9
?
?!
!@
@
8
8
@
@:
:)
)
:&
:&B
B
1
1
D
D
P
P
;
;
Q
Q
0K
0K 6
6%
%
O
O
I
I
R
R
:&
:&B
B
@
@
,
,
%
%
;
;
:
:9
9
@
@:
:)
)
-
-LS
LS 2
2
F
F
+
+,
, 2
2 4
45
5
F
F
F
F
S
S S
S
+
+2
2 4I
4I &
&T
T
K
K
U
U
+
+S
S 2
2
1
1
0
01
1
4
4G
G
:&
:&T
T
4N
4N
V
V
F
F
Q
Q
0
01
1
2
2
;
;
W
W
%
%
X
X
D
D
4
4
S
S 2
2
;
;
W
W
%
%
X
X
D
D
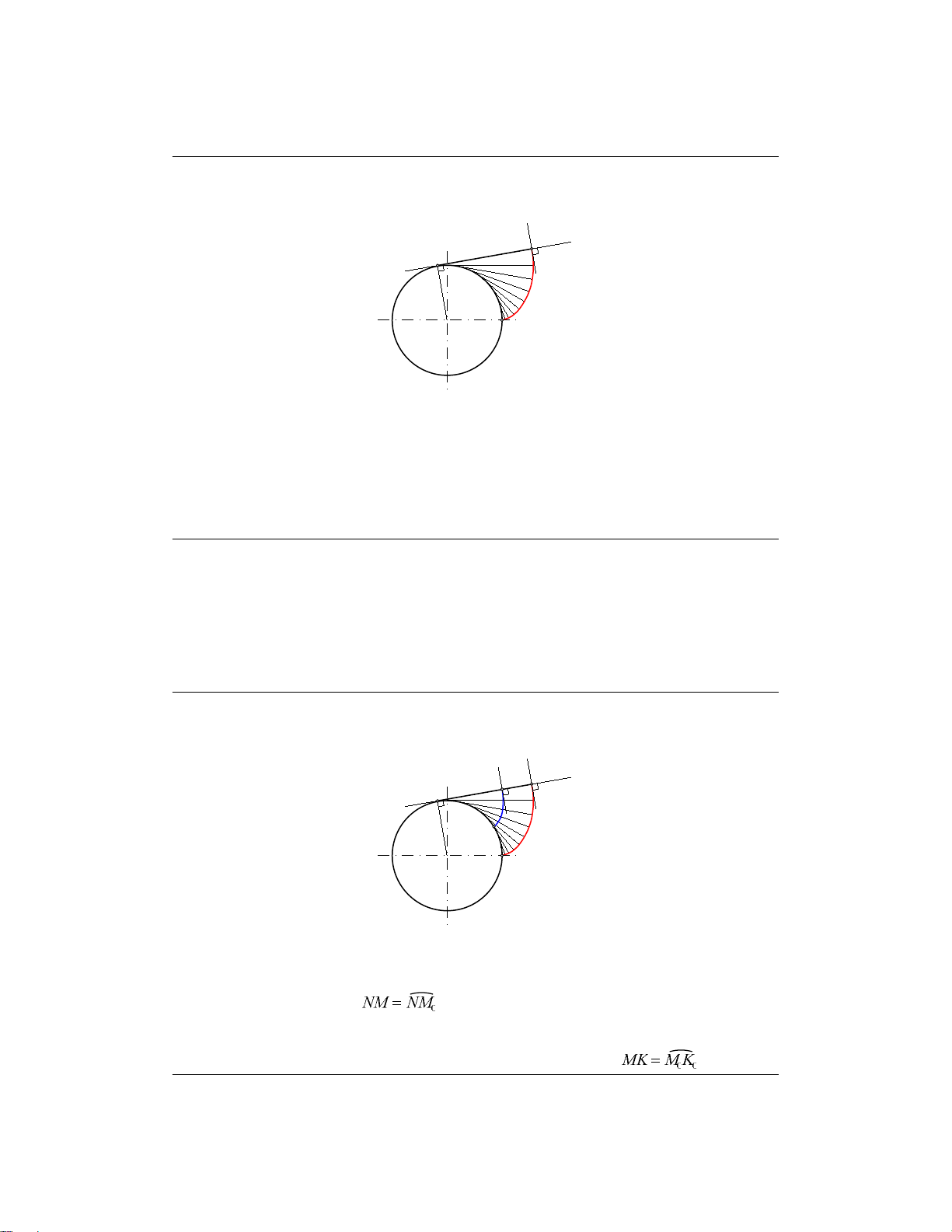
Y
Y !
!
#
#"
"
Z
Z
:&
:&B
B
,
, 4
4
7
7
T
T
5
5
:
:)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
(
($&
$&B
B
,
, 4
4
+
+
1
1
G
G
/
/
-
-$&
$&B
B
,
, 4
4.
.
LS
LS S
S W
W
X
X
U
U
+
+S
S '
' !
![
[
:&
:&B
B
H
H
2
2 4I
4I &
&T
T
K
K S
S S
S W
W
X
X0
0/
/
4
4\
\:
:9
9
+
+
;
;
!
!]
]
%
%
K
K
;
;
:&
:&B
B
U
U
+
+:&
:&B
B
,
, 4
4
^
^ !
!
#
#"
"
Z
Z
:&
:&B
B
,
, 4
4
7
7
T
T
5
5
:
:)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
(
($&
$&B
B
,
, 4
4
+
+
1
1
G
G
/
/
-
-
G
G
/
/
P
P
:&
:&B
B
,
, 4
4
$&
$&B
B
,
, 4
4 4I
4I
3
3:
:9
9
+
+
_
_
S
S '
' !
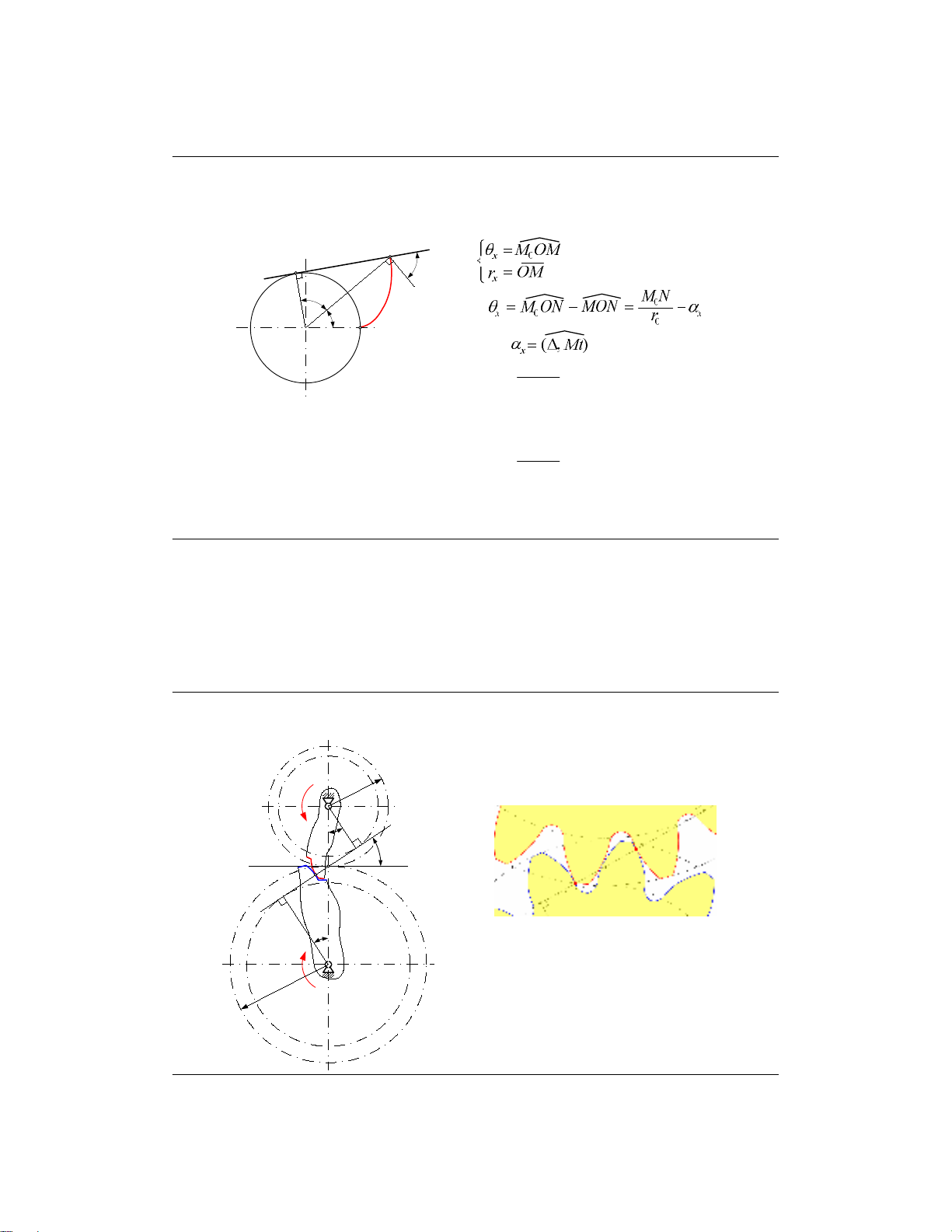
b
b !
!
#
#"
"
Z
Z
:&
:&B
B
,
, 4
4
7
7
T
T
5
5
:
:)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
((
((&'
&'
J
J
:&
:&B
B
,
, 4
4
-
-
U
U
V
V
:
:;
;
C
C
5
5
+
+
@
@
:
:9
9
;
;
:&
:&T
T
A
A1
1
:
:)
)
0
0[
[
.
.
3
3
1
1
C
C
&'
&'
J
J
:&
:&B
B
,
, 4
4
:&
:&T
T
U
U
+
+
+
+
+
+
,
, 4
4
c
c !
!
#
#"
"
Z
Z
:&
:&B
B
,
, 4
4
7
7
T
T
5
5
:
:)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
(((
((($&
$&B
B
,
, 4
4
7
7
T
T
5
5
:
:)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
-
-$
$)
)
N
N '
' 0
0O
O
8
82
2 4
45
5
.
.
$
$9
9
?
?!
!@
@
8
8
@
@:
:)
)
:&
:&B
B
1
1
D
D
P
P
;
;
Q
Q
0K
0K 6
6%
%
O
O
I
I
R
R
:&
:&B
B
@
@
,
,
%
%
;
;
:
:9
9
@
@:
:)
)
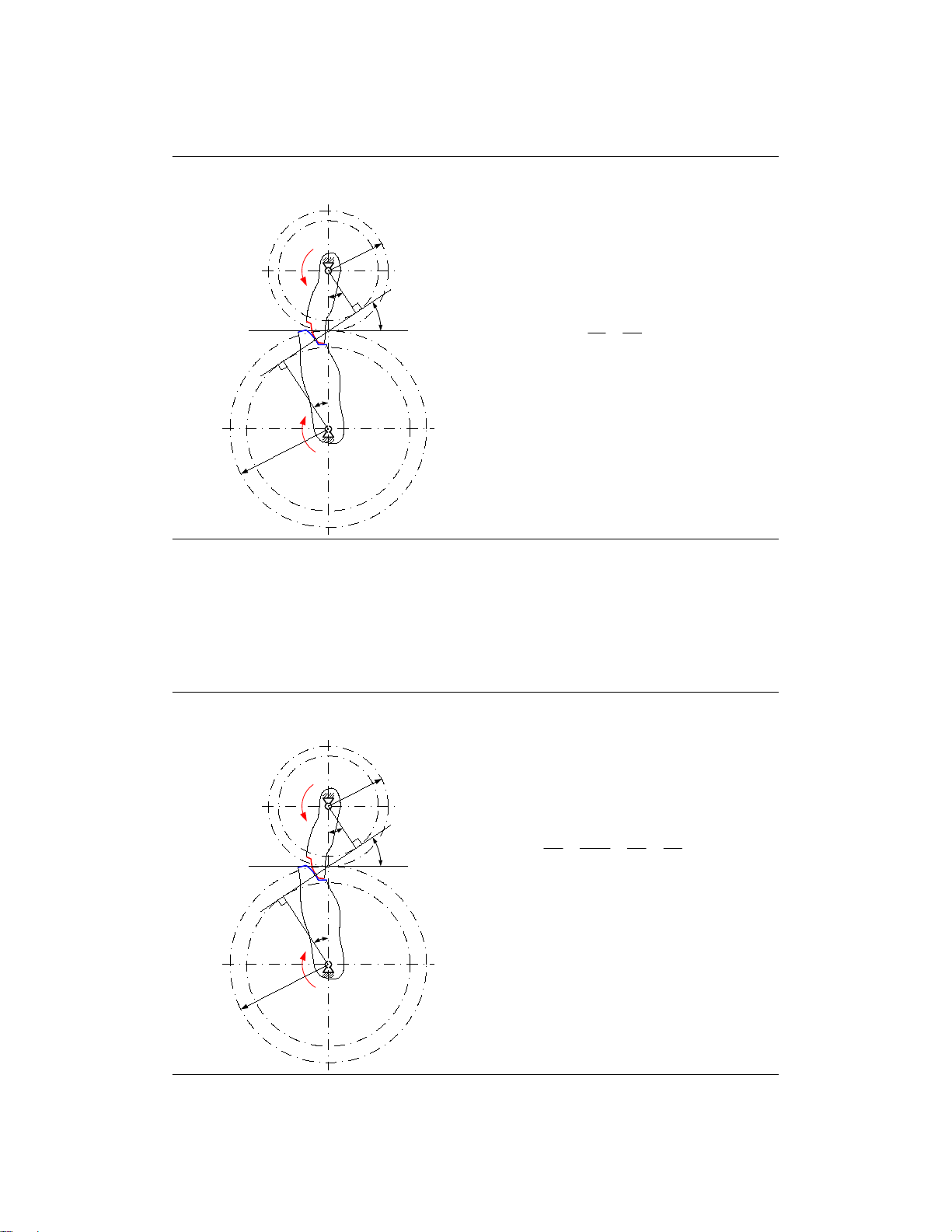
d
d !
!
#
#E
E$
$Q
Q
:
:9
9
P
P
0
01
1
2
2 ,
, 4
4
(
($&
$&B
B
2
2 4
45
5
3
3
2
2 4
45
5
-
-$&
$&B
B
2
2 4
45
5
N
N
D
D
-
-
3
3
2
2 4
45
5
.
.0
01
1
4
4G
G
S
S '
' !
![
[0
01
1
2
2
+
+"
"
.
.0
01
1
4
4G
G
S
S 2
2 0
01
1
2
2
+
+"
"
-
-
3
3
2
2 4
4ớ
ớ
:&
:&ờ
ờ
2
2 4
4ớ
ớ
S
S 2
2
ụ
ụ
ộ
ộ
+
+
4
4ả
ả
1
1
ụ
ụ
ứ
ứ
ụ
ụ
ộ
ộ
+
+
4
4ả
ả
1
1
&'
&' :
:ố
ố
ữ
ữ
0
01
1
2
2
!
!
#
#E
E$
$Q
Q
:
:9
9
P
P
0
01
1
2
2 ,
, 4
4
((
((a
aO
O2
2 6
6)
)
,
,
-
-a
a 4
4O
O
1
1
>
>
:
:e
e
1
1
0
01
1
4
4G
G
S
S 2
2
:
:e
e
&
&
?
?!
!@
@
8
8
f
f
@
@
:
:)
)
-
-$,
$,
+
+
;
;
:
:Q
Q
:
:9
9
+
+
+
+
;
;
&
& :
:9
9
P
P
0
01
1
2
2 ,
, 4
4
J
J4
4
R
R
1
1
D
D
4
4O
O
1
1
>
>
4I
4I :
:O
O
0
0O
O
?
?!
!@
@
8
8
f
f
:
:O
O
0
0O
O
![Chương trình khung trình độ cao đẳng nghề Cắt gọt kim loại - Trường CĐN KTCN Dung Quất [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2021/20210417/tradaviahe20/135x160/1301618651048.jpg)
![Tổng hợp 58 câu hỏi về đồ án Chi tiết máy [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2020/20201015/daohachi0512/135x160/9011602770055.jpg)
![Bài tập tối ưu trong gia công cắt gọt [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251129/dinhd8055/135x160/26351764558606.jpg)
