CH NG II – HÀM S B C NH TƯƠ Ố Ậ Ấ
BÀI 1: NH C L I VÀ B SUNG CÁC KHÁI NI M V HÀM SẮ Ạ Ổ Ệ Ề Ố
1) a) f(-2) = 2/3(-2) = -4/3; f(-1) = -2/3; f(0) = 0; f(1/2) = 1/3; f(1) = 2/3; f(2) = 4/3; f(3) = 2.
b) g(-2) =5/3; g(-1) =7/3; g(0) = 3; g(1/2) = 10/3; g(1) = 11/3; g(2) = 13/3; g(3) = 5.
c) Khi x l y cùng m t giá tr thì giá tr c a g(x) l n h n giá tr c a f(x) là 3 đn v .ấ ộ ị ị ủ ớ ơ ị ủ ơ ị
2)V i y = -1/2x + 3, ta cóớ :f(-2,5) = -1/2(-2,5) + 3 = (2,5 + 6)/2 = 4,25;
T ng t : f(-2) = 4; f(-1,5) = 3,75 ; f(-1) = 3,5 ươ ự ; f(-0,5) = 3,25; f(0) = 3; f(0,5) = 2,75; f(1) = 2,5 ; f(1,5) = 2,25
; f(2) = 2 ; f(2,5) = 1,75.
3)
a) Đ th c ahàm s y = 2x là đng th ng đi qua O và đi m A(1; 2).ồ ị ủ ố ườ ẳ ể
Đ th c a hàm s y = -2x là đng th ng đi qua O và đi m B(1; -2).ồ ị ủ ố ườ ẳ ể
b) Hàm s y = 2x đng bi n vì khi x tăng lên thì y t ng ng tăng lên.ố ồ ế ươ ứ
Hàm s y = -2x ngh ch bi n vì khi x tăng lên thì y t ng ng gi m đi.ố ị ế ươ ứ ả
4)Ta bi t r ng đ th hàm s y = √3 xế ằ ồ ị ố là m t đng th ng đi qua g c t a đ. H n n a, khi x = 1 thì y = √3. ộ ườ ẳ ố ọ ộ ơ ữ
Do đó đi m A(1; √3) thu c đ th . Vì th đ v đ th này, ta ph i xác đnh đi m A trên m t ph ng t a đ. ể ộ ồ ị ế ể ẽ ồ ị ả ị ể ặ ẳ ọ ộ
Mu n v y ta ph i xác đnh đi m trênố ậ ả ị ể tr c tung bi u di n s √3. Ta có:ụ ể ễ ố
x -2,5 -2 -1,5 -1 -0,5 0 0,5 1 1,5 2 2,5
y=-1/2x + 3 4,25 4 3,75 3,5 3,25 3 2,75 2,5 2,25 2 1,75
y= 2x -1 0 1 2
y =-2x -2 0 2 4
y= -2x 2 0 -2 -4
Hình v trong SGK th hi n OC = OB = √2 và theo đnh lí Py-ta-goẽ ể ệ ị
Dùng compa ta xác đnh đc đi m bi u di n s √3. trênị ượ ể ể ễ ố
Oy. T đó xác đnh đc đi m A.ừ ị ượ ể
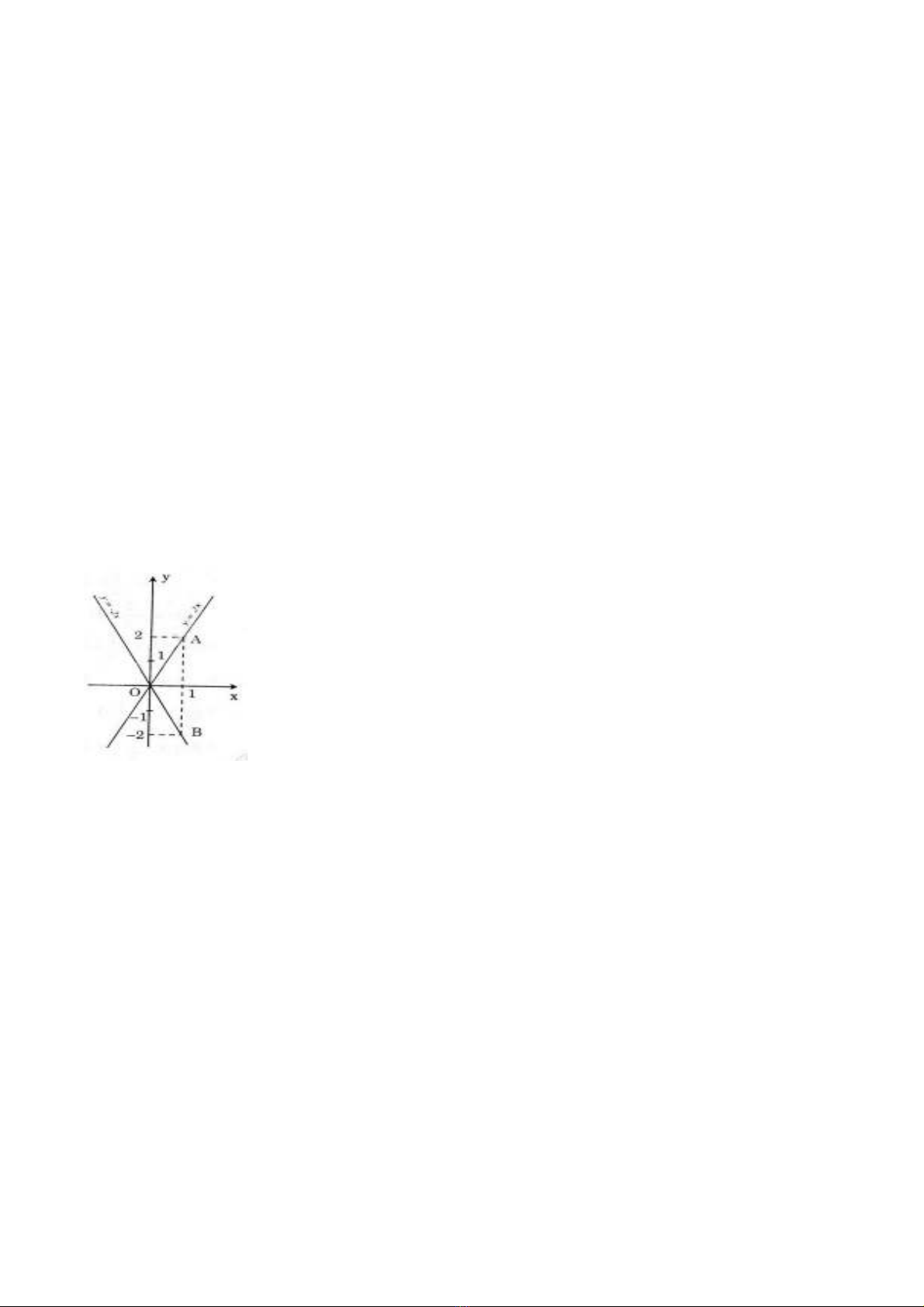
5)a)
b) A(2; 4), B(4; 4).
.
6)a) Tính cá c giá tr c aị ủ y ta đc:ượ
x -2,5 -2,25 -1,5 -1 0 1 1,5 2,25 2,5
y= 0,5x -1,25 -1,125 -0,75 -0,5 0 0,5 0,75 1,125 1,25
y = 0,5x + 2 0,75 0,875 1,25 1,5 2 2,5 2,75 3,125 3,25
Khi x l y cùng m t giá tr thì giá tr c a hàm s y = 0,5x + 2 l n h n giá tr c a hàm s y = 0,5x là 2 đn v .ấ ộ ị ị ủ ố ớ ơ ị ủ ố ơ ị
7) ng v i giá tr x1 thì hàm s nh n giá tr f(x1) = 3×1Ứ ớ ị ố ậ ị
ng v i giá tr x2 thì hàm s nh n giá tr f(x2) = 3×2Ứ ớ ị ố ậ ị
Xét hi u f(x1) – f(x2) = 3×1 – 3×2 ệf3(x1 – x2) (1)
Theo gi thi t ả ế x1 < x2 nên x1 – x2 < 0 (2)
Từ (1) và (2) ta suy ra: f(x1) – f(x2) < 0 ó f(x1) < f(x2)
V y x1 < x2 => ậ f(x1) < f(x2) (3)
Vì x1, x2 là hai s th c b t kì nên t (3) ta k t lu n hàm s y = 3x đng bi n trên t p s th ucj R vì (3) đúngố ự ấ ừ ế ậ ố ồ ế ậ ố ứ
v i m i giá tr b t kì cua x ớ ọ ị ấ ∈ R.
BÀI 2: Hàm s b c nh tố ậ ấ
8)a)y=1–5x là m t hàm s b c nh t v i a=-5,b=1. Đó là m t hàm s ngh ch bi n vì -5 < 0.ộ ố ậ ấ ớ ộ ố ị ế
b)y=-0,5x là m t hàm b c nh t v i a=ộ ậ ấ ớ -0,5,b = 0.Đó là m t hàm s ngh ch bi n vì -0,5 <0.ộ ố ị ế
c) y = √2(x – 1) + √3 là m t hàm s b c nh t v i a = √2, b = √3 – √2. Đó là m t hàm s đng bi n vì √2 >ộ ố ậ ấ ớ ộ ố ồ ế
0.
d) y = 2x2 + 3 không ph i là m t hàm s b c nh t vì nó không có d ng y = ax + b, v i a≠ 0.ả ộ ố ậ ấ ạ ớ
9) a) Hàm s b c nh t y = (m – 2)x + 3 đng bi n khi ố ậ ấ ồ ế m -2 > 0 ⇔ m > 2;
b) Hàm s b c nh t y = (m – 2)x + 3 ngh chố ậ ấ ị bi n khi ế m -2 < 0 ⇔ m < 2.
Chú ý khi m = 2, ta có hàm h ng y = 3.ằ
10) Khi b t m i kích th c x (cm) thì đc m t hình ch nh t có cá kích th c là 20 – x (cm) và 30 – x ớ ỗ ướ ượ ộ ữ ậ ướ
(cm). Khi đó chu vi c a hình ch nh t là y = 2(20 – x + 30 – x) hay y = 100 – 4x.ủ ữ ậ
11)
12)Thay x = 1, y =2,5 vào y = ax + 3 ta có: 2,5 = a . 1 +3. Suy ra a = 2,5 – 3 = -0,5.
Hàm s đã cho là y= -0,5x + 3.ố
13) Mu n cho m t hàm s là hàm s b c nh t thì nó ph i có d ng y = ax + b, v i a ≠ 0. Do đó:ố ộ ố ố ậ ấ ả ạ ớ a) Đi u ề
ki n là:√5-mệ ≠ 0 hay 5 – m > 0. Suy ra m < 5.
b) Đi u ki n là:m+1/m -1≠ 0 hay m + 1 ≠ 0, m – 1 ≠ 0. Suy ra m ≠ề ệ ± 1
14) a) Hàm s ngh ch bi n trên R vì 1 – √5 < 0.ố ị ế
b) Khi x = 1 + √5 thì y = -5.
c) Khi y = √5
V y x = -1/2( 3 +ậ √5)