www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
___________________________________________________________
C©u 1
1) B¹n ®äc tù gi¶i nhÐ!
2) LÊy A(0, b) lµ mét ®iÓm trªn Oy. §−êng th¼ng qua A, víi hÖ sè gãc k cã ph−¬ng tr×nh :
y = kx + b.
Ta cã
2
xx1 1
yx
x1 x1
−+
==+
−−
; 2
1
y' 1
(x 1)
=− −
Hoµnh ®é tiÕp ®iÓm cña ®−êng th¼ng y = kx + b víi ®å thÞ (C) lµ nghiÖm cña hÖ
2
1
xkxb
x1
1
1k
(x 1)
+=+
−
−=
−
⇒ 2
11
x1 xb
x1 (x 1)

+=− +

−−


⇒ 2
b
x2(1b)x(1b)0−+ ++=
(1)
y b = 0 : (1) trë thµnh −2x + 1 = 0 ⇔ 1
x2
=
y b ≠ 0 : (1) cã nghiÖm khi
2
'(1b) b(1b)0∆= + − + ≥ ⇔ b ≥ −1 (b ≠ 0)
Thµnh thö c¸c ®iÓm trªn Oy tõ ®ã cã thÓ ®−îc Ýt nhÊt mét tiÕp tuyÕn ®Õn ®å thÞ (C) lµ c¸c ®iÓm cã
tung ®é b ≥ −1.
3) Hoµnh ®é tiÕp ®iÓm cña parabol 2
yx a=+ víi ®å thÞ (C) lµ nghiÖm cña hÖ :
2o
2
1
xxa
x1
1
12x
(x 1)
+=+
−
−=
−
Tõ ph−¬ng tr×nh thø hai, suy ra :
2
x(2x 5x 4) 0−+= ⇒ x = 0.
Thay vµo ph−¬ng tr×nh ®Çu th× ®−îc a = - 1.
C©u II. §Æt S = x + y, P = xy, ta ®i ®Õn hÖ :
2
SP m
S2Pm
+=
−
=
1) Víi m = 5 ta ®−îc :
2
SP5
S2P5
+=
−=
⇒ P = 5 − S ⇒ 2
S2S150
+
−=
⇒ S = −5, S = 3.
Víi S = −5, ta cã P = 10, lo¹i v× ®iÒu kiÖn 2
S4P≥ kh«ng ®−îc nghiÖm ®óng.
Víi S = 3, ta cã P = 2 vµ ®−îc x2,
y1,
=
=
x1
y2.
=
=
2) Trong tr−êng hîp tæng qu¸t, P = m - S ⇒
2
S2S3m0+− =.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
___________________________________________________________
§Ó ph−¬ng tr×nh cã nghiÖm, cÇn ph¶i cã :
1
'13m0 m 3
∆= + ≥ ⇒ ≥− .
Khi ®ã gäi 1
S vµ 2
S lµ c¸c nghiÖm :
1
S113m=− − + , 2
S113m=− + + .
a) Víi 1
SS= ⇒ 1
PmS=−, ®iÒu kiÖn 2
S4P≥ trë thµnh
2
(1 13m) 4(m1 13m)++ ≥ +++ ⇒ (m 2) 2 1 3m−+≥ + ,
kh«ng ®−îc nghiÖm v× 1
m3
≥− ⇒ m + 2 > 0.
b) Víi 2
SS= ⇒ 2
PmS=−, ®iÒu kiÖn 2
S4P≥ trë thµnh :
2
( 1 1 3m) 4(m 1 1 3m)−+ + ≥ + − + ⇒ 21 3m m 2
+
≥+.
V× m + 2 > 0, cã thÓ b×nh ph−¬ng hai vÕ cña bÊt ph−¬ng tr×nh nµy vµ ®i ®Õn
2
0m 8m 0m8≥−⇒≤≤.
Cïng víi 1
m3
≥− suy ra ®¸p sè : 0 ≤ m ≤ 8.
C©u III. 1) HiÓn nhiªn víi x = 0 bÊt ph−¬ng tr×nh ®−îc nghiÖm víi mäi y. XÐt x > 0 ⇒
2
1x
cosy sin y 2x
+
+≥− .
Hµm f (y) = cosy + siny cã gi¸ trÞ lín nhÊt b»ng 2, gi¸ trÞ nhá nhÊt b»ng 2−, vËy ph¶i cã :
22
1x
2x22x10
2x
+
−≥− ⇒− +≥
⇒
⇒ 0x 21<≤ −, x21≥+.
XÐt x < 0 ⇒
2
1x
cosy sin y 2x
+
+≤− ⇒
⇒
22
1x
2x22x10x21
2x
+
≤− ⇒ + + ≥ ⇒ ≤− − ,
21x0−+≤<.
Tãm l¹i c¸c gi¸ trÞ ph¶i t×m lµ :
x21≤− − , 21x 21−+≤≤ −, 21x
+
≤
hay : |x| 2 1≥+ , |x| 2 1
≤
−
2) §iÒu kiÖn : xk
2
π
≠+π
( k ∈ Z). Chia hai vÕ cho 2
cos x ta ®−îc ph−¬ng tr×nh t−¬ng ®−¬ng :
22
tg x(tgx 1) 3tgx(1 tgx) 3(1 tg x)+= − + +
⇔ 2
tg x(tgx 1) 3(tgx 1) 0+− +=
⇔ 2
(tgx 1)(tg x 3) 0+−=
⇔ tgx 1
tgx 3
=−
=±
⇔
xk
4
xk
3
π
=− + π
π
=± + π
( k ∈ Z)
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________
C©u IVa. CÇn ®Ó ý r»ng c¸c ®ûêng th¼ng (D), (D’) vu«ng gãc víi nhau vµ chóng cã phû¬ng tr×nh tham sè
(D) : xbt
yat
=
=
(D’) : xat
ybt
=
=−
'
'
1) Thay biÓu thøc cña (D) vµo phû¬ng tr×nh cña (E), ta ®ûîc c¸c gi¸ trÞ cña tham sè t øng víi c¸c giao ®iÓm M, N. Tõ
®ã suy ra ch¼ng h¹n (do cã sù trao ®æi vai trß cña M, N):
M6b
9a + 4b
,6a
9a + 4b
,N - 6b
9a + 4b
,- 6a
9a + 4b
22 22 22 2
2
.
Tû¬ng tù:
P6a
4a + 9b
,- 6b
4a + 9b
,Q - 6a
4a + 9b
,6b
4a + 9b
22 22 22 2
2
.
2) Tø gi¸c MPNQ lµ h×nh thoi, víi diÖn tÝch
S = 2OM.OP = 72(a + b )
(9a + 4b )(4a + 9b )
22
2222
. (1)
3) §Ó ý r»ng c¸c phû¬ng tr×nh cña (D) vµ (D’) cã d¹ng thuÇn nhÊt (hay ®¼ng cÊp) ®èi víi a, b, tøc lµ thay cho a vµ b,
ta viÕt ka vµ kb víi k ¹0. Do vËy, cã thÓ coi r»ng a2+b2= 1. Khi ®ã (1) trë thµnh
S= 72
(4 + 5a )(4 + 5b )
=72
36 + 25a b
72
6= 12,
22 22
≤
dÊu=chØcãthÓxyrakhiab=0,tøclµhoÆca=0hoÆcb=0.(Khi ®ã cÆp ®ûêng th¼ng (D) vµ (D’) trïng víi cÆp hÖ trôc
täa ®é).
4) VÉn víi gi¶ thiÕt a2+b2= 1, theo trªn ta cã
S= 72
36 + 25a b
22
suyraminS=144
13 , x¶y ra khi |a| = |b|, tøc lµ cÆp ®ûêng th¼ng (D), (D’) lµ cÆp c¸c ph©n gi¸c y ⊄x = 0 cña hÖ
trôc täa ®é Oxy.
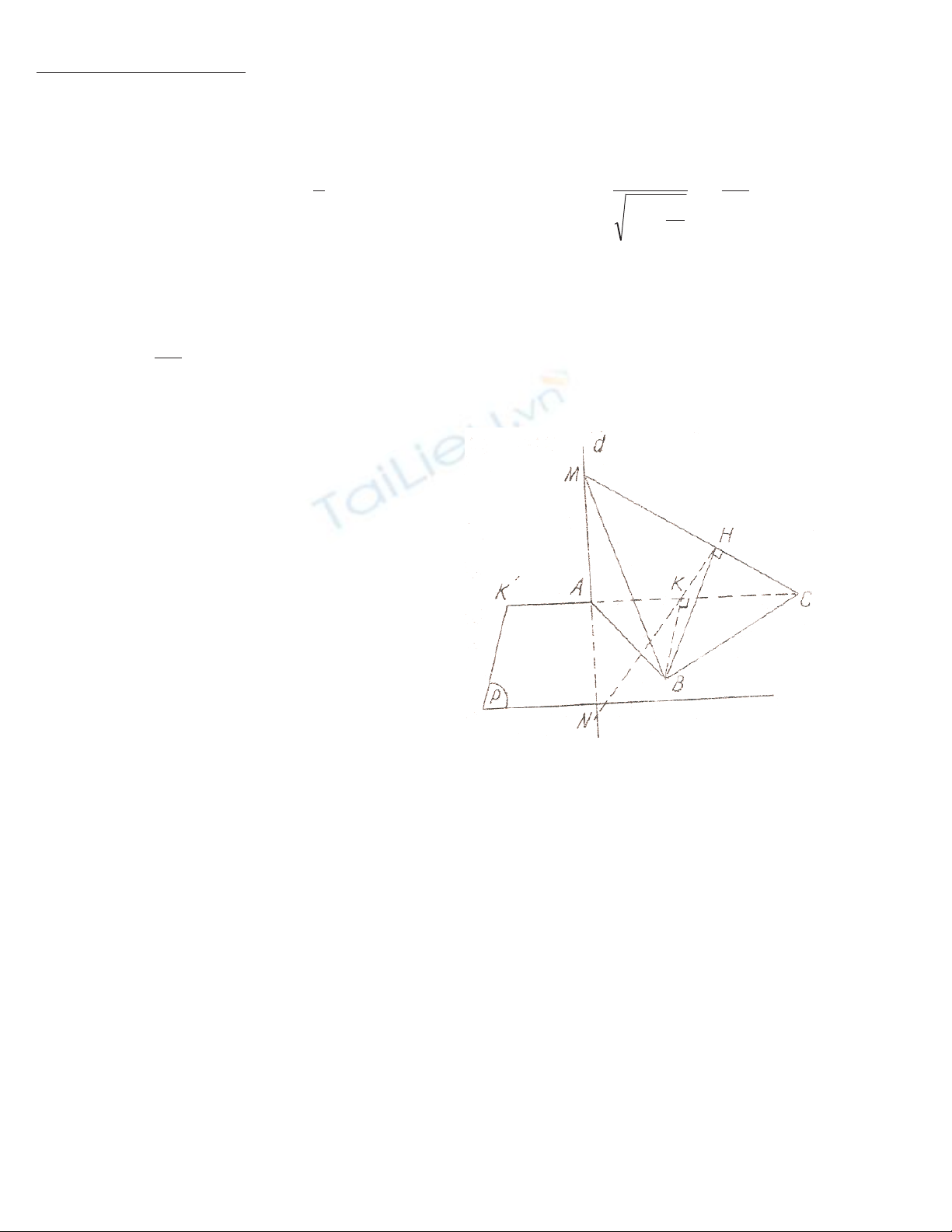
C©u IVb. (H×nh bªn)
1) BK ⊥AC, BK ⊥AM ÞBK ⊥(ACM) ÞBK ⊥CM.
Cïng víi BH ⊥CM, suy ra (BKH) ⊥CM ÞBN ⊥CM.
2) Do (BKH) ⊥CM ÞKH ⊥CM. VËy K lµ trùc t©m tam gi¸c CMN, vµ ta ®ûîc MK ⊥CN. Cïng víi BK ⊥CN Þ
(BMK)⊥CN ÞBM ⊥CN.
3) V× K lµ trùc t©m tam gi¸c CMN, nªn AM.AN = AK.AC
VËy khi M di chuyÓn trªn d, tÝch AM.AN kh«ng ®æi ÞMN==AM+ANnhánhÊt khi AM = AN. Khi ®ã
AM2= AK.AC, AM lµ ®ûêng cao trong tam gi¸c vu«ng CMK’, c¹nh huyÒn CK’, K’ lµ ®iÓm ®èi xøng cña K qua A.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________
V× 2|ab| £a2+b2= 1 suy ra a2b2£1
4, dÊu = chØ x¶y ra khi |a| = |b|, vËy S ³72
36 + 25
4
=144
13 ,