Trường đông Toán học - VTH 10/12/2014
ĐÁP ÁN ĐỀ THI
Ngày thi thứ hai
Thời gian: 180 phút
Bài 5 (7 điểm).Nếu pkhông là ước nguyên tố của bất kì annào thì ta có thể chọn
epbất kì và bài toán được chứng minh. Giả sử ngược lại, plà một ước nguyên tố của
ít nhất một trong các số an. Gọi klà số nguyên dương nhỏ nhất sao cho p|ak. Gọi
e=ep=số mũ của ptrong ak. Ta chứng minh rằng với mọi nthì hoặc p∤anhoặc
pe||an. (Kí hiệu pe||ancó nghĩa là pxuất hiện với số mũ etrong an).
Trước hết ta chỉ ra bằng qui nạp theo i≥1rằng
ak+i≡ai(mod p2e).
Viết
f(x) = c0+
d
X
j=2
cjxj=a1+x2 d
X
j=2
cjxj−2!,
(điều kiện f′(0) = 0 nói rằng luỹ thừa bậc nhất của xkhông xuất hiện trong khai
triển của f). Với i= 1 thì
ak+1 =f(ak) = a2
k X
j≥2
cjaj−2
k!+a1≡a1(mod p2e).
Như vậy, ak+1 ≡a1(mod p2e). Giả sử khẳng định đúng với i, nghĩa là ak+i≡ai
(mod p2e). Từ đó suy ra f(ak+i)≡f(ai) (mod p2e), hay ak+i+1 ≡ai+1 (mod p2e). Như
vậy theo nguyên lý qui nạp thì khẳng định được chứng minh.
Bây giờ cố định số nguyên dương nbất kì sao cho p|an. Viết n=kq +ivới
0≤i≤k−1. Giả sử i > 0. Thế thì ta có
an≡ak(q−1)+i≡ · · · ≡ ai(mod p2e).
Nói riêng, p|aivới i < k, nhưng điều này mâu thuẫn với cách chọn của k. Như vậy,
i= 0 và do đó n=kq. Thế nhưng đồng dư ở trên cũng nói rằng an≡ak(mod p2e).
Bởi vì pe||ak, đồng dư này cho thấy pe||an. Bài toán được chứng minh.
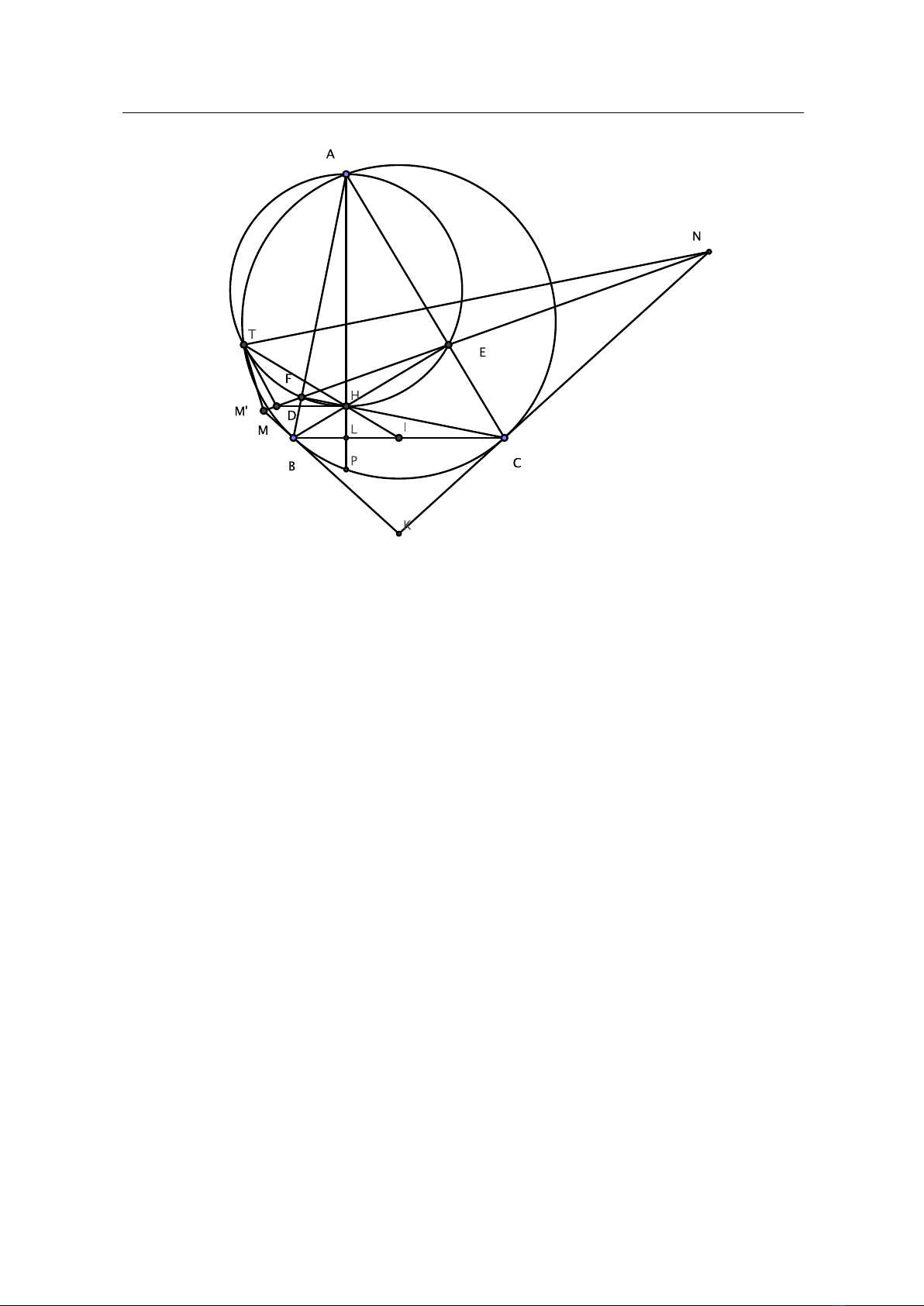
Bài 6 (7 điểm).(a) DT tiếp xúc (HEF ).
Trước tiên (HEF )là đường tròn đường kính AH (ký hiệu là [AH]) và theo tính
chất quen biết trong tam giác: "Đường thẳng HI đi qua giao điểm T′=Acủa (O)và
[AH]". Suy ra Tchính là giao điểm của (O)và [AH](T=A). Để ý rằng IF, IE chính
là các tiếp tuyến với [AH]nên tứ giác T F HE là tứ giác điều hòa. Do đó EF và các
tiếp tuyến tại Tvà Mđồng quy tại một điểm. Theo giả thiết, DH là tiếp tuyến tại M,
suy ra DT là tiếp tuyến tại T.
1
Trường đông Toán học - VTH 10/12/2014
(b) BM,CN ,T P đồng quy.
Trước hết, ta chứng minh BM là tiếp tuyến tại Bcủa (O). Giả sử tiếp tuyến tại
Bcắt EF tại M′. Để ý rằng các tam giác IF B và M′F B cân tại Ivà M′nên IM là
trung trực của F B. Suy ra \
IM′B+\
M′BF = 90∘. Dẫn đến
\
IM′B+[
ACB = 90∘.
Mặt khác, do [
BT A +[
ACB = 180∘và [
BT A =[
BT I + 90∘nên ta được
[
BT I +[
ACB = 90∘.
Từ đây suy ra \
IM′B=[
BT I nên M′thuộc đường tròn (IBT ). Theo cách dựng điểm
M, suy ra M′≡M. Vậy BM là tiếp tuyến tại Bcủa (O).
Tương tự CN cũng là tiếp tuyến của (O)tại C.
Gọi Klà giao điểm của BM và CN . Không khó chứng minh được ∆T BC ∼
∆T F E. Để ý rằng Klà giao điểm của các tiếp tuyến tại Bvà Ccủa (T BC)cũng như
Ilà giao điểm của các tiếp tuyến tại Fvà Ecủa (T F E). Suy ra các tứ giác T BKC
và T F IE đồng dạng. Suy ra \
BT K =d
F T I. Vì d
F T I =[
BAP nên \
BT K =[
BAP , thành
thử giao điểm của T K với (O)phải trùng với điểm P, nên T K đi qua P.
Vậy BM,CN và T P đồng quy.
Bài 7 (6 điểm).Ký hiệu
Pn(x) =
n
X
k=0
2k(n−k)xk.
Để chỉ ra đa thức Pn(x)có đúng nnghiệm thực, ta sẽ chỉ ra các số (= 0)
Pn(−2−n), Pn(−2−n+2), Pn(−2−n+4), . . . , Pn(−2n),
2
Trường đông Toán học - VTH 10/12/2014
luân phiên đổi dấu. Khi đó kết luận là hiển nhiên.
Với mỗi j= 0,1, . . . , n, nhóm các đơn thức trong đa thức Pn(x)thành các tổng có
dạng
Pn(x) = · · · +2(j−5)(n−j+5)xj−5+ 2(j−4)(n−j+4)xj−4
+2(j−3)(n−j+3)xj−3+ 2(j−2)(n−j+2)xj−2
+2(j−1)(n−j+1)xj−1+ 2j(n−j)xj+ 2(j+1)(n−j−1)xj+1
+2(j+2)(n−j−2)xj+2 + 2(j+3)(n−j−3)xj+3
+2(j+4)(n−j−4)xj+4 + 2(j−4)(n−j−5)xj+5 +· · · ,
Tùy vào tính chẵn lẻ của jvà n−j, có thể tổng đầu hoặc tổng cuối chỉ có một đơn
thức.
Bây giờ thế giá trị x=−2−n+2jvào biểu thức của đa thức Pn(x). Ta có
Pn(−2−n+2j) = · · · +(−1)j−4(−2j2−52+ 2j2−42)
+(−1)j−2(−2j2−32+ 2j2−22)
+0
+(−1)j+2(2j2−22−2j2−32)
+(−1)j+4(2j2−42−2j2−52) + · · ·
Chú ý rằng nếu có tổng đầu hoặc cuối là một đơn thức thì giá trị của đơn thức đó có
dấu là (−1)j. Sắp xếp lại ta suy ra
Pn(−2−n+2j) = (−1)j· · · +(2j2−42−2j2−52)
+(2j2−22−2j2−32)
+0
+(2j2−22−2j2−32)
+(2j2−42−2j2−52) + · · · .
Như vậy P(−2−n+2j)mang dấu của (−1)j. Hệ quả là các giá trị P(−2−n+2j)đổi dấu
liên tục khi jthay đổi từ 0,1, . . . , n.
3