Đáp Án Toán Khối D Năm 2006

Chia sẻ: Hà Yuki | Ngày: | Loại File: PDF | Số trang:4

Thêm vào BST

Báo xấu

7.236
lượt xem 228
download

Đáp Án Toán Khối D Năm 2006

Mô tả tài liệu

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo tài liệu 'đáp án toán khối d năm 2006', tài liệu phổ thông, ôn thi đh-cđ phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Bình luận(1) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đáp Án Toán Khối D Năm 2006

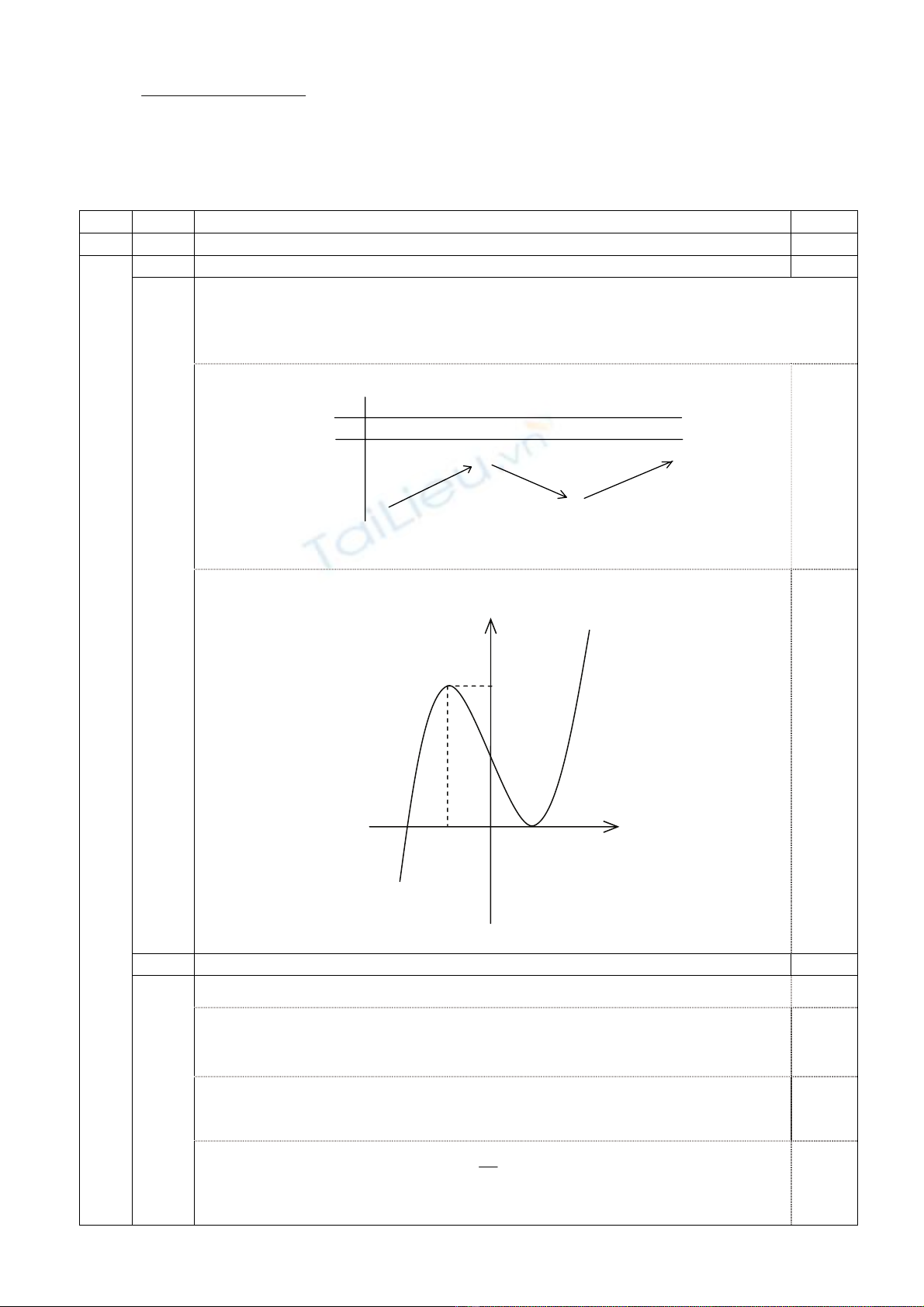
BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐÁP ÁN - THANG ĐIỂM KỲ THI TUYỂN SINH ĐẠI HỌC, CAO ĐẲNG NĂM 2006 ĐỀ CHÍNH THỨC Môn: TOÁN, khối D (Đáp án - Thang điểm có 04 trang) Câu Ý Nội dung Điểm I 2,00 1 Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1,00 điểm) y = x 3 − 3x + 2. • TXĐ: . • Sự biến thiên: y ' = 3x 2 − 3, y ' = 0 ⇔ x = − 1, x = 1. 0,25 Bảng biến thiên: x -∞ -1 1 +∞ y' + 0 _ 0 + 4 +∞ y 0 -∞ yCĐ = y ( −1) = 4, yCT = y (1) = 0. 0,50 • Đồ thị: y 4 2 −2 0,25 −1 O 1 x 2 Tìm m để d cắt (C) tại 3 điểm phân biệt (1,00 điểm) Phương trình đường thẳng d là: y = m ( x − 3) + 20. 0,25 Phương trình hoành độ giao điểm của d và ( C ) là: ( ) x 3 − 3x + 2 = m ( x − 3) + 20 ⇔ ( x − 3) x 2 + 3x + 6 − m = 0. 0,25 Đường thẳng d cắt đồ thị ( C ) tại 3 điểm phân biệt khi và chỉ khi 0,25 f ( x ) = x 2 + 3x + 6 − m có 2 nghiệm phân biệt khác 3 ⎧Δ = 9 − 4 ( 6 − m ) > 0 ⎧ 15 ⎪ ⎪m > ⇔ ⎨ ⇔ ⎨ 4 ⎪ ⎩ f ( 3) = 24 − m ≠ 0 ⎪m ≠ 24. 0,25 ⎩ 1/4
II 2,00 1 Giải phương trình (1,00 điểm) Phương trình đã cho tương đương với: − 2sin 2x.sin x − 2sin 2 x = 0 ⇔ sin x ( sin 2x + sin x ) = 0 0,50 ⇔ sin 2 x ( 2 cos x + 1) = 0. • sin x = 0 ⇔ x = kπ ( k ∈ ). 0,25 1 2π • cos x = − ⇔ x=± + k2π ( k ∈ ). 0,25 2 3 2 Giải phương trình (1,00 điểm) t2 +1 Đặt t = 2x − 1 ( t ≥ 0 ) ⇒ x = . Phương trình đã cho trở thành: 2 0,25 t 4 − 4t 2 + 4t − 1 = 0 ⇔ ( t − 1) 2 (t 2 ) + 2t − 1 = 0 ⇔ t = 1, t = 2 − 1. 0,50 Với t = 1, ta có x = 1. Với t = 2 − 1, ta có x = 2 − 2. 0,25 III 2,00 1 Tìm tọa độ điểm A ' đối xứng với A qua d1 (1,00 điểm) Mặt phẳng ( α ) đi qua A (1; 2;3) và vuông góc với d1 có phương trình là: 0,50 2 ( x − 1) − ( y − 2 ) + ( z − 3) = 0 ⇔ 2x − y + z − 3 = 0. Tọa độ giao điểm H của d1 và ( α ) là nghiệm của hệ: ⎧x − 2 y + 2 z −3 ⎧x = 0 ⎪ = = ⎪ ⎨ 2 −1 1 ⇔ ⎨ y = −1 ⇒ H ( 0; −1; 2 ) . 0,25 ⎪2x − y + z − 3 = 0 ⎩ ⎪z = 2 ⎩ Vì A ' đối xứng với A qua d1 nên H là trung điểm của AA ' ⇒ A ' ( −1; −4;1) . 0,25 2 Viết phương trình đường thẳng Δ (1,00 điểm) Vì Δ đi qua A, vuông góc với d1 và cắt d 2 , nên Δ đi qua giao điểm B của 0,25 d 2 và ( α ) . Tọa độ giao điểm B của d 2 và ( α ) là nghiệm của hệ: ⎧ x −1 y −1 z +1 ⎧x = 2 ⎪ = = ⎪ ⎨ −1 2 1 ⇔ ⎨ y = −1 ⇒ B ( 2; − 1; − 2 ) . 0,25 ⎪2x − y + z − 3 = 0 ⎩ ⎪z = − 2 ⎩ Vectơ chỉ phương của Δ là: u = AB = (1; −3; −5 ) . 0,25 x −1 y − 2 z − 3 Phương trình của Δ là: = = . 0,25 1 −3 −5 IV 2,00 1 Tính tích phân (1,00 điểm) 1 ⎧u = x − 2 ⎪ 1 I = ∫ ( x − 2 ) e2x dx. Đặt ⎨ 2x ⇒ du = dx, v = e2x . 0,25 0 ⎪dv = e dx ⎩ 2 1 1 1 1 I = ( x − 2 ) e 2x − ∫ e2x dx 0,25 2 0 20 1 e2 1 5 − 3e 2 = − + 1 − e 2x = . 0,50 2 4 0 4 2/4
2 Chứng minh với mọi a > 0, hệ phương trình có nghiệm duy nhất (1,00 điểm) Điều kiện: x, y > −1. Hệ đã cho tương đương với: ⎧e x + a − e x + ln (1 + x ) − ln (1 + a + x ) = 0 ⎪ (1) ⎨ ⎪y = x + a ⎩ ( 2) Hệ đã cho có nghiệm duy nhất khi và chỉ khi phương trình (1) có nghiệm duy 0,25 nhất trong khoảng ( − 1; + ∞ ) . Xét hàm số f ( x ) = e x + a − e x + ln (1 + x ) − ln (1 + a + x ) , với x > −1. Do f ( x ) liên tục trong khoảng ( − 1; + ∞ ) và lim f ( x ) = − ∞, lim f ( x ) = + ∞ x →−1+ x→ + ∞ nên phương trình f ( x ) = 0 có nghiệm trong khoảng ( − 1; + ∞ ) . 0,25 Mặt khác: 1 1 f ' ( x ) = ex + a − ex + − 1+ x 1+ a + x = ex ( ) ea − 1 + a (1 + x )(1 + a + x ) > 0, ∀x > −1. 0,25 ⇒ f ( x ) đồng biến trong khoảng ( − 1; + ∞ ) . Suy ra, phương trình f ( x ) = 0 có nghiệm duy nhất trong khoảng ( − 1; + ∞ ) . 0,25 Vậy, hệ đã cho có nghiệm duy nhất. V.a 1 Tìm tọa độ điểm M để đường tròn tâm M tiếp xúc ... (1,00 điểm) Đường tròn ( C ) có tâm I (1; 1) , bán kính R = 1. Vì M ∈ d nên M ( x; x + 3) . 0,25 Yêu cầu của bài toán tương đương với: 2 2 MI = R + 2R ⇔ ( x − 1) + ( x + 2 ) = 9 ⇔ x = 1, x = − 2. 0,50 Vậy, có hai điểm M thỏa mãn yêu cầu bài toán là: M1 (1; 4 ) , M 2 ( − 2; 1) . 0,25 2 Số cách chọn 4 học sinh thuộc không quá 2 trong 3 lớp (1,00 điểm) 4 Số cách chọn 4 học sinh từ 12 học sinh đã cho là C12 = 495. 0,25 Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau: - Lớp A có 2 học sinh, các lớp B, C mỗi lớp có 1 học sinh. Số cách chọn là: C5 .C1 .C1 = 120. 2 4 3 - Lớp B có 2 học sinh, các lớp C, A mỗi lớp có 1 học sinh. Số cách chọn là: C1 .C2 .C1 = 90. 5 4 3 0,50 - Lớp C có 2 học sinh, các lớp A, B mỗi lớp có 1 học sinh. Số cách chọn là: C1 .C1 .C3 = 60. 5 4 2 Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là: 120 + 90 + 60 = 270. Vậy, số cách chọn phải tìm là: 495 − 270 = 225. 0,25 3/4
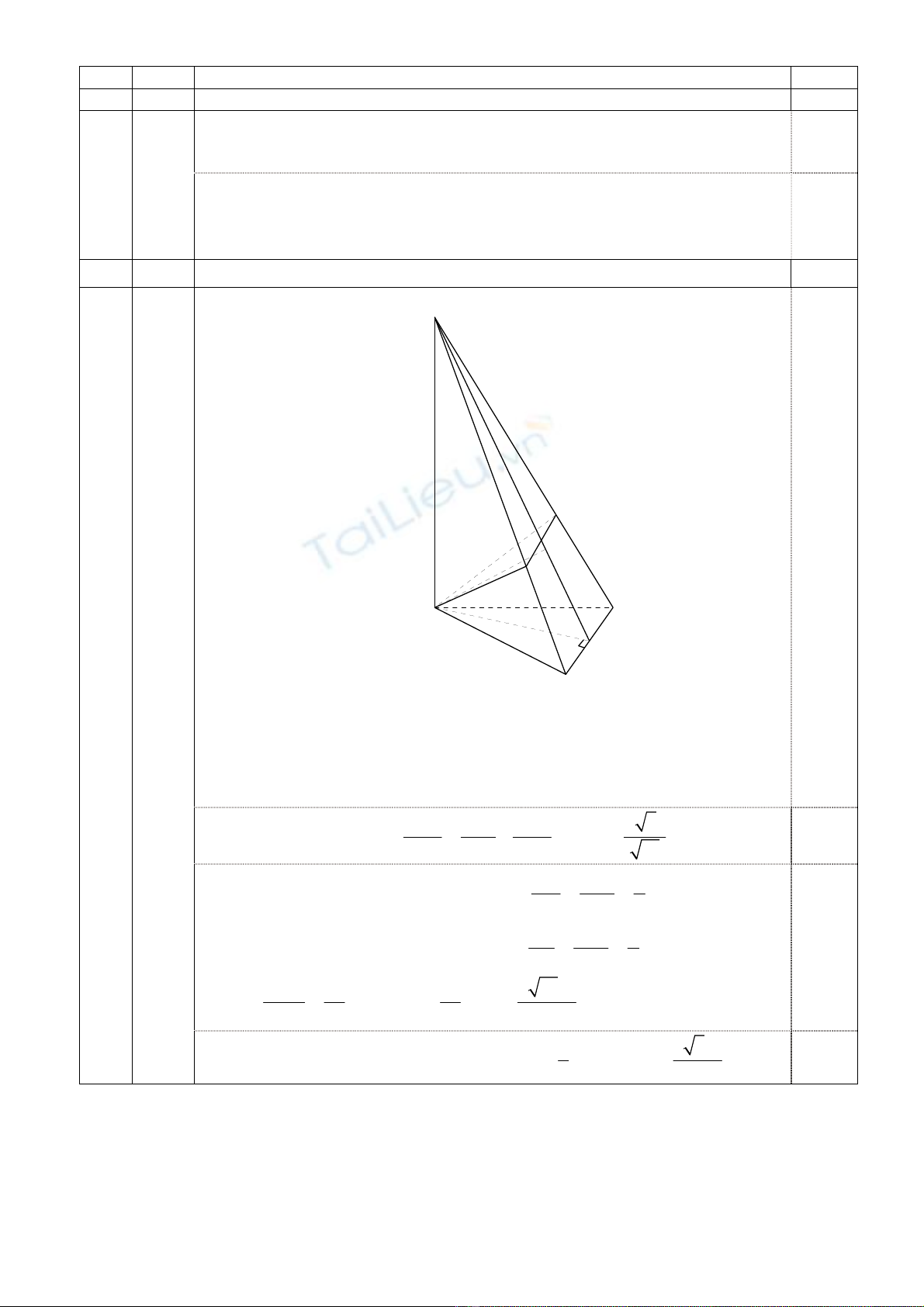
V.b 2,00 1 Giải phương trình (1,00 điểm) Phương trình đã cho tương đương với: ( 22x 2 x 2 −x ) ( − 1 − 4 2x 2 −x ) ( − 1 = 0 ⇔ 22x − 4 2 x )( 2 −x ) − 1 = 0. 0,50 • 22x − 4 = 0 ⇔ 22x = 22 ⇔ x = 1. 2 2 • 2 x − x − 1 = 0 ⇔ 2 x − x = 1 ⇔ x 2 − x = 0 ⇔ x = 0, x = 1. 0,50 Vậy, phương trình đã cho có hai nghiệm x = 0, x = 1. 2 Tính thể tích của khối chóp A.BCNM (1,00 điểm) S N H M A C K B Gọi K là trung điểm của BC, H là hình chiếu vuông góc của A trên SK. Do BC ⊥ AK, BC ⊥ SA nên BC ⊥ AH. 0,25 Do AH ⊥ SK, AH ⊥ BC nên AH ⊥ ( SBC ) . 1 1 1 2 3a Xét tam giác vuông SAK: 2 = 2 + 2 ⇒ AH = . 0,25 AH SA AK 19 SM SA 2 4 Xét tam giác vuông SAB: SA 2 = SM.SB ⇒ = = . SB SB2 5 SN SA 2 4 0,25 Xét tam giác vuông SAC: SA 2 = SN.SC ⇒ = = . SC SC2 5 S 16 9 9 19a 2 Suy ra: SMN = ⇒ SBCNM = SSBC = . SSBC 25 25 100 1 3 3a 3 Vậy, thể tích của khối chóp A.BCNM là: V = .AH.SBCNM = . 0,25 3 50 NÕu thÝ sinh lµm bµi kh«ng theo c¸ch nªu trong ®¸p ¸n mµ vÉn ®óng th× ®−îc ®ñ ®iÓm tõng phÇn nh− ®¸p ¸n quy ®Þnh. ---------------- Hết ---------------- 4/4