TRƯỜNG THCS LÊ QUANG CƯỜNG TỔ : TOÁN – TIN
HỆ THỐNG KIẾN THỨC TRỌNG TÂM GIỮA HKII – TOÁN 9 NĂM HỌC 2020-2021
I. Hệ phương trình bậc nhất hai ẩn
Hệ hai phương trình bậc nhất hai ẩn:
1. Dạng tổng quát : Trong đó (1) và (2) là những phương trìnnh bậc nhất 2ẩn.
2.Phương pháp giải: a/ Phương pháp thế.
b/ Phương pháp cộng đại số.
Giải bài toán bằng cách lập hệ phương trình.
- Chọn 2 ẩn và đặt điều kiện cho ẩn - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết - Lập hệ phương trình biểu thị mối liên hệ giữa các đại lượng
- Đồ thị hàm số y = ax2 (a≠0).
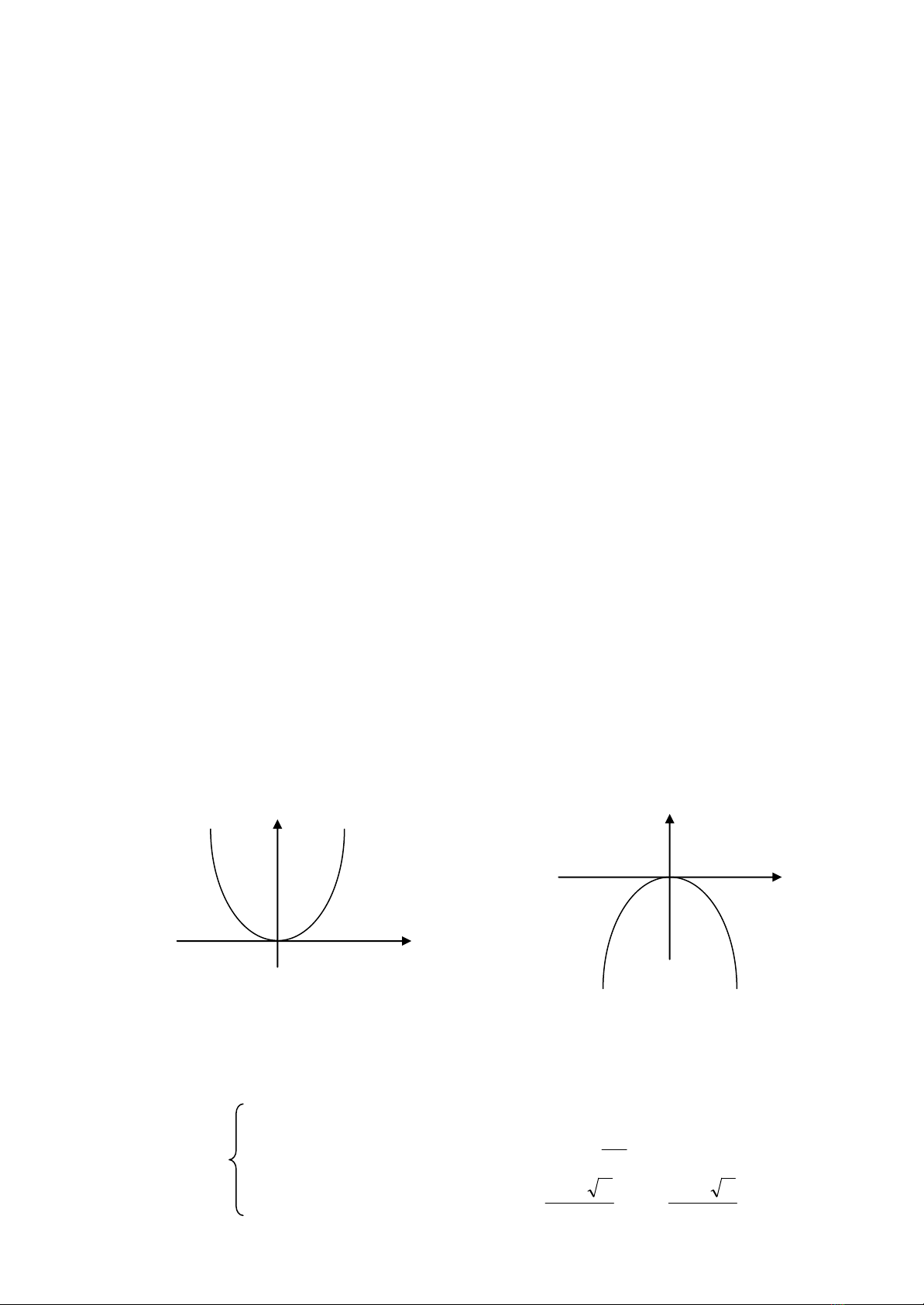
+ Bước1: Lập hệ phương trình. + Bước2: Giải hệ phương trình + Bước3: Đối chiếu với điều kiện của ẩn, trả lời bài toán. II. Hàm số y = ax2 (a≠0) - Phương trình bậc hai một ẩn 1. Tính chất của hàm số y = ax2 (a 0) - Nếu a>0 hàm số y = ax2 đồng biến khi x>0, nghịch biến khi x< 0 và bằng 0 khi x=0 - Nếu a< 0 hàm số y = ax2 đồng biến khi x<0, nghịch biến khi x< 0 và bằng 0 khi x= 0 2. Đồ thị hàm số y = ax2 ((aa 0) là một parabol có đỉnh là điểm O(0;0), nhận 0y là trục đối xứng.
- Nằm phía trên trục hoành và nhận điểm O(0;0) là điểm thấp nhất nếu a > 0 - Nằm phía dưới trục hoành và nhận điểm O(0;0) là điểm cao nhất nếu a < 0
X
y y
0
0 x
a > 0 a < 0
- Công thức nghiệm của phương trình bậc hai.
1) Định nghĩa: PT bậc hai một ẩn là pt có dạng ax2 + bx + c = 0 .Trong đó x là ẩn; a,b,c là
các hệ số đã cho ((aa 0) 2) Công thức nghiệm của phương trình bậc hai ax2+bx+c= 0 ((aa 0)
< 0 Phương trình vô nghiệm
= b2 - 4ac = 0 Phương trình có nghiệm kép: x1 = x2 =
> 0 PT có 2 nghiệm phân biệt: ;
*) Công thức nghiệm thu gọn của phương trình bậc hai ax2+bx+c= 0 với b = 2b'
'< 0 Phương trình vô nghiệm
'= b'2 - ac '= 0 Phương trình có nghiệm kép: x1 = x2 =
' > 0 PT có 2 nghiệm phân biệt: ;
III. Góc với đường tròn
1) Góc ở tâm:
+ ĐN: Là góc có đỉnh trùng với tâm của đường tròn + TC: Số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó Số đo cung lớn bằng 3600 trừ đi số đo cung nhỏ (có chung hai điểm mút)
2) Góc nội tiếp:
+ ĐN: Là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đò. + TC: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn + Hệ quả: Trong một đường tròn - Các góc nội tiếp bằng nhau chắn các cung bằng nhau - Các góc nội tiếp cùng chắn một cung hoặc hai cung bằng nhau thì bằng nhau - Các góc nội tiếp không quá 900 có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung. - Góc nội tiếp chắn nửa đường tròn là góc vuông.
3) Góc tạo bởi tia tiếp tuyến và dây cung:
+ TC: Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn. + Hệ quả: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau. 4) Góc có đỉnh ở trong và ngoài đường tròn: + Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo của hai cung bị chắn. + Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo của hai cung bị chắn.
II. Tứ giác nội tiếp
OA = OB = OC = OD
- Cách1: Chứng minh 4 điểm A, B, C, D cách đều một điểm O nào đó. - Cách 2: *Chứng minh tổng hai góc đối diện của tứ giác bằng 1800 hoặc + Định nghĩa: Một tứ giác có bốn đỉnh nằm trên một đường tròn thì được gọi là tứ giác nội tiếp đường tròn (đường tròn đó gọi là đường tròn ngoại tiếp của tứ giác). + Định lý: Trong một tứ giác nội tiếp, tổng số đo hai gúc đối diện bằng 1800. + Định lý đảo: Nếu một tứ giác có tổng số đo hai góc đối diện bằng 1800 thì tứ giác đó nội tiếp được một đường tròn. + Các cách chứng minh tứ giác ABCD nội tiếp: * Chứng minh góc trong bằng góc ngoài của đỉnh đối diện.
- Cách 3: Chứng minh 2 đỉnh liên tiếp của tứ giác cùng nhìn một cạnh dưới hai góc bằng nhau. - (Trường hợp đặc biệt hai đỉnh liên tiếp cùng nhìn một cạnh dưới 1 góc vuông thì cạnh đó chính là đường kính của đường tròn).
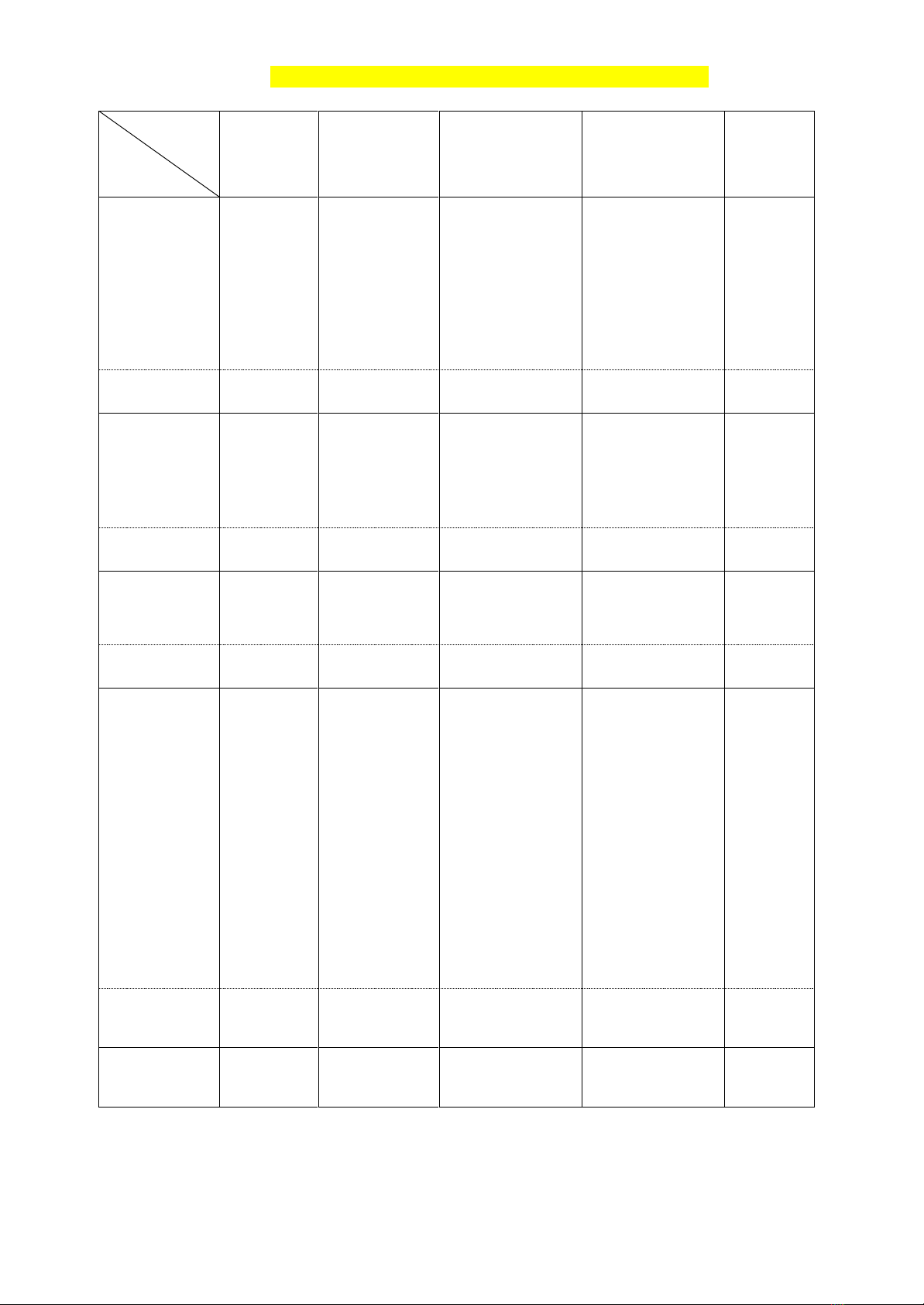
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ II TOÁN 9
Nhận biết Thông hiểu Vận dụng Vận dụng cao Cộng
Cấp độ Chủ đề 1.Hệ phương trình bậc nhất hai ẩn.
- Định m nguyên để hệ phương trình có nghiệm duy với nhất
-Giải được hệ phương trình bậc nhất hai ẩn. -Giải toán bằng cách lập hệ phương trình
nguyên.
3
1
3.5
0,5
Số câu: 4 Điểm: 4,0
Số câu: Số điểm 2.Phương trình bậc hai một ẩn.
1
- Dùng công thức nghiệm giải được phương trình bậc hai một ẩn.
Số câu:1 Điểm: 1,0
1,0 - Biết vẽ đồ thị của hàm số
Số câu Số điểm 3.Hàm số
1
1,5
Số câu: 1 Điểm: 1,5
.
Số câu Số điểm 4. Góc với đường tròn - Tính số đo cung, tính số đo góc.
-Chứng minh được tứ giác nội tiếp. -Chứng minh hệ thức. -Chứng minh các quan hệ song song, vuông góc, ...
2
1,5
0,5
Số câu: 5 Điểm: 3,5
7
2
2 1,0 Hình vẽ 0,5 2 1,5
7,5
1,0
-Chứng minh ba điểm thẳng hàng, đường thẳng đi qua điểm cố định, các đường đồng qui, cực trị hình học, ...... -Chứng minh , đoạn thẳng bằng nhau, góc bằng nhaucác quan hệ song song, vuông góc, ... 1 Số câu Số điểm
Tổng số câu Tổng số điểm
