Đ C NG ÔN T P MÔN TOÁN L P 9 HKIIỀ ƯƠ Ậ Ớ
I. TR C NGHI MẮ Ệ :
A. ĐI S :Ạ Ố
1. N u đ th c a hàm s y = axế ồ ị ủ ố 2 đi qua đi m (-1; 3) thì h s a là:ể ệ ố
a. -1 b. 1 c. 3 d. -3
2. Cho hàm s ố
2
1
2
y x= −
. câu tr l i nào sai?ả ờ
a. Đ th c a hàm s đã cho đi x ng qua tr c tung.ồ ị ủ ố ố ứ ụ
b. Đ th c a hàm s đã cho n m phía d i tr c hoành.ồ ị ủ ố ằ ướ ụ
c. Hàm s ngh ch bi n khi x < 0 và đng bi n khi x > 0.ố ị ế ồ ế
d. Giá tr l n nh t c a hàm s b ng 0 khi x = 0.ị ớ ấ ủ ố ằ
3. Đi v i hàm s ố ớ ố
( )
2
0y ax a= ﾹ
, n u a >0 và x >0 thì hàm s :ế ố
a) Ngh ch bi n;ị ế b) Đng bi n;ồ ế c) a và b đúng; d) a và b sai.
4. Đ th hàm s ồ ị ố
2
3y x=
có v trí nh th nào đi v i tr c hoành:ị ư ế ố ớ ụ
a) Phía trên; b) Phía d i;ướ c) C t;ắd) Song song.
5. Ph ng trình ươ
2
3 0x+ =
có nghi m là:ệ
a)
3x= -
; b)
3x=
; c)
0x=
; d) Vô nghi m.ệ
6. Ph ng trình ươ
2
5 7 0x x- - =
có s nghi m là:ố ệ
a) 2 nghi m phân bi t;ệ ệ b) nghi m kép;ệc) Vô nghi m;ệd) Vô s nghi m.ố ệ
7. G i xọ1 và x2 là hai nghi m c a ph ng trình ệ ủ ươ
( )
2
0 0ax bx c a+ + = ﾹ
. Theo h th c Vi-ét ta ệ ứ
có:
a)
1 2
b
x x a
ﾹ
+ = -
; b)
; c)
1 2
2
b
x x a
+ = -
; d)
1 2
2
b
x x a
ﾹ
+ = -
8. Trong công th c nghi m thu g n, có:ứ ệ ọ
a)
2
4b ac
ﾹ= -V
; b)
2
b a c
ﾹ ﾹ
= -V
; c)
2
b ac
ﾹ ﾹ
= -V
; d)
2
4b ac= -V
.
9. H ph ng trình ệ ươ
2 1
4 2 2
x y
x y
ﾹ - =
ﾹ
ﾹ
ﾹ
ﾹ- = -
ﾹ
ﾹ
có s nghi m là bao nhiêu?ố ệ
a) 1 nghi m;ệb) 2 nghi m;ệc) Vô s nghi m;ố ệ d) Không có nghi m.ệ
10. C p s ặ ố
( )
2;1-
là nghi m c a ph ng trình nào sau đây:ệ ủ ươ
a)
2 0x y+ =
; b)
2 1x y- =
; c)
3 5x y- = -
; d) C a và c.ả
11. Ph ng trình b c nh t hai n ươ ậ ấ ẩ
ax by c+ =
luôn có:
a) Nghi m duy nh t;ệ ấ b) Vô s nghi m;ố ệ c) Không có nghi m; ệd) Ch có m t nghi m.ỉ ộ ệ
12. Trong các ph ng trình sau, ph ng trình nào có hai nghi m phân bi t?ươ ươ ệ ệ
a. x2 + x + 1 b. x2 + 4 = 0 c. 2x2 – 3x – 1 d. 4x2 – 4x + 1
13. Hai s 6 và – 4 là nghi m c a ph ng trình nào sau đây?ố ệ ủ ươ
a. x2 – 6x – 4 =0 b. x2 + 2x – 24 =0 c. x2 – 2x – 25 d. x2 - 2x – 24
14. Ph ng trình nào sau đây vô nghi m?ươ ệ
a. 2x2 – 4 =0 b. x2 – 6x =0 c. 3x2 + x – 1 =0 d. x2 – 4x + 5 = 0.
15. Xét s đng bi n và ngh ch bi n c a hàm s sau: y = -5xự ồ ế ị ế ủ ố 2.
a. Hàm s ngh ch bi n trên Rố ị ế b. Hàm s đng bi n trên R.ố ồ ế
c. Hàm s đng bi n khi x < 0 và ngh ch bi n khi x > 0. ố ồ ế ị ế
d. Hàm s ngh ch bi n khi x <0 và đng bi n khi x >0,ố ị ế ồ ế
16. Cho hàm s F(x) = y = axố2. Bi t đ th c a hàm s đi qua đi m A(-4: 8). Khi h s a đc ế ồ ị ủ ố ể ệ ố ượ
tính là:
a. 2 b. 4 c.
1
2
d.
1
4
17. Đ th c a hàm s y = - xồ ị ủ ố 2. có v trí nh th nào so v i tr c hoành:ị ư ế ớ ụ
a) Phía trên; b) Phía d i;ướ c) C t;ắd) Song song.
18. Ph ng trình 3xươ 2 + 12 = 0, có nghi m là:ệ
a. x = -4 b. x =
2 c. Vô nghi m.ệd. Đáp án khác.
19. Ph ng trình b c hai: 3xươ ậ 2 + 6x - 9 =0, có nghi m là:ệ
a. x = 1; x = 3 b. x = 1; x = -3 c. x = -1; x = 3 d. x = -1; x = -3
20. H ph ng trình ệ ươ
2 1
4 2 2
x y
x y
ﾹ - =
ﾹ
ﾹ
ﾹ
ﾹ- = -
ﾹ
ﾹ
có s nghi m là bao nhiêu?ố ệ
a) 1 nghi m;ệb) 2 nghi m;ệc) Vô s nghi m;ố ệ d) Không có nghi m.ệ
21. Trong các c p s sau đây, c p s nào là nghi m c a h ph ng trình ặ ố ặ ố ệ ủ ệ ươ
3 3
2 7
x y
x y
ﾹ
ﾹ+ =
ﾹ
ﾹ
ﾹ- =
ﾹ
ﾹ
?
a)
( )
0; 0
b)
( )
2; 3-
; c)
( )
1;2
; d)
( )
0;1
22. H ph ng trình ệ ươ
( )
, , , , , 0
ax by c
a b c a b c
a x b y c
ﾹ+ =
ﾹ
ﾹ
ﾹﾹ ﾹ ﾹ ﾹ
ﾹﾹ ﾹ ﾹﾹ + =
ﾹ
ﾹ
ﾹ
có vô s nghi m n u:ố ệ ế
a)
a b c
a b c
= =
ﾹ ﾹ ﾹ
; b)
b c
b c
ﾹ
ﾹ ﾹ
; c)
a b c
a b c
= ﾹ
ﾹ ﾹ ﾹ
; d)
a b
a b
ﾹ
ﾹ ﾹ
.
23. Tìm m đ ph ng trình xể ươ 2 – 2x + m + 1 = 0, có hai nghi m phân bi t:ệ ệ
a. m > 1 b. m < 1 c. m < 0 d. m > 0
24. Tìm m đ ph ng trình 2xể ươ 2 -
3
x – m = 0, có nghi m:ệ
a. m <
3
8
−
b. m >
3
8
−
c. m
3
8
−
d. m
3
8
−
.
25. Trong các ph ng trình sau, ph ng trình nào có hai nghi m phân bi t?ươ ươ ệ ệ
a. 3x2 – 6 = 0 b. 3x2 + 8x = 0 c. 4x2 – x – 1 = 0 d. C a, b, c.ả
26. V i giá tr nào c a a thì đng th ng (d): y = x + a ti p xúc v i parabol (P): y = xớ ị ủ ườ ẳ ế ớ 2?
a. -1 b. 1 c.
1
4
−
d.
1
4
27. Ph ng trình nào sau đây có nghi m kép?ươ ệ
a. 3x2 – 5x = 0 b. 9x2 – 12x + 4 = 0 c. 3x2 + 5 = 0 d. x2 – 4x + 3 = 0.
28. T a đ giao đi m c a (d): y = 2x – 3 và (P): y = - xọ ộ ể ủ 2 là:
a. (1; -1) và (-3; -9) b. (-1; -1) và (-3; 9) c. (1; -1) và (3;9) d. (-1;-1) và (3;-9)
29. V i giá tr nào c a m thì ph ng trình xớ ị ủ ươ 2 – 5x + 4m – 3 = 0, có hai nghi m phân bi t:ệ ệ
a. m <
37
16
b. m >
37
16
c. m
37
16
d. m
37
16
.
30. V i giá tr nào c a m thì ph ng trình xớ ị ủ ươ 2 – 6x + 1 – 3m = 0, có hai nghi m phân bi t:ệ ệ
I
B
C
A
a. m >
8
3
−
b. m
8
3
−
c. m =
8
3
−
d. m = -3
B. HÌNH H C:Ọ
31.Cho
∆
ABC n i ti p đng tròn (O), bi t  = 70ộ ế ườ ế 0,
ﾹ
0
40C=
, câu nào sau đây sai?
a. sđ
ﾹ
AB
= 800b.
ﾹ
ﾹ
AC BC=
c.
ﾹ
ﾹ
AOC=BOC
d.
ﾹ
0
AOC=70
.
32. Trên đng tròn (O) l y theo th t 4 đi m A, B, C, D sao cho sđườ ấ ứ ự ể
ﾹ
AB
= 1000, sđ
ﾹ
0
BC 60=
, sđ
ﾹ
0
CD 130=
. Cách s p x p nào sau đây đúng?ắ ế
a. AB >BC>CD>DA b. AB>BC>DA>CD c. CD>AB>DA>BC d. CD>AB>BC>DA
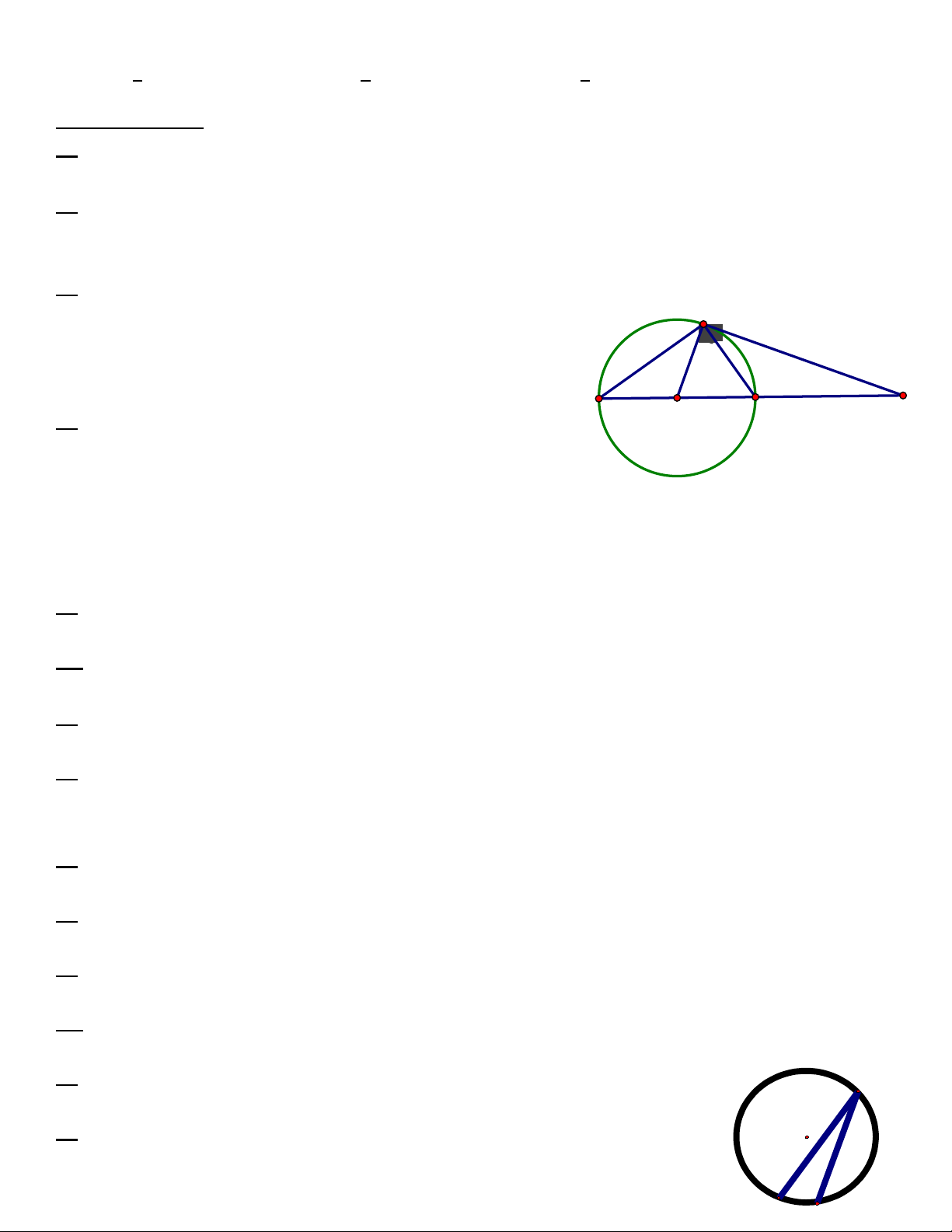
33. Xem hình, s đo c a góc BAI là bao nhiêu, bi t sđố ủ ế
ﾹ
AC
= 2 sđ
ﾹ
AB
:
a. 400
b. 300
c. 600
d. 500
34. Cho đng tròn (O; R)ườ
và dây cung AB = R. trên cung nh AB l y ỏ ấ
đi m M. S đo góc AMB là:ể ố
a. 600 b. 900c. 1500d. 1200
* Tr l i câu 36, 37 v i gi thi t bài toán sau:ả ờ ớ ả ế
Cho đng tròn (O; R) đng kính AB, M là đi m trên đng tròn sau cho góc MAB b ng 30ườ ườ ể ườ ằ 0,
ti p tuy n t i M c a (O) c t đng th ng AB t i S.ế ế ạ ủ ắ ườ ẳ ạ
36. Góc
ﾹ
MSA
có s đo là bao nhiêu?ố
a. 300b. 450c. 600d. 900.
37. Câu nào sau đây sai?
a.
ﾹ
0
AMB 90=
b.
∆
MAS cân t i Mạc.
∆
SMB ∽
∆
SAM d. sđ
ﾹ
0
60=AM
.
38. Cho đng tròn (O), hai dây cung AB, AC sao cho góc BAC b ng 50ườ ằ 0. V y sđậ
ﾹ
BC
là:
a. 1000b. 2600c. 1300d. 500
39. Ch n câu sai. T giác ABCD n i ti p đc đng tròn khi:ọ ứ ộ ế ượ ườ
a.
ﾹ
ﾹ
0 0
DAB=120 ;BCD=60
b.
ﾹ
ﾹ
DAC=DBC
c.
ﾹ
ﾹ
0
ADC+BCD=180
d. ABCD là hình thang cân.
40. Cho đng tròn (O; 6cm) và cung AB có s đo b ng 80ườ ố ằ 0. Đ dài cung l n AB là:ộ ớ
a. 29,31cm b. 28,16cm c. 28,84cm d. 29,01cm
41. Di n tích hình tròn là 64ệ
π
cm2. V y chu vi c a đng tròn đó là:ậ ủ ườ
a. 20
π
cm b. 16
π
cm c. 15
π
cm d. 12
π
cm.
42. M t hình tròn có chu vi là 18,84 cm thì di n tích hình tròn là: ộ ệ
a. 30,20cm2b. 28,84cm2c. 28,26cm2d. 27,64cm2.
43. Di n tích hình vành khăn gi i h n b i hai đng tròn (O; 10cm) và (O; 6cm) là:ệ ớ ạ ở ườ
a. 64
π
cm2b. 60
π
cm2c. 72
π
cm2d. M t đáp s khác.ộ ố
44. Đ dài c a cung tròn 68ộ ủ 0 c a m t đng tròn có bán kính 10cm:ủ ộ ườ
a) 9,86; b) 10,86; c) 11,87. d) 11,86;
45. Công th c tính di n tích hình qu t tròn bán kính R, cung nứ ệ ạ 0 là:
A
B
C
200
a)
2
360
R n
p
; b)
2
R
p
; c)
180
R n
p
d)
360
R n
p
; .
46. Quan sát hình v , sđẽ
?
BC
=
a) 600b) 400; c) 200; d) 300.
47. Di n tích hình vành khăn c a hai đng tròn đng tâm bán kính Rệ ủ ườ ồ 1 và R2 (R1>R2) là
a)
( )
2 2 2
1 2
R R
p
-
; b)
( )
2 2
1 2
R R
p
-
c)
( )
2 2
2 1
R R
p
-
d)
2 2
1 2
R R
p
.
48. Di n tích m t c u có bán kính 5cm là:ệ ặ ầ
a. 628cm2b. 314cm2c. 942cm2d. 471cm2
49. Hình tr Sụxq= 452,16mm2, chi u cao là 12mm. V y bán kính c a hình tròn đáy là?ề ậ ủ
a. 2cm b. 3cm c. 4cm d. 6cm
50. M t hình nón có Sộxq=37,68cm2 và bán kính đng tròn đáy là 3cm. Đ dài đng sinh là:ườ ộ ườ
a. 3cm b. 4cm c. 5cm d. 6cm
51. M t hình tr có th tích 2826cmộ ụ ể 3, chi u cao c a hình tr là 25cm. Di n tích đáy là:ề ủ ụ ệ
a. 131,04cm2b. 113,04cm2c. 134,01cm2d. 143,10cm2
52. M t hình c u có th tích là 7134,56cmộ ầ ể 3. V y bán kính hình c u là:ậ ầ
a. 15cm b. 13cm c. 12cm d. 10cm
II.T LU N:Ự Ậ
A. ĐI S :Ạ Ố
Bài 1: Gi i h ph ng trình sau:ả ệ ươ
2 3 5 5 4 3 2 3 2 4
) ) ) )
2 2 3 3 2 5 3 2 3 7
− = − = + = + =
+ = + = − = − =
x y x y x y x y
a b c d
x y x y x y x y
Bài 2: Gi i ph ng trình sau:ả ươ
a) x2 – 6x – 4 = 0 b)x2 + 2x – 24 = 0 c) 3x2 – 6x = 0
d) 2x2 – 18 = 0 e) x4 – 5x2 + 4 = 0 f) x2 – 4x + 5 = 0
Bài 3: Cho ph ng trình -xươ 2 + 2(m-1)x – m2 = 0
a) Gi i ph ng trình v i m = 2ả ươ ớ
b) Tìm m đ ph ng trình có nghi m ?ể ươ ệ
c) Tìm m đ ph ng trình có 2 nghi m xể ươ ệ 1, x2 th a mãn ỏ
1 2
x x 2− =
Bài 4: Cho parabol (P): y = ax2 và đng th ng (d): y = kx +3.ườ ẳ
a) Xác đnh a và k, bi t t a đ giao đi m c a parabol và đng th ng là A(3; 18).ị ế ọ ộ ể ủ ườ ẳ
b) T k t qu câu a) tìm giao đi m th hai c a (P) và (d).ừ ế ả ể ứ ủ
Bài 5: M t ng i d đnh đi xe đp t A đn B cánh nhau 30 km v i v n t c không đi. Tuy ộ ườ ự ị ạ ừ ế ớ ậ ố ổ
nhiên sau khi đi đc n a đng vì s c nên ng i này ph i d ng l i 20 phút, do đó ph i ượ ử ườ ự ố ườ ả ừ ạ ả
tăng v n t c lên thêm 3km/h và đn B ch m h t 10 phút. Tính v n t c d đnh ban đu c a ậ ố ế ậ ế ậ ố ự ị ầ ủ
ng i y?ườ ấ
Bài 6: Tính chu vi hình ch nh t, bi t dài g p hai l n chi u r ng và di n tích là 800mữ ậ ế ấ ầ ề ộ ệ 2.
Bài 7: Hai xe kh i hành cùng m t lúc t A đn B cách nhau 100 km, xe th nh t ch y nhanh ở ộ ừ ế ứ ấ ạ
h n xe th hai 10 km/h nêm đã đn s m h n 30 phút. Tính v n t c m i xe?ơ ứ ế ớ ơ ậ ố ỗ
B. HÌNH H C:Ọ
Bài 11: Cho tam giác ABC n i ti p đng tròn (O), đng cao AH, AD là đng kính, E là ộ ế ườ ườ ườ
đi m chính gi a cung BC không ch a đi m A. Ch ng minh r ng:ể ữ ứ ể ứ ằ
a)
ﾹ
ﾹ
BAH=CAD
b)
ﾹ
ﾹ
BAD=CAH
c) AE là tia phân giác c a góc HAD.ủ
Bài 12: Cho n a đng tròn (O) đng kính AB. Bi t AB = 8cm, dây AC t o v i AB m t góc ử ườ ườ ế ạ ớ ộ
300. Tia ti p tuy n Bx k t i B v i đng tròn (O) c t AC t i D. Trên tia Bx l y đi m E sao ế ế ẻ ạ ớ ườ ắ ạ ấ ể
cho BE = BA.
a) Ch ng minh AD = 2BDứ
b) G i F là giao đi m th hai c a AE v i n a đng tròn. Ch ng minh F là trung đi m c a ọ ề ứ ủ ớ ử ườ ứ ể ủ
AE.
c) Ch ng minh AF.AE = AC.AD.ứ
Bài 13: Cho n a đng tròn đng kính AB. T A và B k hai ti p tuy n Ax và By. Qua đi mử ườ ườ ừ ẻ ế ế ể
M thu c n a đng tròn này, k ti p tuy n th ba, c t các ti p tuy n Ax và By l n l t E ộ ử ườ ẻ ế ế ứ ắ ế ế ầ ượ ở
và F, AM c t OE t i P.ắ ạ
a)Ch ng minh t giác AEMO và t giác MPHO n i ti p.ứ ứ ứ ộ ế
b) G i BM c t OF t i Q. T giác MPOQ là hình gì ? T i sao?ọ ắ ạ ứ ạ
c) K MH vuông góc v i AB (H thu c AB). G i K là giao đi m c a MH và EB. ẻ ớ ộ ọ ể ủ
Ch ng minh MK = KH.ứ
Bài 14: T đi m M n m ngoài đng tròn (O) v hai ti p tuy n MA, MB v i đng tròn (O)ừ ể ằ ườ ẽ ế ế ớ ườ
(A và B là hai ti p đi m)ế ể
a) Ch ng minh t giác MAOB n i ti pứ ứ ộ ế
b) T M k cát tuy n MCD v i đng tròn (C n m gi a M và D), tia MD n m gi a hai tiaừ ẻ ế ớ ườ ằ ữ ằ ữ
MA và MO. Tia MO c t AB t i H. Ch ng minh: MC. MD = MH. MOắ ạ ứ
c) Qua C k đng th ng song song v i AD c t AM t i I, c t AB t i K. Ch ng minh C làẻ ườ ẳ ớ ắ ạ ắ ạ ứ
trung đi m c a IK.ể ủ
C. B T ĐNG TH C VÀ C C TRẤ Ẳ Ứ Ự Ị
Bài 1.
a)Cho a,b > 0. Ch ng minh ứ
1 1 4
a b a b
+ +
b)Cho a,b,c >0 th a mãn ỏ
1 1 1
abc
+ +
= 4. Tìm giá tr l n nh t c a bi u th cị ớ ấ ủ ể ứ
M =
1 1 1
2 2 2a b c a b c a b c
+ +
+ + + + + +
Bài 2.
a) Cho a, b là hai s th c d ng tùy ý. Ch ng minh r ng : ố ự ươ ứ ằ
2
a b
b a
+
D u “=” x y ra khi nào?ấ ả
b) Cho a, b, c là đ dài ba c nh c a m t tam giác. Tìm giá tr nh nh t c a bi u th c:ộ ạ ủ ộ ị ỏ ấ ủ ể ứ
4a 9b 16c
P = + +
b + c - a a + c - b a + b - c
Bài 3. Cho a, b, c > 0. Ch ng minh:ứ