Tr ng THCS Thăng Longườ T Toán – Líổ
Đ C NG ÔN T P THI H C K IIỀ ƯƠ Ậ Ọ Ỳ
Môn : Toán 8
Năm h c : 2017-2018ọ
A/ LÝ THUY T : ẾÔn l i toàn b lý thuy tạ ộ ế
1. Th nào là hai ph ng trình t ng đng ? Hai phế ươ ươ ươ ng trình cùng vô nghi m có t ng ươ ệ ươ
đng không?ươ
2. Đnh nghĩa ph ng trình b c nh t m t n , nêu s nghi m c a ph ng trình b c nh t ị ươ ậ ấ ộ ẩ ố ệ ủ ươ ậ ấ
m t n ? S nghi m c a ph ng trình có d ng ax + b = 0? ộ ẩ ố ệ ủ ươ ạ
3. Th nào là hai b t ph ng trình t ng đng ? Cho VD minh hoế ấ ươ ươ ươ ạ
4. Đnh nghĩa b t ph ng trình b c nh t m t n . ị ấ ươ ậ ấ ộ ẩ Cho VD minh hoạ
5. Nêu các qui t c bi n đi ph ng trình và các qui t c bi n đi b t ph ng trình .ắ ế ổ ươ ắ ế ổ ấ ươ
6. Phát bi u đnh lý Talet ( thu n , đo và h qu ) , v hình và ghi gt – kl .ể ị ậ ả ệ ả ẽ
7. Phát bi u đnh lý v tính ch t đng phân giác trong tam giác , v hình và ghi gt – kl.ể ị ề ấ ườ ẽ
8. Phát bi u đnh nghĩa và đnh lý v tam giác đng d ng , v hình và ghi gt – klể ị ị ề ồ ạ ẽ
9. Phát bi u ba tr ng h p đng d ng c a tam giác , v hình và ghi gt – klể ườ ợ ồ ạ ủ ẽ
10. Hai tam giác đng d ng theo t s k, nêu t s c a hai đng cao t ng ng, hai trung ồ ạ ỉ ố ỉ ố ủ ườ ươ ứ
tuy n t ng ng, hai chu vi, hai di n tích c a hai tam giác đó.ế ươ ứ ệ ủ
11. Nêu công th c tính di n tích xung quanh, di n tích toàn ph n và th tích c a hình lăng ứ ệ ệ ầ ể ủ
tr đng, hình h p ch nh t, hình l p ph ng, hình chóp đu.ụ ứ ộ ữ ậ ậ ươ ề
B/ BÀI T P : Ậ
I. ĐI S .Ạ Ố
Gi i ph ng trình và b t ph ng trình.ả ươ ấ ươ
Bài 1 : Gi i ph ng trìnhả ươ
a) – 5x + 1 = 0 d)
1 2 5 3
3 6
x x- -
- =
b) 5( x2 – 2x) = ( 3 + 5x) (x – 1) e) ( 4x + 3 )2 = 4( x - 1)2
c) (3-x)2 – 12 + 4x = 0 g) ( 4x - 5 )2 - 2 ( 16x2 - 25 ) = 0
Bài 2 : Gi i ph ng trìnhả ươ
a)
5
2
42
1
23
x
x
x
x
c )
0
1
2
1
34
2
xx
x
b)
2
1 1 1 10 3
8 16 2 ( 2) 8 16
x x
x x x x x x
− −
− = −
− − −
d)
34
8
3
1
1
5
2
xxx
x
x
x
g) 5x-1- 2x = 7 h) 8 - x= x2 + x
Bài 3 : Gi i b t ph ng trình và bi u di n t p nghi m trên tr c s :ả ấ ươ ể ễ ậ ệ ụ ố
a) 2,4x – 17,2 > 14,8 – 5,6x b)
3
3
5
4
1
x
x
x
c)
8 1 9 1 12 1
4 3 12
x x x
+ + +
< −
d)
2
6
12
3
1
1
xx
e) ( x - 1)( x+ 2) ≥ (x-1) 2 + 3 g) x2 – x – 2 ≤ 0
Gi i bài toán b ng cách l p ph ng trình ả ằ ậ ươ
Bài 4. M t ng i đi xe đp t A đn B v i v n t c 12km/h . Lúc v ng i đó đi đng khác ộ ườ ạ ừ ế ớ ậ ố ề ườ ườ
ng n h n lúc đi 22km và đi v i v n t c 10km/h nh ng th i gian v v n ít h n th i gian đi là ắ ơ ớ ậ ố ư ờ ề ẫ ơ ờ
1h20’. Tính quãng đng AB. ườ
Bài 5. Lúc 7gi m t ng i đi xe máy t A đn B v i v n t c 40km/h. Lúc 8h30phút cùng ngày ờ ộ ườ ừ ế ớ ậ ố
m t ôtô cũng đi t A đn B v i v n t c 60km/h . H i hai ng i g p nhau lúc m y gi .ộ ừ ế ớ ậ ố ỏ ườ ặ ấ ờ
Bài 6. M t ng i đi xe máy kh i hành t A lúc 6 gi sáng và đi đn B . Sau khi đi đc 2/3 quãng ộ ườ ở ừ ờ ế ượ
đng v i v n t c 50km/h thì ng i đo ngh 30phút r i ti p t c đi quãng đng còn l i v i v n ườ ớ ậ ố ườ ỉ ồ ế ụ ườ ạ ớ ậ
t c 40km/h và đn B lúc 13gi cùng ngày .Tính quãng đng AB .ố ế ờ ườ
Bài 7. M t đi th m theo k ho ch m i ngày ph i khai thác 50mộ ộ ợ ỏ ế ạ ỗ ả 3 than , nh ng khi th c hi nư ự ệ
do c i ti n k thu t nên m i ngày đi khác thác đc 57 mả ế ỹ ậ ỗ ộ ượ 3 , vì v y không nh ng đi đã hoàn ậ ữ ộ
thành s m h n k ho ch 1 ngày mà còn làm thêm đc 13mớ ơ ế ạ ượ 3 than . H i theo k ho ch đi ỏ ế ạ ộ
ph i khai thác bao nhiêu mả3 than?
Bài 8. Trong tháng đu hai t công nhân s n xu t đc 800 chi ti t máy. Tháng th hai, t I ầ ổ ả ấ ượ ế ứ ổ
v t m c 15%, t II v t m c 20%, do đó c hai t s n xu t đc 945 chi ti t máy. Tính xemượ ứ ổ ượ ứ ả ổ ả ấ ượ ế
trong tháng đu m i t đã s n xu t đc bao nhiêu chi ti t máy.ầ ỗ ổ ả ấ ượ ế
Bài 9: M t s t nhiên có hai ch s , ch s hàng ch c g p 3 l n ch s hàng đn v . N u ộ ố ự ữ ố ữ ố ụ ấ ầ ữ ố ơ ị ế
đi ch hai ch s đó cho nhau thì đc m t s nh h n s ban đu 18 đn v . Tìm s đó.ổ ỗ ữ ố ượ ộ ố ỏ ơ ố ầ ơ ị ố
Bài 10. M t vòi n c ch y vào b không có n c , cùng lúc đó m t vòi khác ch y t b ra . M i ộ ướ ả ể ướ ộ ả ừ ể ỗ
gi l ng n c ch y ra b ng 4/5 l ng n c ch y vào . Sau 5 gi l ng n c trong b đt 1/8 ờ ượ ướ ả ằ ượ ướ ả ờ ượ ướ ể ạ
dung tích c a b . H i n u ch m vòi n c ch y vào thì sau bao lâu s đy b ?ủ ể ỏ ế ỉ ở ướ ả ẽ ầ ể
Bài 11:Chú An đi xe máy đi làm, m c xăng tiêu th trong tháng 1 là 15 lít xăng, tháng 2 là 20 lít ứ ụ
xăng, c hai tháng mua h t 740.000 đng ti n xăng. Bi t giá xăng tháng 2 tăng h n tháng 1 là ả ế ồ ề ế ơ
2.000 đng. Tính giá m t lít xăng tháng 1?ồ ộ
Bài 12: M t hình ch nh t có chu vi 372m n u tăng chi u dài 21m và tăng chi u r ng 10m thìộ ữ ậ ế ề ề ộ
di n tích tăng 2862mệ2. Tính kích th c c a hình ch nh t lúc đu?ướ ủ ữ ậ ầ
Bài t p bi n đi bi u th c h u tậ ế ổ ể ứ ữ ỉ
Bài 13: Cho hai bi u th c:ể ứ A =
và B =
2
1 2 1x x
x x x
− +
++
a) Tính giá tr c a bi u th c A khi x = ị ủ ể ứ
2
3
−
b) Rút g n Bọ
c) Tìm s d ng x đ ố ươ ể
3
2
A
B>
Bài 14: Cho bi u th cể ứ :
2
2 3 1
:
2 2 2 2 1 2
x x x
Cx x x x
− −
� �
= − +
� �
− + −
� �
a) Rút g n C.ọ
b) Tìm giá tr nguyên x đ C có giá tr nguyênị ể ị
c) Tìm x đ C<0ể
Bài 15: Cho bi u th cể ứ :
( )
2 2
2
2
3 1 12 1
4 2 2 2
x x
Dx x x x
� �
� � +
= − −�
� �
� �
� �
− − + +
� �
� �
+
a) Rút g n D.ọ
b) Tìm giá tr nguyên d ng c a x đ D có giá tr nguyênị ươ ủ ể ị
c) Tìm x đ D = ể
2
5
−
d) Tìm x đ D > 0.ể
Bài t p nâng caoậ
Bài 16: Ch ng minh b t đng th c :ứ ấ ẳ ứ
a)
c
a
a
b
b
c
a
c
c
b
b
a
2
2
2
2
2
2
b)
8))()(( bc
a
c
ba
c
b
ac
b
a
v í a ,b , c > 0ớ
c)
( )
1 1 4A a b a b
� �
= + +
� �
� �
( v i a.b > 0)ớd)
6;( , , 0)
a b b c c a
B a b c
c a b
+ + +
= + + >
e) Cho 2 s a, b tho mãn: a + b = 1. Ch ng minh: aố ả ứ 3 + b3 +ab
2
1
f) Cho a, b, c là các s d ng. ố ươ Ch ng minh r ng: ứ ằ
2
222 cba
ba
c
ac
b
cb
a
Bài 17 : Xét ph ng trình ( m-1) x – m +5 = 0 ( n x ) ươ ẩ
a) Tìm m đ ph ng trình nh n x = -3 là nghi m.ể ươ ậ ệ
b) Ch ng t v i m = 1 ph ng trình vô nghi m.ứ ỏ ớ ươ ệ
c*) Gi i và bi n lu n ph ng trình.ả ệ ậ ươ
Bài 18*. Cho b t ph ng trình ( mấ ươ 2 + 1) x – m -2 > 0
Tìm m đ m i x > 2 là nghi m c a b t ph ng trình.ể ọ ệ ủ ấ ươ
II. HÌNH H C.Ọ
Bài 1 : Cho ABC , đng trung truy n AM . Đng phân giác c a góc AMB c t c nh ABườ ế ườ ủ ắ ạ
D , đng phân giác c a góc AMC c t c nh AC E . Bi t BC = 6 cm và AM = 4cm . G i ở ườ ủ ắ ạ ở ế ọ
N là giao đi m c a AM v i DEể ủ ớ
a) Tính các t s ỉ ố
DA
BD
và
EA
CE
b) C/m : DE // BC c) C/m: N là trung đi m c a DE ể ủ
Bài 2. Cho tam giác ABC cân A, phân giác c a góc B và góc C c t AC và AB D và E.ở ủ ắ ở
a) Ch ng minh DE //BC. b) DE = 10 cm, BC = 16 cm. Tính AB?ứ
Bài 3 Cho hình thang ABCD ( AB //CD) c a AB = 7cm, CD = 12cm. G i M là trung đi m CD, E làủ ọ ể
giao đi m MA và BD, F là giao đi m MB và AC.ể ể
a) Ch ng minh EF //AB b) Tính EF?ứ
Bài 4 : Cho hình thang ABCD( AB// CD) , AB = 4cm , BD = 6cm , CD = 9cm và góc ADB = 400
G i I là giao đi m c a AC và BD ọ ể ủ
a) cm : IA. ID = IB . IC b) Cm : ABD đng d ng v i ồ ạ ớ BDC . Tìm t s đng d ng k .ỉ ố ồ ạ
c) Tính s đo ố
B
ˆ
c a hình thang ABCDủ
Bài 5 : Cho ABC có AB = 2cm , AC = 2,5 cm và BC = 3 cm . Trên tia đi c a tia AB l y ố ủ ấ
đi m D sao cho AD = AC. ể
a) c/m: ABC đng d ng v i ồ ạ ớ CBD . Tìm t s đng d ng k. b) Tính đ dài đo n CDỉ ố ồ ạ ộ ạ
c) c/m: góc BAC = 2 góc ACB
Bài 6: Cho tam giác ABC vuông A ,có AB = 6cm; AC = 8cm. V đng cao AH và phânở ẽ ườ
giác BD. Ch ng minh:ứ
a) ΔABH ~ ΔCAH
b) Tính đ dài AD, DC?ộ
c) G i I là giao đi m c a AH và BD, ch ng minh AB.BI = BD.HB, suy ra ΔAID cân.ọ ể ủ ứ
AC
B
A'
B'
C'
d) K đng th ng qua A vuông góc v i BD t i M c t BC t i N. Tính t s di n tích ΔAID vàẻ ườ ẳ ớ ạ ắ ạ ỉ ố ệ
ΔBAN.
Bài 7 : Cho xÂy nh n , trên tia Ax l y E và C sao cho AE = 2cm , AC = 9 cm Trên tia Ay l y Dọ ấ ấ
và B sao cho AD = 3cm , AB = 6cm
a) Cm : ABC đng d ng v i ồ ạ ớ AED . Tìm t s đng d ng .ỉ ố ồ ạ
b) K DF // BC (F ẻ AC). Cm ADF đng d ng v i ồ ạ ớ AED . Tính t s ỉ ố
AED
ADF
S
S
c) Tìm đi u ki n c a ề ệ ủ ABC đ : AEể2 + DE2 = AF. AE
Bài 8 : Cho hình ch nh t ABCD , E là trung đi m c a AB.Bi t AB = 36cm AD = 24 cm . Tia ữ ậ ể ủ ế
DE l n l t c t AC và đng th ng BC t i F và G ầ ượ ắ ườ ẳ ạ
a) Tính đ dài các đo n DE , DG b) Tính đ dài đo n th ng DF và FE ộ ạ ộ ạ ẳ
c) Cm : FD 2 = FE. FG ( không dùng đ dài c nh )ộ ạ
d) Cm : Tích AE. CG không đi khi đi m E thay đi v trí trên AB ổ ể ổ ị
Bài 9 : Cho ABC cân t i A , M là trung đi m c a BC . Trên AB và AC l n l t l y các đi mạ ể ủ ầ ượ ấ ể
D và E sao cho CME = BDM
a) Cm : BDM đng d ng v i ồ ạ ớ CME. b) Cm : BD. CE = BM2
c) Cm : BDM đng d ng v i ồ ạ ớ MDE d) Cm : DM là tia phân giác c a góc BDE ủ
Bài 10: Cho ΔABC, các đng cao AD, BE, CF c t nhau t i H.ườ ắ ạ
a) Ch ng minh: AE.AC = AF. AB.ứ
b) Ch ng minh: ΔAEF ~ ΔABC.ứ
c) Ch ng minh: ΔFHE ~ ΔBHC.ứ
d) TRên đng th ng BD, CF l y các đi m M, N sao cho các góc AMC và góc ANB là gócườ ẳ ấ ể
vuông. Ch ng minh: ΔAMN cân.ứ
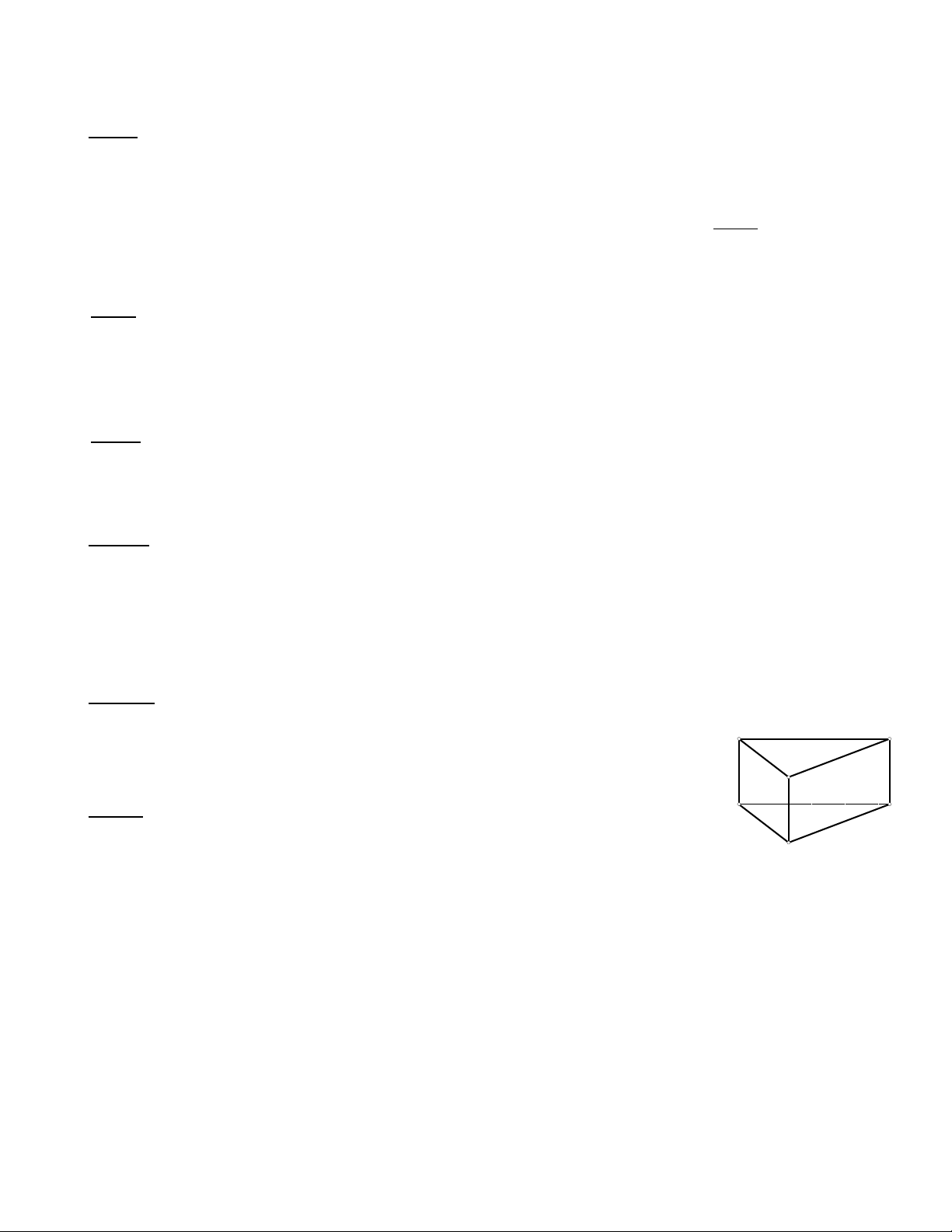
Bài 11. Hình lăng tr đng ABC.A’B’C’ có hai đáy ABC và A’B’C’ là các tam giác vuông t iụ ứ ạ
A và A’ (hình ).
Tính Sxq và th tích c a hình lăng tr . ể ủ ụ
Bi t: AB = 9cm, BC = 15cm, AA’ = 10cm. ế
Bài 12: Cho hình chóp tam giác đu S. ABC có AB = 8cm, chi u cao ề ề
c a chóp là 5cmủ
a) Tính bán kính đng tròn đi qua các đnh c a m t đáy.ườ ỉ ủ ặ
b) Tính kho ng cách t S đn các đnh A, B , Cả ừ ế ỉ