
TRƯỜNG THPT HAI BÀ TRƯNG ĐỀ CƯƠNG ÔN TẬP HKII NĂM HỌC 2018 - 2019
TỔ TOÁN MÔN TOÁN – KHỐI 11
H và tên: ……………………...………….……; Tr ng:…………….…………………; L p:ọ ườ ớ
……………..
A. N i dungộ
I. Gi i tích: ảT §1 ch ng IV. Gi i h n đn §5 ch ng V. Đo hàm.ừ ươ ớ ạ ế ươ ạ
II. Hình h c:ọ T §1 đn §5 ch ng III. Vect trong không gian. Quan h vuông góc.ừ ế ươ ơ ệ
B. M t s bài t p tham kh oộ ố ậ ả
Xem l i các bài t p trong SGK và SBT Đi s & Gi i tích, Hình h c 11 c b n.ạ ậ ạ ố ả ọ ơ ả
CHỦ ĐỀ I. GIỚI HẠN
Câu 1. Dãy s nào sau đây có gi i h n b ng ố ớ ạ ằ
0
?
A.
2
3
−
=
n
n
u
.B.
6
5
=
n
n
u
.C.
3
3
1
−
=+
n
n n
un
.D.
2
4= −
n
u n n
.
Câu 2. Phát bi u nào trong các phát bi u sau là ể ể sai?
A.
lim 0
n
q=
( )
| | 1q>
.B.
lim c c
=
.C.
1
lim 0
k
n=
( )
1k>
.D.
1
lim 0
n=
.
Câu 3. Tính gi i h n ớ ạ
3
2
2
lim .
3 2
n n
n n
−
+ −
A.
.−
B.
1.
3
C.
.+
D.
0.
Câu 4. Cho
2 3 2
3
5 1
lim 4
a n n n b
n bn a
+ − + =
− +
. Có bao nhiêu giá tr ị
a
nguyên d ng đ ươ ể
[ ]
0; 4b
?
A.
0
.B.
4
.C.
16
.D.
2
.
Câu 5. Có bao nhiêu giá tr nguyên c a tham s ị ủ ố
a
thu c ộ
( )
10;10
−
đ ể
( )
2 3
lim 5 3 2n a n
− − = −
?
A.
19
.B.
3
.C.
5
.D.
10
.
Câu 6. Tính gi i h n ớ ạ
2 3
3 2
7 2 1
lim .
3 2 1
n n
In n
− +
=+ +
A.
7
3
.B.
2
3
−
.C.
0
.D.
1
.
Câu 7. Bi t ế
3 2
3
2 4 1
lim 2 2
n n
an
+ − =
+
v i ớ
a
là tham s . Tính ố
2
a a
−
.
A.
12
−
.B.
2
−
. C.
0
.D.
6−
.
Câu 8. Cho hai s th cố ự
;a b
th a mãn ỏ
2
3 2 3
5 3
lim 1
5 4 2
an n
n n bn
− + = −
− + +
. Tính
S a b
= −
.
A.
5S
=
.B.
3S
= −
.C.
3S=
.D.
5S
= −
.
Câu 9. Cho dãy s ố
( )
n
u
v i ớ
( ) ( )
1 1 1
...
1.3 3.5 2 1 2 1
n
un n
= + + + − +
. Tính
lim
n
u
.
A.
0
.B.
1
2
.C.
1
4
.D.
1
.
Câu 10. Có bao nhiêu giá tr nguyên l n h n ị ớ ơ
10
−
c a tham s ủ ố
m
đ ể
()
2
lim 4 3 5n mn
+ − − = +
?
A.
9
.B.
10
.C.
11
.D.
12
.
Câu 11. Có bao nhiêu giá tr nguyên c a tham s ị ủ ố
a
thu c kho ng ộ ả
( )
0;2018
đ có ể
1
9 3 1
lim 5 9 2187
n n
n n a
+
+
+
+
?
A.
2011
.B.
2016
.C.
2019
.D.
2009
.
Tr ng THPT Hai Bà Tr ng – Huườ ư ế Trang 1/14

Câu 12. Tính gi i h n ớ ạ
2 2 2
1 1 1
lim 1 1 ... 1
2 3 n
− − −
.
A. 1. B.
1
2
.C.
1
4
.D.
3
2
.
Câu 13. Tính t ngổ t t c các giá tr th c c a tham s ấ ả ị ự ủ ố
a
đ ể
( )
()
2 2 2
lim 2 1 2n a n n a n
+ − + + + =
.
A.
1
−
. B.
5−
C.
1
. D.
5
.
Câu 14. Tính t ng ổ
1
1 1 1 1
1 ... ...
3 9 27 3
n
S
−
= − + − + + − +
v i ớ
*
n
ᆬ
.
A.
1S
=
.B.
3
4
S
=
.C.
S
= +
.D.
3
2
S
=
.
Câu 15. Gi s ta có ả ử
( )
lim
x
f x a
+
=
và
( )
lim
x
g x b
+
=
. Trong các m nh đ sau, m nh đ nào ệ ề ệ ề sai?
A.
( ) ( )
lim
x
f x g x ab
+
=
.B.
( ) ( )
lim
x
f x g x a b
+
− = −
.
C.
( )
( )
lim
x
f x a
g x b
+
=
. D.
( ) ( )
lim
x
f x g x a b
+
+ = +
.
Câu 16. Cho các gi i h n ớ ạ
( )
0
lim 2
x x
f x
=
;
( )
0
lim 3
x x
g x
=
. Tính gi i h n ớ ạ
( ) ( )
0
lim 3 4
x x
f x g x
−
.
A.
5
. B.
2
.C.
6
−
.D.
3
.
Câu 17. Tính gi i h n ớ ạ
2 3
lim 1 3
x
x
x
+
−
−
.
A.
2
3
.B.
2
3
−
.C.
3
2
−
.D.
3
−
.
Câu 18. Cho
()
2
lim 5 5
x
x ax x
−
+ + + =
thì
a
là
1
nghi m c a ph ng trình nào trong các ph ng trìnhệ ủ ươ ươ
sau?
A.
2
11 10 0x x
− + =
. B.
2
5 6 0x x
− + =
.C.
2
8 15 0x x
− + =
.D.
2
9 10 0x x
+ − =
.
Câu 19. Tính gi i h n ớ ạ
()
2
lim 4 1
x
I x x x
−
= + + +
.
A.
2I= −
.B.
4I= −
.C.
1I=
.D.
1I= −
.
Câu 20. Cho
( )
1
10
lim 5
1
x
f x
x
−=
−
. Tính gi i h n ớ ạ
( )
( )
( )
( )
1
10
lim
1 4 9 3
x
f x
x f x
−
− + +
.
A.
1
.B.
2
.C.
10
.D.
5
3
.
Câu 21. Tính gi i h nớ ạ
( )
3 2
lim 3 5 9 2 2017
x
x x x
−
+ − −
.
A.
−
.B.
3
.C.
3
−
.D.
+
.
Câu 22. Cho hai s th c ố ự
a
và
b
tho mãn ả
2
4 3 1
lim 0
2 1
x
x x ax b
x
+
− + − − =
+
. Tính
2a b+
.
A.
4−
.B.
5−
.C.
4
.D.
3−
.
Câu 23. Tính gi i h n ớ ạ
2
3 2
lim 2
x
x
x
−
+
+
.
A.
−
.B.
2
.C.
+
.D.
3
2
.
Câu 24. Bi t ế
2 2
2
1 1
lim 3 4 4 12 20
x
x x x x
+
− − − +
là m t phân s t i gi n ộ ố ố ả
( )
0 .
ab
b
>
Tính
2
6S a b
= −
.
A.
10S
= −
.B.
10S
=
.C.
32S
=
.D.
21S
=
.
Câu 25. Bi t ế
( )
()
2
lim 4 3 1 0
x
x x ax b
+
− + − + =
. Tính
4a b
−
.
Tr ng THPT Hai Bà Tr ng – Huườ ư ế Trang 2/14
A.
3
.B.
5
.C.
1−
.D.
2
.
Câu 26. Tính gi i h n ớ ạ
2 2
4 1
lim 2 3
x
x x x
x
−
− − +
+
.
A.
1
2
−
.B.
+
.C.
−
.D.
1
2
.
Câu 27. Cho
2
1 2017 1
lim 2018 2
x
a x
x
−
+ + =
+
;
()
2
lim 1 2
x
x bx x
+
+ + − =
. Tính
4P a b= +
.
A.
3P=
. B.
1P= −
.C.
2P=
.D.
1P=
.
Câu 28. Giá tr c a s th c ị ủ ố ự
m
sao cho
( )
( )
2
3
2 1 3
lim 6
4 7
x
x mx
x x
+
− + =
+ +
là
A.
3m
= −
.B.
3m
=
.C.
2m
=
.D.
2m
= −
.
Câu 29. Cho hàm s ố
( )
y f x
=
xác đnh trên ị
{ }
\ 1
ᆬ
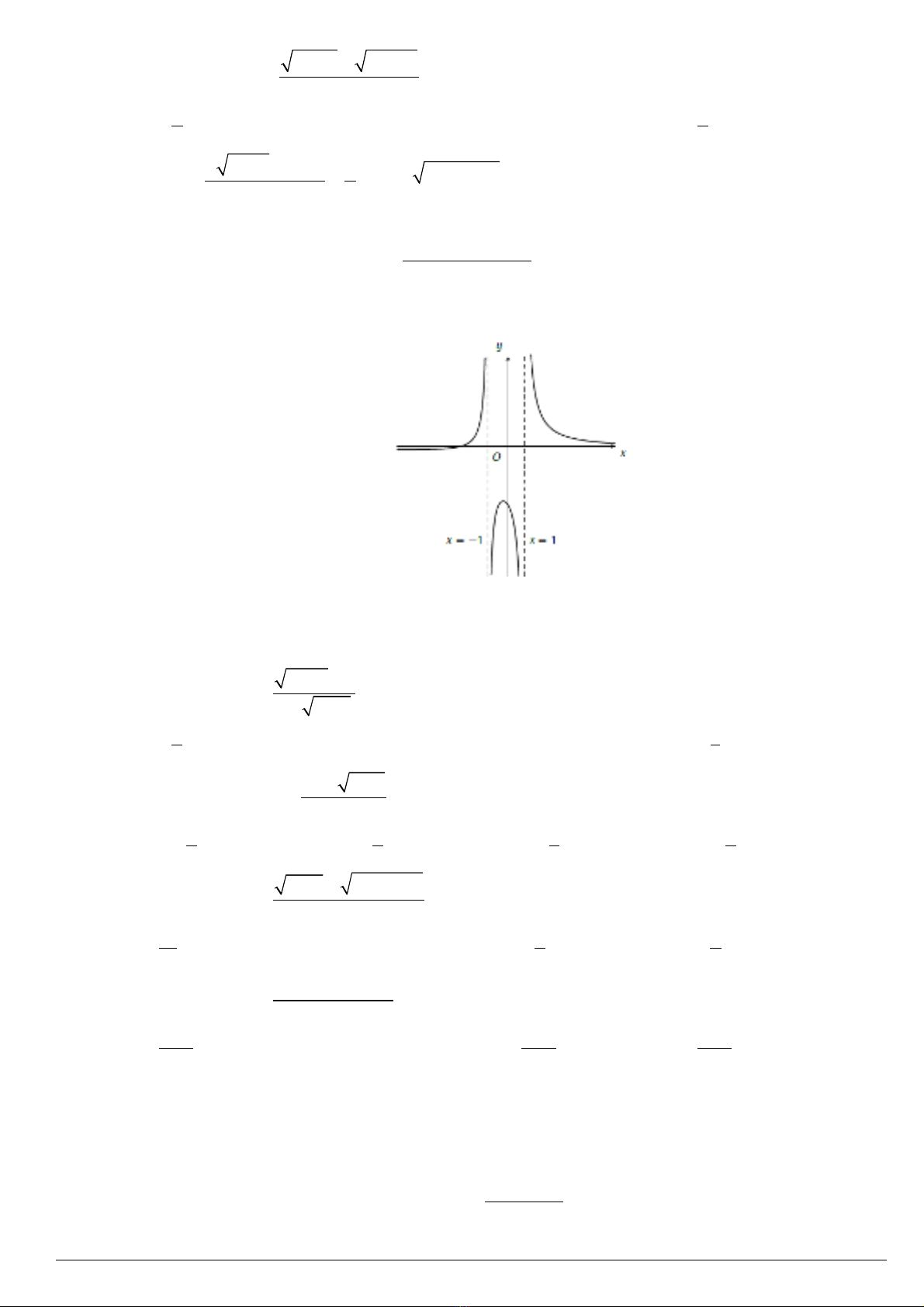
có đ th nh hình v . Kh ng đnh nào ồ ị ư ẽ ẳ ị đúng?
A.
( )
( )
( )
11
lim ; lim
xx
f x f x
+ +
−
= + = +
.B.
( )
( )
( )
11
lim ; lim
xx
f x f x
+ +
−
= + = −
.
C.
( )
( )
( )
11
lim ; lim
xx
f x f x
− −
−
= + = +
.D.
( )
( )
( )
11
lim ; lim
xx
f x f x
− −
−
= − = −
.
Câu 30. Tính gi iớ h n ạ
5
3 1 4
lim 3 4
x
x
x
+ −
− +
.
A.
9
4
−
.B.
3
−
.C.
18
−
.D.
3
8
−
.
Câu 31. Tính gi i h n ớ ạ
2
1
2 3
lim 1
x
x x
Ix
− +
=−
.
A.
7.
8
I=
B.
3.
2
I=
C.
3.
8
I=
D.
3.
4
I=
Câu 32. Tính gi i h n ớ ạ
2
3
1
7 2
lim 1
x
x x x
x
+ − + +
−
.
A.
1
12
B.
+
C.
3
2
−
D.
2
3
−
.
Câu 33. Tính gi i h n ớ ạ
( )
2
3 3
1
lim
x a
x a x a
x a
− + +
−
.
A.
2
1
3
a
a
−
.B.
+
.C.
2
1
3
a
a
+
.D.
1
3
a
a
−
.
Câu 34. Cho hàm số
( )
y f x=
liên t c trênụ
( )
;a b
. Đi u ki n c n và đ đ hàm s liên t c trên ề ệ ầ ủ ể ố ụ
[ ]
;a b
là
A.
( ) ( )
lim
x a
f x f a
+
=
và
( ) ( )
lim
x b
f x f b
+
=
.B.
( ) ( )
lim
x a
f x f a
−
=
và
( ) ( )
lim
x b
f x f b
−
=
.
C.
( ) ( )
lim
x a
f x f a
+
=
và
( ) ( )
lim
x b
f x f b
−
=
.D.
( ) ( )
lim
x a
f x f a
−
=
và
( ) ( )
lim
x b
f x f b
+
=
.
Câu 35. Tìm tham s th c ố ự
m
đ hàm s ể ố
( )
y f x=
2
12 khi 4
4
1 khi 4
x x x
x
mx x
+ − −
=+
+ = −
liên t c t i đi m ụ ạ ể
0
4x= −
.
Tr ng THPT Hai Bà Tr ng – Huườ ư ế Trang 3/14

A.
4m
=
.B.
3m
=
.C.
2m
=
.D.
5m
=
.
Câu 36. Có t t c bao nhiêu giá tr c a ấ ả ị ủ
a
đ hàm s ể ố
2
2
( 2) 2 khi 1
( ) 3 2
8 khi 1
ax a x x
f x x
a x
− − −
=+ −
+ =
liên t c t iụ ạ
1x
=
?
A.
1
.B.
0
. C.
3
. D.
2
.
Câu 37. Hàm s nào trong các hàm s d i đây ố ố ướ không liên t c trên ụ
?ᆬ
A.
y x=
.B.
1
x
yx
=+
.C.
siny x=
.D.
2
2 1
1
x
yx
−
=+
.
Câu 38. Cho hàm s ố
( ) ( )
2khi 1
2
3 khi 1
mx n x
f x
mnx x
+
=+ <
liên t c trên ụ
ᆬ
. Tính
2 2
+
m n
.
A.
1
.B.
2
.C.
3
.D.
4
.
Câu 39. G i ọ
a
,
b
là hai s th c đ hàm s ố ự ể ố
( )
2
khi 1
1
2 1 khi 1
x ax b x
f x x
ax x
+ +
=−
− =
liên t c trên ụ
ᆬ
. Tính
a b−
.
A.
0
.B.
1−
.C.
5−
.D.
7
.
Câu 40. Cho hàm s ố
( )
f x
xác đnh trên ị
[ ]
;a b
. Tìm m nh đ ệ ề đúng.
A. N u hàm s ế ố
( )
f x
liên t c trên ụ
[ ]
;a b
và
( ) ( )
0f a f b >
thì ph ng trình ươ
( )
0f x =
không có
nghi m trong kho ng ệ ả
( )
;a b
.
B. N u ế
( ) ( )
0f a f b <
thì ph ng trình ươ
( )
0f x =
có ít nh t m t nghi m trong kho ng ấ ộ ệ ả
( )
;a b
.
C. N u hàm s ế ố
( )
f x
liên t c, tăng trên ụ
[ ]
;a b
và
( ) ( )
0f a f b >
thì ph ng trình ươ
( )
0f x =
không
có nghi m trong kho ng ệ ả
( )
;a b
.
D. N u ph ng trình ế ươ
( )
0f x =
có nghi m trong kho ng ệ ả
( )
;a b
thì hàm s ố
( )
f x
liên t c trênụ
( )
;a b
.
Câu 41. Ph ng trình nào d i đây có nghi m trong kho ng ươ ướ ệ ả
( )
0;1
A.
2
2 3 4 0x x
− + =
.B.
( )
57
1 2 0x x
− − − =
.C.
4 2
3 4 5 0x x
− + =
.D.
2017
3 8 4 0x x
− + =
.
Câu 42. Cho ph ng trình ươ
( )
4 2
2 5 1 0 1x x x− + + =
. Kh ng đnh nào sau đây là ẳ ị đúng?
A.
( )
1
có nghi m trong kho ng ệ ả
( )
1;1
−
.B.
( )
1
ch có m t nghi m trong kho ng ỉ ộ ệ ả
( )
2;1
−
.
C.
( )
1
có ít nh t m t nghi m trong ấ ộ ệ
( )
0; 2
.D.
( )
1
không có nghi m trong kho ng ệ ả
( )
2; 0
−
.
Câu 43. Cho ph ng trình ươ
( )
( )
( )
( )
2 2 3
3 1 4 3 0 1m x x x
+ − − − + =
, v i ớ
m
là tham s . Kh ng đnh nào sauố ẳ ị
đây v ph ng trình ề ươ
( )
1
là kh ng đnh ẳ ị đúng?
A.
( )
1
có đúng
4
nghi m phân bi tệ ệ .B.
( )
1
vô nghi mệ.
C.
( )
1
có ít nh t ấ
2
nghi m phân bi tệ ệ .D.
( )
1
có đúng m t nghi mộ ệ .
Câu 44. Tìm t t c các giá tr th c c a ấ ả ị ự ủ
m
đ ph ng trình ể ươ
( )
( )
2020
2019
1 2 2 3 0m x x x− − + − =
vô nghi m.ệ
A.
1m
=
B.
m
∀
ᆬ
C.
0m
=
D. Không có giá tr ị
m
------------------------
. CHỦ ĐỀ 2. ĐẠO HÀM
Câu 45. Cho
3
1y x= +
. G i ọ
x∆
là s gia c a đi s t i ố ủ ố ố ạ
x
và
y
∆
là s gia t ng ng c a hàm s , tínhố ươ ứ ủ ố
y
x
∆
∆
.
A.
2 3
3 3 .x x x x− ∆ + ∆
.B.
2 2
3 3 .x x x x+ ∆ + ∆
.C.
2 2
3 3 .x x x x+ ∆ − ∆
.D.
2 3
3 3 .x x x x+ ∆ + ∆
.
Câu 46. S gia ố
y
∆
c a hàm s ủ ố
2
2 5y x x= + −
t i đi m ạ ể
0
1x=
là
Tr ng THPT Hai Bà Tr ng – Huườ ư ế Trang 4/14

A.
( )
2
2 5
x x
∆ + ∆ −
. B.
( )
2
2
x x
∆ − ∆
.C.
( )
2
4
x x
∆ − ∆
.D.
( )
2
4
x x
∆ + ∆
.
Câu 47. Cho hàm s ố
( )
y f x=
có đo hàm th a mãn ạ ỏ
( )
6 2.f
=
Giá tr c a bi u th c ị ủ ể ứ
( ) ( )
6
6
lim 6
x
f x f
x
−
−
b ngằ
A.
12.
B.
2
.C.
1.
3
D.
1.
2
Câu 48. Cho hàm s ố
( )
2
1, 1
2 , 1.
x x
y f x x x
+
= = <
M nh đ ệ ề sai là
A.
( )
1 2f=
.B.
( )
1f∃
.C.
( )
0 2.f=
D.
( )
2 4.f=
Câu 49. Cho hàm s ố
( )
2
1 khi 0
1 khi 0
ax bx x
f x ax b x
+ +
=− − <
. Bi t ế
( )
f x
có đo hàm t i ạ ạ
0x=
. Tính
2T a b= +
.
A.
4T= −
.B.
0T=
.C.
6T= −
.D.
4T=
.
Câu 50. Đo hàm c a hàm s ạ ủ ố
5 3 2
2 4y x x x= − −
là
A.
4 2
10 3 2y x x x
= − −
.B.
4 2
5 12 2y x x x
= − −
.C.
4 2
10 12 2y x x x
= + −
.D.
4 2
10 12 2y x x x
= − −
.
Câu 51. Cho hàm s ố
( )
2 1
1
x
f x x
−
=+
xác đnh trên ị
{ }
\ 1ᆬ
. Đo hàm c a hàm s ạ ủ ố
( )
f x
là
A.
( ) ( )
2
1
1
f x
x
=+
.B.
( ) ( )
2
2
1
f x
x
=+
.C.
( ) ( )
2
1
1
f x
x
−
=+
.D.
( ) ( )
2
3
1
f x
x
=+
.
Câu 52. Tính đo hàm c a hàm s ạ ủ ố
2
2
2 2 3
3
x x
yx x
+ +
=+ +
.
A.
2
3
23x x
−+ +
.B.
( )
2
2
6 3
3
x
x x
+
+ +
.C.
( )
2
2
3
3x x+ +
.D.
2
3
3
x
x x
+
+ +
.
Câu 53. Cho hàm s ố
( ) ( ) ( ) ( ) ( )
1 2 3 4f x x x x x x
= − − − −
. Tính
( )
0f
.
A.
42
.B.
24
.C.
24
−
.D.
0
.
Câu 54. Cho
( )
2 2
2
2 3 5
33
x x ax bx c
xx
− + − +
=
−−
. Tính
S a b c
= + +
.
A.
0S
=
.B.
12S
=
.C.
6S
= −
.D.
18S
=
.
Câu 55. Bi t ế
( )
3 2
4 1 4 1 4 1
x ax b
x x x
− −
=
− − −
. Tính
a
Eb
=
.
A.
1E
= −
.B.
4E
= −
.C.
2E
= −
.D.
4E
=
.
Câu 56. Tính đo hàm c a hàm s ạ ủ ố
( )
2
2 1y x x= − +
.
A.
2
2
2 2 1
1
x x
y
x
− −
=+
.B.
2
2
2 2 1
1
x x
y
x
+ +
=+
.C.
2
2
2 2 1
1
x x
y
x
− +
=−
.D.
2
2
2 2 1
1
x x
y
x
− +
=+
.
Câu 57. Hàm s nào sau đây không có đo hàm trên ố ạ
ᆬ
?
A.
1y x
= −
.B.
2
4 5y x x= − +
.C.
siny x
=
.D.
2 cosy x
= −
.
Câu 58. Tính đo hàm c a hàm s ạ ủ ố
( )
3
21y x x= − +
t i đi m ạ ể
1x
= −
.
A.
27
.B.
27
−
.C.
81
.D.
81
−
.
Câu 59. Cho hàm s ố
( ) ( )
3 2
2 2
3
m
f x x m x x= − − + +
. Đ đo hàm ể ạ
( )
f x
b ng bình ph ng c a m t nhằ ươ ủ ộ ị
th c b c nh t thì giá tr ứ ậ ấ ị
m
là
A.
1−
ho c ặ
1
.B.
1
ho c ặ
4
.C.
4−
ho c ặ
4
.D. Không có giá tr nào.ị
Câu 60. Tìm t t c các giá tr c a tham s ấ ả ị ủ ố
m
đ hàm s ể ố
( )
3 2 3
1 2y x m x x m= − − + +
có
' 0,y x ∀ ᆬ
.
A.
1 2 6; 1 2 6
− − − +
.B.
1 2 6;1 2 6
− +
.C.
1 6; 1 6
− − − +
.D.
1 6;1 6
− +
.
Tr ng THPT Hai Bà Tr ng – Huườ ư ế Trang 5/14



![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










![Phiếu bài tập cuối tuần Tiếng Việt 1 tuần 2 đề 2: [Hướng dẫn chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250728/thanhha01/135x160/42951755577464.jpg)

