1
TRƯỜNG THPT YÊN HÒA
BỘ MÔN: TOÁN
ĐỀ CƯƠNG ÔN TẬP HỌC KỲ I
NĂM HỌC 2023 - 2024
MÔN: TOÁN - KHỐI 12
CẤU TRÚC
PHẦN TT
NỘI DUNG CÁC DẠNG TOÁN Trang
GIẢI
TÍCH
1
SỰ BIẾN THIÊN VÀ
ĐỒ THỊ CỦA HÀM SỐ
Câu hỏi TN: 125 câu
Sự Đồng Biến, Nghịch Biến Của Hàm Số 2
Cực trị của hàm số 6
Giá trị lớn nhất – Giá trị nhỏ nhất 11
Đường tiệm cận của đồ thị hàm số 16
Đồ thị hàm số và các bài toán khác 18
2
HÀM SỐ LŨY THỪA –
HÀM SỐ MŨ – HÀM
SỐ LOGARIT
Câu hỏi TN: 100 câu
Lũy thừa với số mũ thực 27
Logarit 28
Hàm Số Lũy Thừa – Hàm Số Mũ – Hàm Số
Logarit 31
Phương trình mũ 37
Phương trình Logarit 38
HÌNH
HỌC
3
KHỐI ĐA DIỆN – THỂ
TÍCH KHỐI ĐA DIỆN
Câu hỏi TN: 50 câu
Khối đa diện 40
Thể tích khối chóp 41
Thể tích khối lăng trụ 43
Tỷ lệ thể tích các khối đa diện 45
Các bài toán thực tế 46
4
MẶT TRÒN XOAY –
KHỐI TRÒN XOAY
Câu hỏi TN: 60 câu
Mặt nón – Khối nón 48
Mặt trụ - Khối trụ 50
Mặt cầu – Khối cầu 52
2
A – PHẦN 1: GIẢI TÍCH
CHƯƠNG 1:
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
I - SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
1. Câu hỏi lý thuyết.
Câu 1. Cho hàm số
y f x
có đạo hàm trên
;
. Phát biểu nào sau đây là sai?
A. Hàm số
y f x
nghịch biến trên
;
a b
khi và chỉ khi
0, ;
f x x a b
và
0
f x
tại hữu
hạn giá trị
;
x a b
.
B. Hàm số
y f x
nghịch biến trên
;
khi và chỉ khi
1 2 1 2 1 2
, ; :
x x a b x x f x f x
.
C. Hàm số
y f x
nghịch biến trên khoảng
;
khi và chỉ khi
0, ;
f x x a b
.
D. Nếu
0, ;
f x x a b
thì hàm số
y f x
nghịch biến trên khoảng
;
.
Câu 2. Cho hàm số
y f x
có đạo hàm trên khoảng
;
a b
. Xét các mệnh đề sau:
I. Nếu hàm số
y f x
đồng biến trên khoảng
;
a b
thì
' 0, ;
f x x a b
.
II. Nếu
' 0, ;
f x x a b
thì hàm số
y f x
nghịch biến trên khoảng
;
a b
.
III. Nếu hàm
y f x
liên tục trên
;
a b
và
' 0, ;
f x x a b
thì hàm
y f x
đồng biến trên
;
a b
.
Số mệnh đề đúng trong 3 mệnh đề trên là
A.
3
. B.
0
. C.
2
. D.
1
.
2. Xét sự đồng biến, nghịch biến của hàm số khi biết đạo hàm của hàm số đó.
Câu 3. Hàm số
4
2 1
y x
đồng biến trên khoảng nào sau đây ?
A.
0;

. B.
1
;
2

. C.
1;
2

. D.
;0

.
Câu 4. Các khoảng nghịch biến của hàm số
4 2
2x 4
y x
là
A.
( 1;0)
và
(1; ).

B.
( ;1)

và
(1; ).

C.
( 1;0)
và
(0;1).
D.
( ; 1)

và
(0;1).
Câu 5. Cho hàm số
1
2
x
yx
. Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số đồng biến trên
.
B. Hàm số nghịch biến trên từng khoảng xác định.
C. Hàm số đồng biến trên
\{ 2}
.
D. Hàm số đồng biến trên từng khoảng xác định.
Câu 6. Cho hàm số
2
3
y x x
. Hàm số đồng biến trên khoảng nào sau đây?
A.
3
0;
2
. B.
0;3
. C.
3
;3
2
. D.
3
;
2

.
Câu 7. Cho hàm số
f x
có đạo hàm
2 3
1 1 2 .
f x x x x
Hàm số
f x
đồng biến trên khoảng nào,
trong các khoảng dưới đây?
A.
1;1
. B.
1;2
. C.
; 1

. D.
2;
3
Câu 8. Cho hàm số
y f x
xác định trên khoảng
0; 3
có tính chất
0, 0;3
f x x
và
0, 1;2
f x x
. Tìm khẳng định đúng trong các khẳng định sau:
A. Hàm số
f x
đồng biến trên khoảng
0;2
.
B. Hàm số
f x
không đổi trên khoảng
1;2
.
C. Hàm số
f x
đồng biến trên khoảng
1;3
.
D. Hàm số
f x
đồng biến trên khoảng
0;3
.
3. Xét sự đồng biến, nghịch biến của hàm số khi biết bảng biến thiên hoặc đồ thị của hàm số.
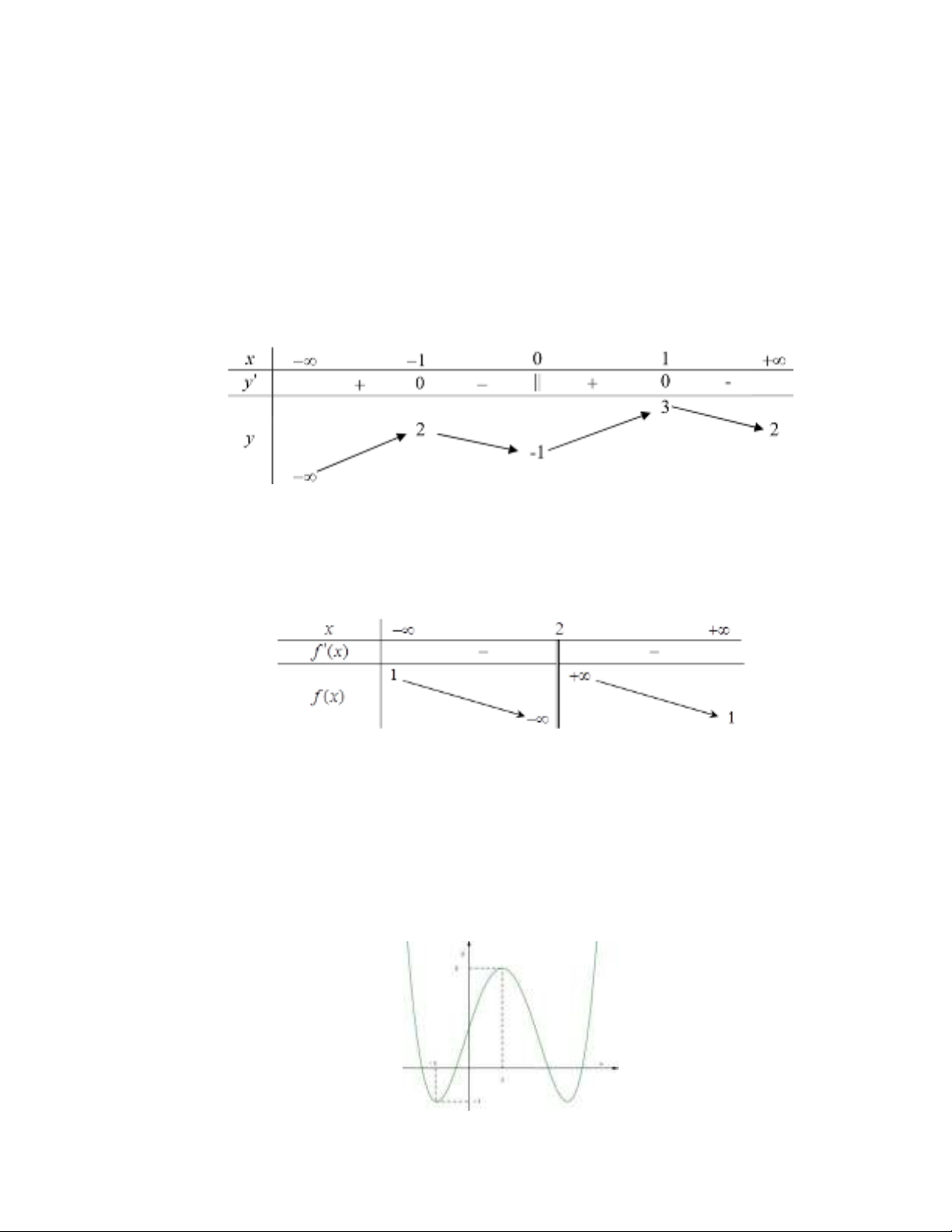
Câu 9. Cho hàm số
y f x
có bảng biến thiên như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
1;3
. B. Hàm số đồng biến trên khoảng
;2
.
C. Hàm số nghịch biến trên khoảng
2;1
. D. Hàm số nghịch biến trên khoảng
1;2
.
Câu 10. Cho hàm số
y f x
xác định trên
\ 2
và có bảng biến thiên như hình vẽ.
Mệnh đề nào sau đây là đúng?
A.
f x
nghịch biến trên từng khoảng
;2
và
2;
.
B.
f x
đồng biến trên từng khoảng
;2
và
2;
.
C.
f x
nghịch biến trên
.
D.
f x
đồng biến trên
.
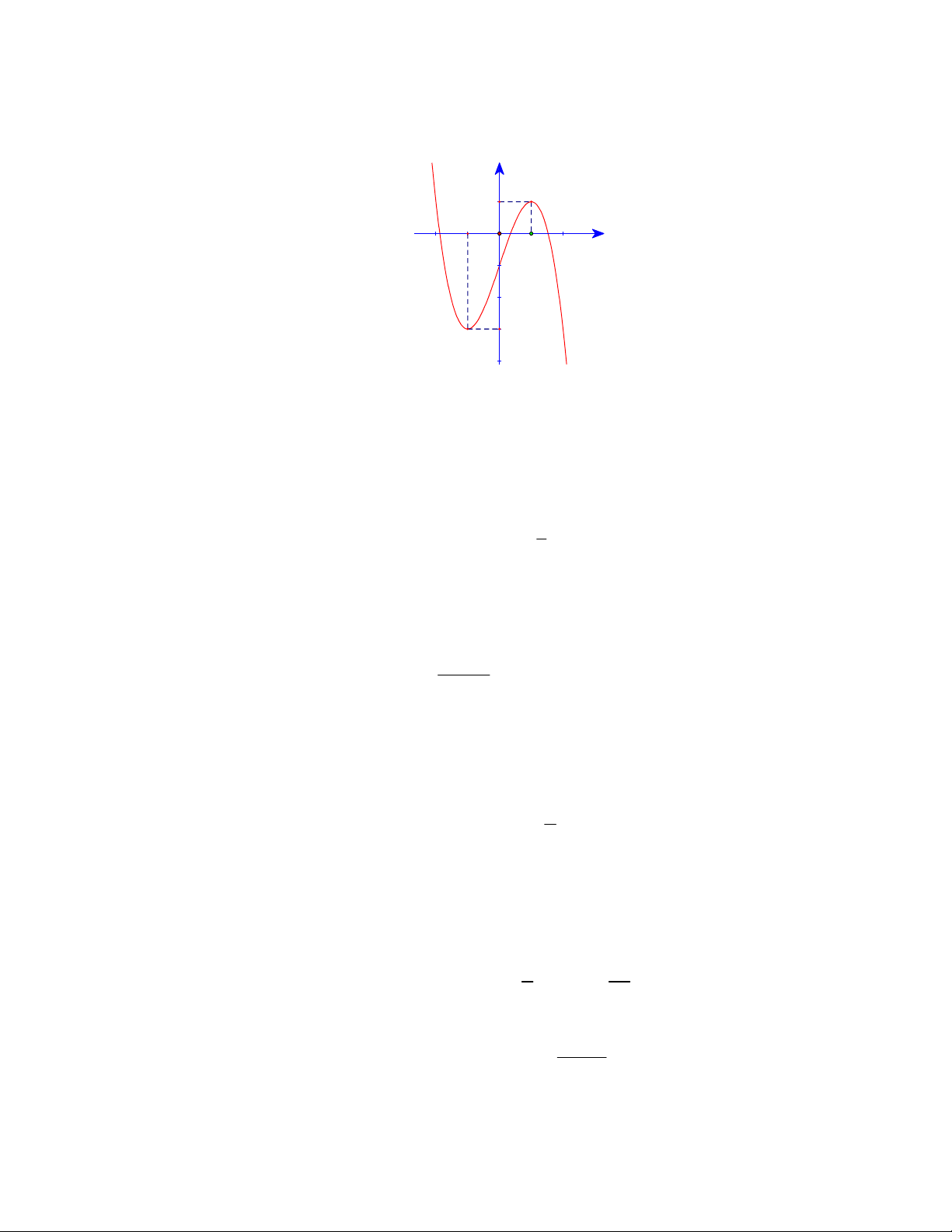
Câu 11. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào sau đây?
4
A.
;1

. B.
1;3
. C.
1;

. D.
0;1
.
Câu 12. Đường cong trong hình vẽ là đồ thị của một hàm số có dạng
3 2
0
y ax bx cx d a
. Hàm số đó
nghịch biến trên khoảng nào dưới đây?
A.
1;

. B.
;1

. C.
1;

. D.
1;1
.
4. Bài toán về sự đồng biến, nghịch biến của hàm số có chứa tham số.
Câu 13. Tìm
m
để hàm số
3
y x mx
nghịch biến trên
.
A.
0
m
. B.
0
m
. C.
0
m
. D.
0
m
.
Câu 14. Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
1
2 4 5
y x mx x
đồng biến trên
.
A.
1 1
m
. B.
1 1
m
. C.
0 1
m
. D.
0 1
m
.
Câu 15. Tìm tất cả các giá trị của tham số
m
để hàm số
cos2
y x mx
đồng biến trên
.
A.
2
m
. B.
2
m
. C.
2 2
m
. D.
2
m
.
Câu 16. Tìm tất cả các giá trị của
m
để hàm số
2
1
x m
y
x
nghịch biến trên từng khoảng xác định của nó.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Câu 17. Cho hàm số
3 2
3 1 4
y x x m x m
1
,
m
là tham số. Tập hợp tất cả các giá trị thực của
m
để hàm
số đã cho nghịch biến trên khoảng
1;1
là
A.
;2

. B.
; 10

. C.
1;
4

. D.
; 10

.
Câu 18. Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
6 4 5
y x x m x
đồng biến trên khoảng
;3

là
A.
; 8

. B.
; 8

. C.
; 5

. D.
5;

.
Câu 19. Có bao nhiêu giá trị nguyên âm của
m
để hàm số
4
1 3
4 2
y x mx
x
đồng biến trên khoảng
0;

.
A. 2. B. 1. C. 3. D. 0.
Câu 20. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
mx
y
x m
nghịch biến trên khoảng
1;
?
A.
5
. B.
3
. C.
2
. D.
4
.
x
y
O
1
-3
-1
1
5
5. Xét sự đồng biến, nghịch biến của hàm số khi biết đồ thị hoặc bảng biến thiên của hàm đạo hàm.
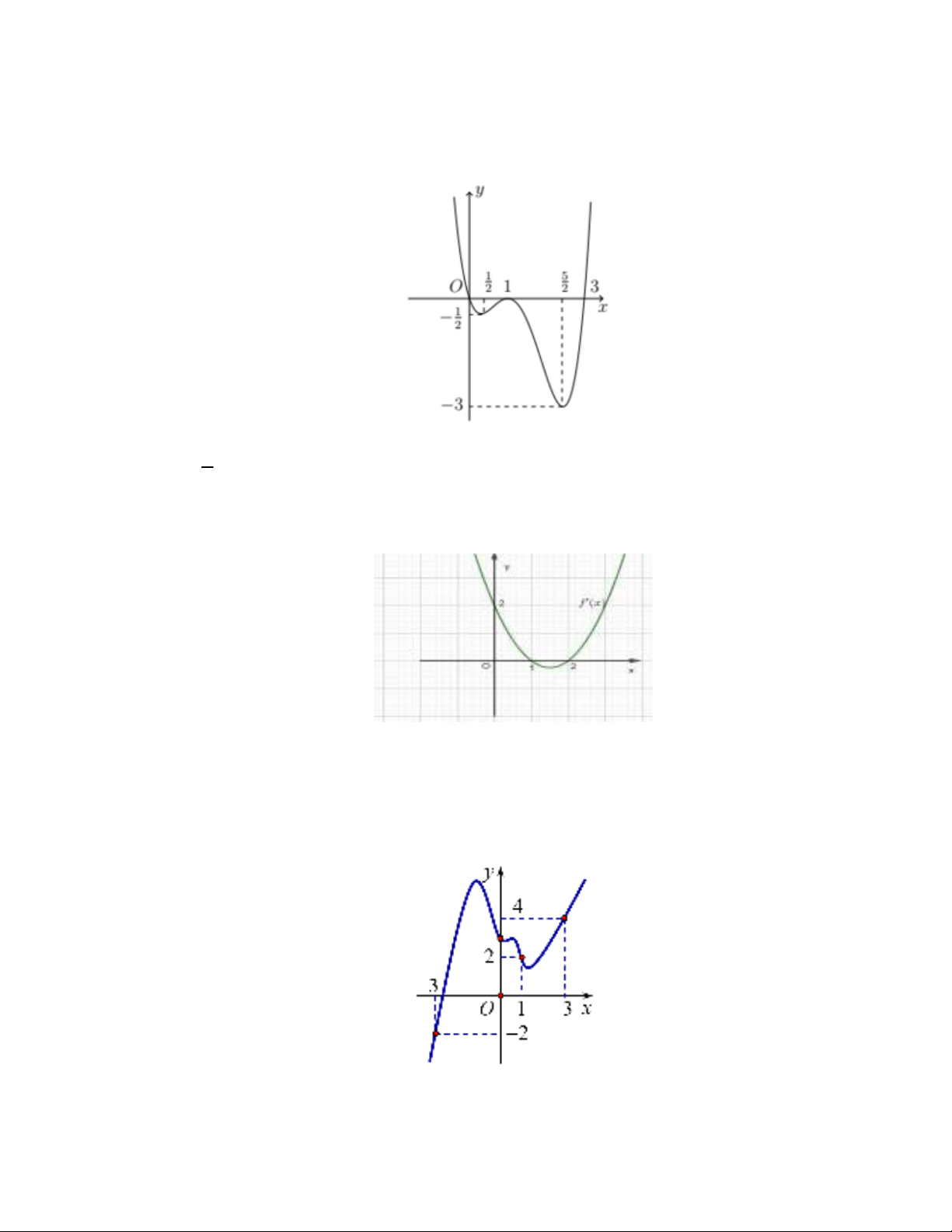
Câu 21. Cho hàm số
y f x
có đạo hàm
f x
trên khoảng
;
. Đồ thị của hàm số
y f x
như hình
vẽ. Hàm số
y f x
nghịch biến trên khoảng nào trong các khoảng sau?
A.
5
;2

. B.
3;
. C.
0;3
. D.
;0
.
Câu 22. Cho hàm số
'y f x
có đồ thị như hình vẽ
Hàm số
2
2y f x
đồng biến trên khoảng nào dưới đây
A.
;0
. B.
0;1
. C.
1;2
. D.
0;
.
Câu 23. Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ.