PHÒNG GIÁO DỤC THÀNH PHỐ BÀ RỊA
TRƯỜNG THCS PHƯỚC HƯNG
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I – NĂM HỌC 2024-2025
MÔN : TOÁN 9
I– NỘI DUNG KIỂM TRA.
Gồm các chủ đề trong chương trình Toán 9 tập 1, cụ thể như sau :
+ Chủ đề 1 : Phương trình và hệ phương trình.
- Giải được giải phương trình tích dạng
(
)
(
)
(
)
0 0, 0
ax b cx d a b
+ + = ≠ ≠
- Giải được phương trình chứa ẩn ở mẫu quy về phương trình bậc nhất.
- Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng hoăc thế.
- Giải được phương trình chứa ẩn ở mẫu
- Giải được bài toán bằng cách lập hệ phương trinh (dạng toán Có nội dung hình học-hình
chữ nhật, chuyển động đơn giản, tỉ lệ phần trăm)
+ Chủ đề 2 : Bất đẳng thức, bất phương trình.
- Biết định nghĩa và một số tính chất cơ bản của bất đẳng thức.
- Biết cách giải bất phương trình bậc nhất.
+ Chủ đề 3 : Căn thức.
- Nắm được định nghĩa, điều kiện xác định biểu thức chứa căn.
- Biết cách tính toán giá trị biểu thức chứa căn.
+ Chủ đề 4 : Hệ thức lượng trong tam giác vuống.
- Biết định nghĩa tỉ số lượng giác góc nhọn
- Nắm được hệ thức liên quan giữa cạnh, góc trong tam giác vuông.
- Giải quyết được một số vấn đề thực tiễn gắn với tỉ số lượng giác của góc nhọn (ví dụ:
Tính độ dài đoạn thẳng, độ lớn góc và áp dụng giải tam giác vuông,...).
+ Chủ đề 5 : Đường tròn.
- Biết định nghĩa đường tròn, dây cung, tiếp tuyến.
- Nắm được các loại góc trong đường tròn (góc ở tâm, góc nội tiếp).
- Nhận diện được 4 điểm cùng thuộc 1 đường tròn trong trường hợp đơn giản.
II- QUI ĐỊNH CHUNG
1. Hình thức kiểm tra: Tự luận
2. Thời gian làm bài kiểm tra: 90 phút.
III – KHUNG MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KỲ I – LỚP 9
Chương
Chủ đề
Nội dung/đơn vị kiến thức
Mức độ đánh giá Tổng
%
điểm
Nhận
biết
Thông
hiểu
Vận
dụng
Vận
dụng cao
Phương trình và
hệ hai phương
trình bậc nhất hai
ẩn
Khái niệm phương trình và hệ
hai phương trình bậc nhất hai ẩn
Phương trình quy về phương
trình b
2
0,5
4
2,0 Giải hệ hai phương trình bậc
nhất hai ẩn 1
0,5
Giải bài toán bằng cách lập hệ
phương trình 1
1,0
Bất phương trình
bậc nhất một ẩn
Bất đẳng thức và tính chất 2
0,5 1
0,5 5
2,0
Bất phương trình bậc nhất một
ẩn
1
0,5
1
0,5
Căn bậc hai và
căn bậc ba
Căn bậc hai và căn thức bậc hai 3
1,0
1
0,5 4
2,5
Căn bậc ba và căn thức bậc ba 2
0,5
1
0,5
Hệ thức lượng
trong tam giác
vuông
Tỉ số lượng giác của góc nhọn 2
1,0
1
0,5 1
0,5
4
2,0
Đường tròn Đường tròn
Tiếp tuyến của đường tròn
1
0,5 2
1,0 3
1,5
Tổng số câu
Điểm
11
4,0
7
3,0
2
2,0
2
1,0
22
10,0
Tỉ lệ % 40% 30% 20% 10% 100%
Tỉ lệ chung 70% 30% 100%
IV-. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA
Chương/
Chủ đề
Nội dung/Đơn vị
kiến thức Mức độ đánh giá
Số câu hỏi theo mức độ nhận
thức
Nhận
Biết
Thông
hiểu
Vận
dụng
Vận
dụng
cao
Phương
trình và hệ
hai phương
Khái niệm
phương trình và
hệ hai phương
– Nhận biết được khái niệm
phương trình bậc nhất hai ẩn,
2
trình bậc
nhất hai ẩn
trình bậc nhất hai
ẩn
Phương trình quy
về phương trình
bậc nhất một ẩn
Giải hệ hai
phương trình bậc
nhất hai ẩn
hệ hai phương trình bậc nhất
hai ẩn.
– Nhận biết được khái niệm
nghiệm của hệ hai phương
trình bậc nhất
hai ẩn.
- Hiểu được cách giải phương
trình tích.
- Hiểu cách giải được hệ hai
phương trình bậc nhất hai ẩn.
1
Giải bài toán
bằng cách lập hệ
phương trình
- Vận dụng, giải thích được
cách thức giải quyết vấn đề về
phương diện học toán.
1
Bất phương
trình bậc
nhất một ẩn
Bất đẳng thức và
tính chất
Bất phương trình
bậc nhất một ẩn
- Phát biểu được khái niệm bất
phương trình bậc nhất một ẩn,
khái niệm nghiệm của bất
phương trình bậc nhất một ẩn.
- Hiểu: Mô tả được một số tính
chất cơ bản của bất đẳng thức
(tính chất bắc cầu; liên hệ giữa
thứ tự và phép cộng, phép
nhân).
- Vận dụng: Vận dụng linh
hoạt kiến thức bất đẳng thức để
tìm giá trị lớn nhất của biểu
thức.
2
1
Căn bậc hai
và căn bậc
ba
Căn bậc hai và
căn thức bậc hai
Biến đổi đơn giản
và rút gọn biểu
thức chứa căn
thức bậc hai
- Hiểu được cách tìm điều kiện
của căn thức bậc hai.
1
1
- Sử dụng được các kiến thức
về phép biến đổi căn thức bậc
hai để rút gọn được biểu thức
chứa căn bậc hai.
3
1
Căn bậc ba và căn
thức bậc ba
- Hiểu được định nghĩa căn bậc
ba để tính giá trị biểu thức số
với căn bậc ba
2
1
Hệ thức
lượng trong
tam giác
vuông
Tỉ số lượng giác
của góc nhọn
Hiểu: - Giải thích được một số
hệ thức về cạnh và góc trong
tam giác vuông, định nghĩa tỉ
số lượng giác của góc nhọn
trong tam giác vuông.
- Lựa chọn được cách thức tính
chiều cao của vật thể trên hình
minh họa có sẵn.
2
1
1
- Xác định được mô hình toán
học cho tình huống xuất hiện
trong bài toán thực tiễn để tính
góc theo yêu cầu.
Đường tròn Đường tròn
Tiếp tuyến của
đường tròn
Giải thích được tiếp tuyến của
đường tròn 1
0,5 2
1,0
Tổng số câu 11 7 2 2
Tỉ lệ % 40% 30% 20% 10%
Tỉ lệ chung 70% 30%
V. ĐỀ THAM KHẢO
ĐỀ 1
Bài 1 (1,0 điểm).
1. Cho 2 số
,
a b
biết
a b
<
. So sánh
a)
5 5
a b
+ +
□
b)
2 2
a b
− −
□
2. Giải bất phương trình sau:
(
)
6 9 6 2 1 .
x x
+ ≥ − −
Bài 2 (2,0 điểm).
1. Tính a)
125
5
b)
3 3
3. 9
2. Rút gọn biểu thức
a)
20 45 5
+ +
b)
(
)
(
)
2 2
3 6 6 3
+ + −
Bài 3 ( 2,5 điểm).
1. Giải các phương trình sau :
a)
(
)
(
)
0.
3 2 4 5
x x
=
− +
b)
(
)
.
2 2 3
2 2
x x
xx
+ +
=−
2. Giải hệ phương trình sau:
3 3
2 8
.
x y
x y
− =
+ =
3. Giải bài toán sau bằng cách lập hệ phương rình:
Một hình chữ nhật có chu vi
150
m
. Nếu tăng chiều rộng thêm
6
m
và giảm chiều dài
15
m
thì hình chữ nhật trở thành hình vuông. Tính tính diện tích khu vườn lúc đầu.
Bài 4 (2,0 điểm) Cho hình bên, biết
AmB
có số đo là
o
60
.
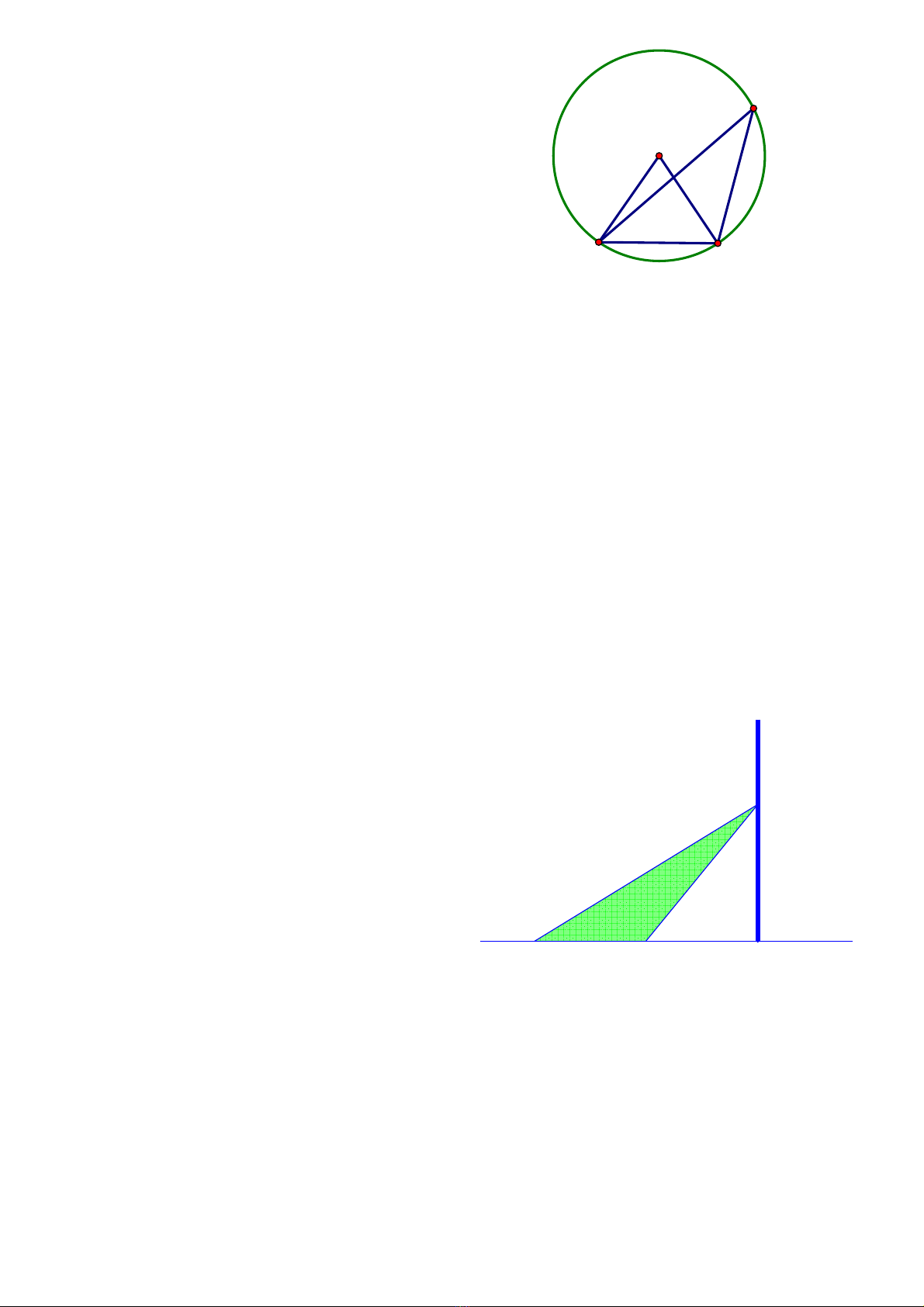
a) Tính số đo góc ở tâm
AOB
b) Tính số đo góc nội tiếp đỉnh
ACB
2.
Cho tam giác
ABC
vuông tại
A
, biết
20
BC cm
=
,
0
35
C
=
.
a) Tính độ dài cạnh
,
AB AC
(làm tròn kết quả lấy 1 chữ số thập phân).
b) Kẻ đường cao
(
)
AH H BC
∈
. Chứng minh
2
.
AB BH BC
=
.
Bài 5 (2,0 điểm).
Cho đường tròn
(
)
,
O R
đường kính
AB
và một dây
AC
không đi qua tâm
O
. Vẽ
OH
vuông
góc với
AC
.
1) Chứng minh
OH
song song với
BC
.
2) Tiếp tuyến tại
A
C của đường tròn
(
)
O
cắt
OH
tại
M
. Chứng minh
MA
là tiếp
tuyến của đường tròn
(
)
O
.
Bài 6 (0,5 điểm).
Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng
triển lãm. Thiết bị này có góc chiếu sáng là
0
20
và cần đặt cao hơn mặt đất là
2,5
m
.
Người ta đặt thiết bị này sát tường và canh
chỉnh sao cho trên mặt đất dải ánh sáng bắt
đầu từ vị trí cách tường
2
m
. Hãy tính độ
dài vùng được chiếu sáng trên mặt đất.
ĐỀ 2
Bài 1 (1,0 điểm).
1
. Cho 2 số
,
a b
biết
a b
≥
. So sánh
a)
3 3
a b
□
b)
7 7
a b
− −
□
2.
Giải bất phương trình sau:
4 1 2 6 3 5 2
x x
m
O
AB
C
2m?m
2,5m
thiết bị chiếu sáng
bức tường
dải ánh sáng